充分必要条件

贡献者：叶燊Leafshen; addis

预备知识　集合（高中）

未完成：另开词条

1. 韦恩图

　　 韦恩图（Veen diagram），是在所谓的集合论（或者类的理论）数学分支中，在不太严格的意义下用以表示集合（或类）的一种草图。它们用于展示在不同的事物群组（集合）之间的数学或逻辑联系，尤其适合用来表示集合（或）类之间的 “大致关系”。它也常常被用来帮助推导（或理解推导过程）关于集合运算（或类运算）的一些规律。

图 1：Veen 图

　　条件越多，在韦恩图上范围就越小，这似乎很好理解。

　　我们将全集用黄色来表示，一个个限制条件瓦解侵蚀，我们用粉色来标记。那么，如图所示：

图 2：条件越多，在韦恩图上范围就越小

2. 学科联系

　　在语文逻辑中，我们这样解释： “马” 是一类事物的总称。限制条件诸如 “高大的”“白色的”“会飞的” 等等，具体了其内涵，缩小了其外延。

　　概念的内涵就是指反映在概念中的对象的本质属性或特有属性。

　　概念的外延是指具有概念所反映的本质属性或特有属性的对象，即概念的适用范围。

　　两者的区别：

　　 1. 本质不同：内涵是 “属性”，外延是 “范围”。属性越多，则符合这个属性的范围越小。属性越少，符合这个属性的范围就越大。

　　 2. 侧重不同：概念的内涵是指概念的质的方面。概念的外延是指概念的量的方面。

　　若由命题 $A$ 能推导出命题 $B$，则 $A$ 是 $B$ 的充分条件，$B$ 是 $A$ 的必要条件。如何理解这个定义呢？下面举两个例子。

例 1　

　　命题 $A$：四边形 $ABCD$ 是一个正方形。

　　命题 $B$：四边形 $ABCD$ 的四条边相等。

　　首先我们考虑 $A$ 对 $B$ 的关系。显然，由 $A$ 可以推出 $B$，说明 $A$ 中有充分的信息能得到 $B$，所以叫做 $B$ 的充分条件。$A$ 中包括得到 $B$ 所必要的信息，还可能包括一些其他信息，例如由命题 $A$ 可以得出四边形任意两条临边垂直。这些多出来的信息并不一定是得到 $B$ 所必须的，因为还有许多其他的四边形四条边相等但并不是正方形。

　　那如何判断 $A$ 中有没有多余的信息呢？我们可以反过来试图用 $B$ 推导命题 $A$，若原则上得不出 $A$（而不是因为我们逻辑水平不够），则证明 $A$ 中有多余的条件。这时我们说 $A$ 不是 $B$ 的必要条件，因为 $A$ 中的一些信息是多余的，也就是没有必要的。综上，$A$ 是 $B$ 的充分非必要条件。

　　现在我们从 $B$ 的角度考虑。虽然由条件 $B$ 不能推导出条件 $A$，但是 $B$ 是 $A$ 中信息的一部分，$B$ 必须要成立才有可能使 $A$ 成立，也就是说如果 $B$ 不成立 $A$ 就不可能成立（四条边不全相等的四边形一定不是正方形）。所以说 $B$ 是 $A$ 的必要条件。另外，由 $B$ 中的少量信息不能得到 $A$，所以 $B$ 不是 $A$ 的充分条件。综上，$B$ 是 $A$ 的必要非充分条件。

例 2　

　　命题 $A$：三角形 $X$ 的其中两内个角分别为 $90^\circ$ 和 $45^\circ$。

　　命题 $B$：三角形 $X$ 有两个 $45^\circ$ 的内角。

　　利用三角形三个内角和为 $180^\circ$ 的事实，可以从 $A$ 推出 $B$，说明 $A$ 是 $B$ 的充分条件，$B$ 是 $A$ 的必要条件。但也可以从 $B$ 推出 $A$，说明 $B$ 是 $A$ 的充分条件，$A$ 是 $B$ 的必要条件。所以 $A$ 和 $B$ 既是彼此的充分条件也是彼此的必要条件。所以我们说 $A$ 和 $B$ 互为充分必要条件。若 $A$ 是 $B$ 的充分必要条件，$B$ 一定也是 $A$ 的充分必要条件。因为两种表述都意味着 $A$， $B$ 命题等效，所提供的信息都是一样的，两者都没有任何多余的或者缺失的信息。

　　需要注意的是：

充分/必要条件是两个命题之间的关系，若直说一个命题是充分/必要条件没有意义。
讨论充分/必要条件需要在一定的前提下进行。以上两个例子中的前提如：我们讨论的是欧几里得几何中的平面四边形和三角形。当然，我们也可以把这个前提直接写在每个命题中。
在证明 $A$ 是 $B$ 的充分必要条件时，需要分别证明 $A$（相对于 $B$）的充分性和必要性。充分性需要由 $A$ 证明 $B$，必要性需要由 $B$ 证明 $A$。
在证明 $A$ 是 $B$ 的充分非必要条件时，除了需要证明 $A$ 的充分性，还需非必要性，即 $B$ 不能推出 $A$。只要我们可以举出一个 $B$ 成立 $A$ 不成立的反例，就立刻证明了不可能由 $B$ 推出 $A$。

　　简要说明：

　　有命题 $A$ 和 $B$

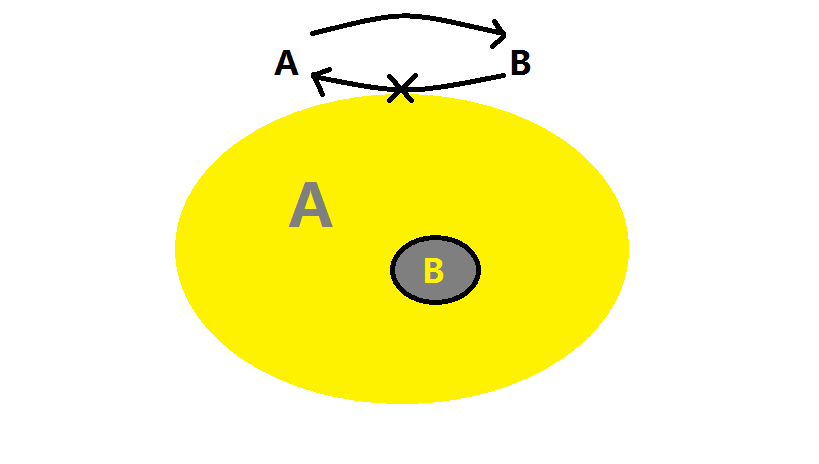
$A$ 推出 $B$，$B$ 推不出 $A$，则为充分不必要，如图：

图 3：充分不必要
口诀：有之必然，无之未必不然
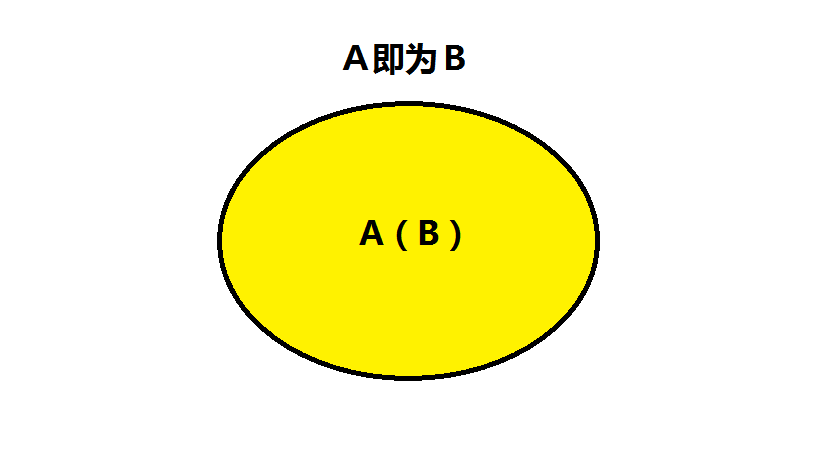
$A$ 推出 $B$，$B$ 推出 $A$，则为充要，如图：

图 4：充要
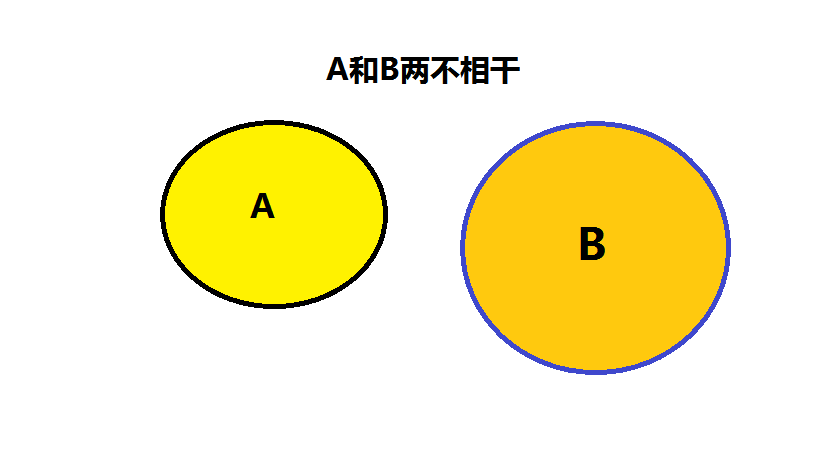
$A$ 推不出 $B$，$B$ 推不出 $A$，则既不充分也不必要，如图：

图 5：既不充分也不必要
$A$ 推不出 $B$，$B$ 推出 $A$，则必要不充分，如图：

图 6：必要不充分
口诀：有之未必然，无之必不然