贡献者: 待更新
如果我们要测量线偏振的超快激光脉冲的波形(即电场关于时间的函数),我们不能直接用仪器测量,因为电子元件的时间分辨率远远不够。但我们可以使用 Frequency Resolved Optical Gating(FROG)。FROG 有许多不同的实现方法,这里只讨论比较常见的 SHG FROG(Second Harmonic Generation FROG)和 PCGPA。
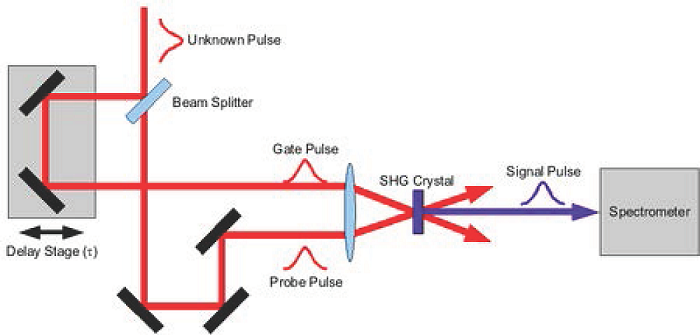
图 1:SHG FROG 的光路(图片来自 WikiPedia)
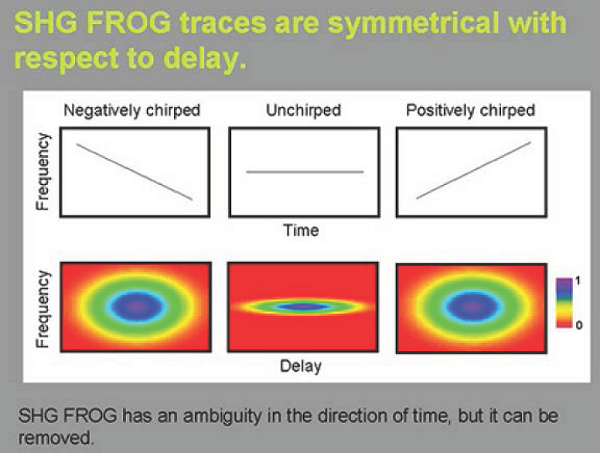
图 2:SHG FROG trace(图片来自网络)
Frog 的大概原理就是把被测量的脉冲(prob)$f(t)$ 和另一个脉冲(gate)$g(t)$ 叠加(注意 $f(t)$ 和 $g(t)$ 都是实函数),然后通过一个二阶非线性介质产生一个 $f(t)g(t)$ 脉冲并分离出来,再测量光谱(即傅里叶变换)。接下来我们可以控制两个脉冲的相对延迟(time delay)$\tau$,就得到不同延迟下 $f(t - \tau)g(t)$ 的光谱,也就是一个二维函数,叫做 FROG trace(图 2 )。很多情况下,gate 就是 prob 通过一个 beam splitter 分出来的,实验光路如图 1 所示。
\begin{equation}
a(\omega, \tau) = \left\lvert \int_{-\infty}^{\infty} f(t-\tau) g(t) \mathrm{e} ^{- \mathrm{i} \omega t} \,\mathrm{d}{t} \right\rvert ^2~.
\end{equation}
只要用特定的算法,就可以从
式 1 中解出 $f(t)$ 和 $g(t)$。
1. PCGPA 算法
PCGPA(Principal Component General Projection Algorithm)就是从式 1 中解出 $f(t)$ 和 $g(t)$ 的一种常见算法。在得到 我们假设 $f(t)$ 和 $g(t)$ 都是等时间间隔的离散点 $f_1, f_2\dots, f_N$ 和 $g_2, g_2\dots, g_N$,可以看成两个列矢量。我们先来做两矢量的外积,即
\begin{equation}
\boldsymbol{\mathbf{f}} \boldsymbol{\mathbf{g}} ^{\mathrm{T}} = \begin{pmatrix}
f_1g_1 & \ldots & f_1g_N\\
\vdots & \ddots & \vdots\\
f_Ng_1 & \ldots & f_Ng_N\end{pmatrix} ~.
\end{equation}
然后我们把第 $i$ 行向左移动 $i-1$ 个元(左边多出的矩阵元补到右边),得到
\begin{equation}
\begin{pmatrix}
f_1g_1 & f_1g_2 & \ldots & f_1g_N\\
f_2g_2 & f_2g_3 & \ldots & f_2g_1\\
\vdots & \vdots & \vdots & \vdots\\
f_Ng_N & f_Ng_1 & \ldots & f_Ng_{N-1}
\end{pmatrix} ~.\end{equation}
现在可以发现每一列恰好是 $f(t-\tau)g(t)$ 的离散形式
1,第 $i$ 列 $\tau = (i - 1)\Delta t$。然而当 $i > N/2$ 的时候,更自然的理解是 $\tau = (i-N)\Delta t$。例如与其认为第 $N$ 列是 $g$ 向上移动了 $N-1$ 个元,倒不如认为是向下移动了 $1$ 个元。根据这种思想,我们可以把矩阵左半和右半调换得到
\begin{equation}
\begin{pmatrix}
f_1g_{N/2 + 1} & f_1g_{N/2+2} & \ldots & f_1g_{N/2}\\
f_2g_{N/2 + 2} & f_2g_{N/2+3} & \ldots & f_2g_{N/2+1}\\
\vdots & \vdots & \vdots & \vdots\\
f_Ng_{N/2} & f_Ng_{N/2+1} & \ldots & f_Ng_{N/2-1}
\end{pmatrix} ~.\end{equation}
这样,从左到右的每列分别对应从 $\tau = -(N/2)\Delta t, \dots, (N/2 - 1)\Delta t$。
现在我们对每一列做离散傅里叶变换(注意前后都要 fftshift),就得到了含相位的 Frog trace 矩阵,其中的每一列都是式 1 中的
\begin{equation}
\int_{-\infty}^{\infty} f(t-\tau) g(t) \mathrm{e} ^{- \mathrm{i} \omega t} \,\mathrm{d}{t} ~.
\end{equation}
1. ^ 唯一的区别是从最上面移出的 $g_i$ 跑到了最下面,而在实验中最下面应该由 0 来填补。但如果 $ \boldsymbol{\mathbf{f}} $ 和 $ \boldsymbol{\mathbf{g}} $ 矢量的首尾都有足够多的 0,这个问题就自动解决了。