贡献者: addis; 零穹; ACertainUser
预备知识 电流产生磁场
,电流密度
,矢量叉乘
,线积分
1. 闭合回路的磁场
若已知空间中的电流分布,毕奥—萨伐尔定律(Biot–Savart law)给出了这些电流产生的磁场。我们先讨论一种较为简单的情况,即一根粗细可忽略的闭合导线中的恒定电流产生的磁场1。假设导线中电流为 $I$,空间中任意位置 $ \boldsymbol{\mathbf{r}} $ 的磁场可以用线积分表示为
\begin{equation}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) = \frac{\mu_0}{4\pi} \oint \frac{I \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} \boldsymbol\times \hat{\boldsymbol{\mathbf{R}}} }{R^2}
= \frac{\mu_0}{4\pi} \oint \frac{I \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} \boldsymbol\times ( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ')}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert ^3}~.
\end{equation}
其中积分路径是导线所在的环路,延某个指定的正方向进行。如果电流也是沿正方向,那么 $I$ 大于零,否则小于零。$ \boldsymbol{\mathbf{r}} '$ 是导线上某点的位置,矢量 $ \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} $ 代表导线上的一小段的长度和方向。$ \boldsymbol{\mathbf{R}} = \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} '$,$ \hat{\boldsymbol{\mathbf{R}}} = \boldsymbol{\mathbf{R}} /R$ 表示 $ \boldsymbol{\mathbf{R}} $ 的单位矢量,$R = \left\lvert \boldsymbol{\mathbf{R}} \right\rvert $ 是模长。如果有多个这样的闭合导线,可以分别计算它们的磁场并叠加即可。
使用这个公式需要注意两点。第一,电流及其分布不随时间变化。这点可以从 “不存在瞬时作用” 理解,假设某时刻电流突然从 0 变为某个值,由于电磁场传播需要一定时间,环路上不可能瞬间出现磁场。第二,磁场不仅可以由电流产生,变化的电场也会产生磁场。
毕奥—萨伐尔定律精确符合麦克斯韦方程组,不存在近似。
电流密度形式
更一般地,若电流分布以电流密度 $ \boldsymbol{\mathbf{j}} ( \boldsymbol{\mathbf{r}} )$ 来描述,那么
\begin{equation}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) = \frac{\mu_0}{4\pi} \int \frac{ \boldsymbol{\mathbf{j}} ( \boldsymbol{\mathbf{r}} ') \boldsymbol\times \hat{\boldsymbol{\mathbf{R}}} }{R^2} \,\mathrm{d}{V'} = \frac{\mu_0}{4\pi} \int \frac{ \boldsymbol{\mathbf{j}} ( \boldsymbol{\mathbf{r}} ') \boldsymbol\times ( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ')}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert ^3} \,\mathrm{d}{V'} ~,
\end{equation}
其中 $\int \dots \,\mathrm{d}{V'} $ 表示对 $ \boldsymbol{\mathbf{r}} '$ 在整个三维空间积分(或者包含所有电流的有限空间)。
旋度形式
式 1 和式 2 的另一种等价形式为
\begin{equation}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) = \frac{\mu_0}{4\pi} \boldsymbol{\nabla}\boldsymbol{\times} \oint \frac{I}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert } \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} ~,
\end{equation}
\begin{equation}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) = \frac{\mu_0}{4\pi} \boldsymbol{\nabla}\boldsymbol{\times} \int \frac{ \boldsymbol{\mathbf{j}} ( \boldsymbol{\mathbf{r}} ')}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert } \,\mathrm{d}{V'} ~.
\end{equation}
推导见下文,这在一些情况下反而计算更方便。另外,这也可以用来推导已知电流分布产生的
磁矢势。
矢量积分的计算方法
毕奥—萨伐尔定律的积分中含有矢量微元的叉乘,看起来和普通的矢量积分不同,但是在常见的简单问题中,可以从叉乘的几何意义上直接转换为标量的积分(例 1 和例 2 )。如果是更一般的问题,则可以把叉乘分解成 3 个分量,然后变为 6 个标量积分
\begin{equation} \begin{aligned}
\,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} \boldsymbol\times \boldsymbol{\mathbf{R}} &=
\begin{vmatrix}
\hat{\boldsymbol{\mathbf{x}}} & \hat{\boldsymbol{\mathbf{y}}} & \hat{\boldsymbol{\mathbf{z}}} \\
\,\mathrm{d}{x'} & \,\mathrm{d}{y'} & \,\mathrm{d}{z'} \\
x - x' & y - y' & z - z'
\end{vmatrix}\\
&= \hat{\boldsymbol{\mathbf{x}}} [(z - z') \,\mathrm{d}{y'} - (y - y') \,\mathrm{d}{z'} ] + \hat{\boldsymbol{\mathbf{y}}} [\dots] + \hat{\boldsymbol{\mathbf{z}}} [\dots]~,
\end{aligned} \end{equation}
\begin{equation} \begin{aligned}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) &= \frac{\mu_0}{4\pi} \oint \frac{I \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} \boldsymbol\times \hat{\boldsymbol{\mathbf{R}}} }{R^2}
= \frac{\mu_0 I}{4\pi} \oint \frac{ \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} \boldsymbol\times \boldsymbol{\mathbf{R}} }{R^3} \\
& = \hat{\boldsymbol{\mathbf{x}}} \frac{\mu_0 I}{4\pi} \left[\oint \frac{1}{R^3} (z - z') \,\mathrm{d}{y'} - \oint \frac{1}{R^3} (y - y') \,\mathrm{d}{z'} \right] + \hat{\boldsymbol{\mathbf{y}}} [\dots] + \hat{\boldsymbol{\mathbf{z}}} [\dots]~.
\end{aligned} \end{equation}
例 1 无限长直导线的磁场
图 1:无限长直导线的磁场
如图 1 ,令导线与 $x$ 轴重合,并使原点到场点的距离最近,有 $x = r\tan\theta$,微分得 $ \left\lvert \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} \right\rvert = \,\mathrm{d}{x} = r\sec^2\theta \,\mathrm{d}{\theta} $,另有 $ \hat{\boldsymbol{\mathbf{x}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{R}}} = \hat{\boldsymbol{\mathbf{z}}} \sin\left(\theta + \pi/2\right) = \hat{\boldsymbol{\mathbf{z}}} \cos\theta $,$R = r/\cos\theta$。代入式 1 得
\begin{equation}
\boldsymbol{\mathbf{B}} = \frac{\mu_0}{4\pi} I \hat{\boldsymbol{\mathbf{z}}} \int_{-\pi/2}^{\pi/2} \frac{(r \sec^2\theta \,\mathrm{d}{\theta} ) \cos\theta}{r^2/\cos\theta^2}
= \frac{\mu_0}{4\pi} \frac Ir \hat{\boldsymbol{\mathbf{z}}} \int_{-\pi/2}^{\pi/2} \cos\theta \,\mathrm{d}{\theta}
= \frac{\mu_0}{2\pi} \frac Ir \hat{\boldsymbol{\mathbf{z}}} ~.
\end{equation}
可见磁场大小与距离 $r$ 成反比,总是垂直于导线,且方向符合右手定则。
例 2 环形电流轴线的磁场
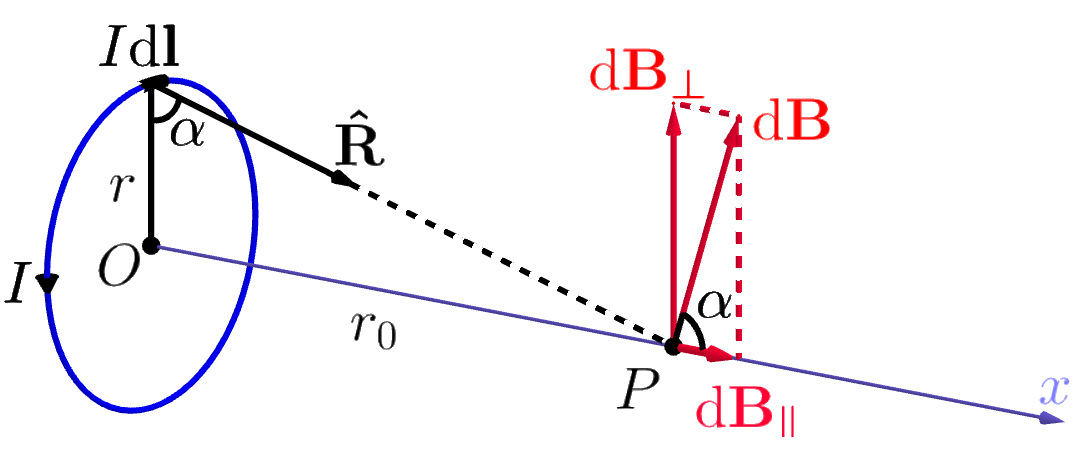
图 2:环形电流轴线上的磁场
如图 2 ,电流环半径为 $r$,以电流环圆心为原点,垂直与环面的轴线为 $x$ 轴,在轴线上任取一点 $P$,其与 $O$ 点距离 $r_0$,令 $P$ 点与电流元 $I\mathrm{d} \boldsymbol{\mathbf{l}} $ 的连线与环面夹角为 $\alpha$, 则电流元 $I\mathrm{d} \boldsymbol{\mathbf{l}} $ 在 $P$ 点的磁场为
\begin{equation}
\mathrm{d}\boldsymbol{B}=\frac{\mu_0}{4\pi}\frac{I\mathrm{d} \boldsymbol{\mathbf{l}} \times\hat{ \boldsymbol{\mathbf{R}} }}{R^2}~.
\end{equation}
从几何关系知道,$\mathrm{d} \boldsymbol{\mathbf{B}} $ 在 $x$ 轴与 $ \boldsymbol{\mathbf{R}} $ 所在直线组成的平面内,且与 $x$ 轴夹角为 $\alpha$,将 $\mathrm{d} \boldsymbol{\mathbf{B}} $ 分解为平行于 $x$ 轴 的分量 $\mathrm{d}\boldsymbol{B_\parallel}$ 和垂直于 $x$ 轴的分量 $\mathrm{d} \boldsymbol{\mathbf{B_\bot}} $. 由对称性可知,电流环上与电流元 $I\mathrm{d} \boldsymbol{\mathbf{l}} $ 关于圆心 $O$ 中心对称的电流元 $I\mathrm{d} \boldsymbol{\mathbf{l'}} $ 在 $P$ 点的磁场垂直分量必定与 $\mathrm{d} \boldsymbol{\mathbf{B_\bot}} $ 等大反向。于是,所有电流元在 $P$ 点的磁场垂直分量的矢量和为零。那么,由式 2
\begin{equation}
\begin{aligned}
\boldsymbol{\mathbf{B}} &=\oint{\mathrm{d} \boldsymbol{\mathbf{B_\parallel}} }=\oint\mathrm{d}B\cos{\alpha} \hat{\boldsymbol{\mathbf{x}}} =\oint\frac{\mu_0}{4\pi}\frac{I\mathrm{d}l}{R^2}\cos\alpha \hat{\boldsymbol{\mathbf{x}}} \\
&=\frac{\mu_0Ir}{2R^2}\cos\alpha=\frac{\mu_0Ir^2}{2R^3} \hat{\boldsymbol{\mathbf{x}}} \\
&=\frac{\mu_0Ir^2}{2(r_0^2+r^2)^{\frac{3}{2}}} \hat{\boldsymbol{\mathbf{x}}} ~.
\end{aligned}
\end{equation}
2. 详细说明
毕奥—萨伐尔定律是电磁学的基本假设之一2,所以以下并不是推导,而是解释公式的意义。
一个粗细忽略不计的电流回路中有电流 $I$,如何确定该回路在空间中任意一点所产生的磁场呢?由于磁场与电场一样可以叠加,我们可以把回路划分成极小的线段,分别计算每个小线段在某点 $ \boldsymbol{\mathbf{r}} $ 产生的磁场,然后求和。当这些小线段的长度趋近于零,求和就变成了线积分。
图 3:$ \boldsymbol{\mathbf{r}} '$ 处的一小段电流 $I \,\mathrm{d}{ \boldsymbol{\mathbf{}}} r'$ 在 $ \boldsymbol{\mathbf{r}} $ 处产生磁场 $ \,\mathrm{d}{ \boldsymbol{\mathbf{}}} B$.
那如何计算一小段(电流元)产生的磁场呢?令该电流元位置为 $ \boldsymbol{\mathbf{r}} '$,长度为 $ \,\mathrm{d}{r} $,为了标明正方向可以记为矢量微元 $ \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } $。现在我们要求空间中任意一点 $ \boldsymbol{\mathbf{r}} $(把这点叫做场点)的磁场,设电流元的位置为 $ \boldsymbol{\mathbf{r}} $(把这点叫做原点),且设
\begin{equation}
\boldsymbol{\mathbf{R}} = \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} '~,
\end{equation}
令 $ \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } $ 与 $ \boldsymbol{\mathbf{R}} $ 的夹角为 $\theta$。
首先,磁场大小正比于 $I$,这是合理的,因为如果把两小段电流元重叠放在一起,那么根据叠加原理,任何地方的磁场都会增加一倍。其次,与点电荷的电场(库仑定律)类似,场强与距离的平方成反比。最后,由于电流有特定的方向,磁场不再具有球对称性,而是以导线为轴的中心对称。磁场大小正比于 $ \left\lvert \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } \boldsymbol\times \hat{\boldsymbol{\mathbf{R}}} \right\rvert = \sin\theta \,\mathrm{d}{r} $(磁场方向垂直于 $ \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } $ 和 $ \boldsymbol{\mathbf{R}} $ 所在平面,符合右手定则,见 “叉乘”)。这说明,在 $I, \boldsymbol{\mathbf{r}} '$ 和长度 $R$ 不变时,该电流源在垂直它的方向($\theta = \pi /2$)产生最大场强,在共线方向($\theta = 0$)场强为零。
要注意的是,虽然我们是对单独一个 $I \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } $ 分析,但稳定的单个电流元在现实中并不存在。因为线电流必须组成环路,否则在两个端点处就会分别积累大量的异号电荷(见电流的连续性),从而产生变化的电场及磁场,而在静态电磁场问题中,我们要求净电荷和电流的分布不随时间改变。所以在利用毕奥—萨伐尔定律时,必须要以对整个闭合回路积分(无穷长直导线或者螺线管等理想化问题除外)若给所有的小电流源编号为 $I \,\mathrm{d}{ \boldsymbol{\mathbf{r}} _i} $,令第 $i$ 个电流源的起点为 $ \boldsymbol{\mathbf{r}} '_i$,$ \boldsymbol{\mathbf{R}} _i = \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} '_i$。把所有电场矢量相加,变为
\begin{equation}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) = \frac{\mu_0}{4\pi} \sum\limits_i \frac{I \,\mathrm{d}{ \boldsymbol{\mathbf{r}} _i} \boldsymbol\times \hat{\boldsymbol{\mathbf{R}}} _i}{R_i^2}~.
\end{equation}
当电流元无穷短,数量无穷多的时候,上式写为积分的形式,且由于第 $i$ 个电流元的终点就是第 $i+1$ 个电流元的起点,$ \,\mathrm{d}{ \boldsymbol{\mathbf{l}} _i} = \boldsymbol{\mathbf{r}} '_{i + 1} - \boldsymbol{\mathbf{r}} '_i = \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} $,矢量积分写为
\begin{equation}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) = \frac{\mu_0}{4\pi} \oint \frac{I \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} \boldsymbol\times \hat{\boldsymbol{\mathbf{R}}} }{R^2}~.
\end{equation}
注意 $ \boldsymbol{\mathbf{R}} $ 是场点 $ \boldsymbol{\mathbf{r}} $ 和源点 $ \boldsymbol{\mathbf{r}} '$ 的函数,积分时把 $ \boldsymbol{\mathbf{r}} $ 视为常数而对 $ \boldsymbol{\mathbf{r}} '$ 积分。为了使公式更明确,在另一些电磁学教材中把上式直接记为
\begin{equation}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) = \frac{\mu_0}{4\pi} \oint \frac{I \,\mathrm{d}{ \boldsymbol{\mathbf{r}} '} \boldsymbol\times ( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ')}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert ^3}~.
\end{equation}
电流密度的形式
这里使用一个简单的例子把毕奥—萨伐尔定律拓展到任意电流密度分布 $ \boldsymbol{\mathbf{j}} $ 的情况(注意不是推导)。事实上这才是更一般的毕奥—萨伐尔定律,前者可以看成是一种特殊情况。
假设电流的空间分布是连续变化的而不能看成一条截面不计曲线,我们需要用电流密度 $ \boldsymbol{\mathbf{j}} $ 来表示空间的电流分布。现在考虑一个粗细不能忽略的环路,$ \boldsymbol{\mathbf{r}} '$ 处的截面积为 $A$(取截面时应垂直于电流),通过截面的电流为 $I = A \boldsymbol{\mathbf{j}} $,所以电流元变为 $I \,\mathrm{d}{ \boldsymbol{\mathbf{l}} } = \boldsymbol{\mathbf{J}} A \,\mathrm{d}{l} = \boldsymbol{\mathbf{j}} \boldsymbol\cdot \,\mathrm{d}{V} $(根据定义,$ \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } $ 与 $ \boldsymbol{\mathbf{j}} $ 的正方向相同),$ \,\mathrm{d}{V} $ 是电流元的体积。于是毕奥—萨伐尔定律的环路积分变为体积分
\begin{equation}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) = \frac{\mu_0}{4\pi} \int \frac{ \boldsymbol{\mathbf{j}} ( \boldsymbol{\mathbf{r}} ') \boldsymbol\times \hat{\boldsymbol{\mathbf{R}}} }{R^2} \,\mathrm{d}{V'} ~,
\end{equation}
注意积分内的电流密度是关于源点的函数而不是场点的函数。理论上,体积分应该在导线内部进行,然而导线外部电流密度为零,故积分可以对全空间进行。类比
式 13 ,更明确的写法是
\begin{equation}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) = \frac{\mu_0}{4\pi} \int \frac{ \boldsymbol{\mathbf{j}} ( \boldsymbol{\mathbf{r}} ') \boldsymbol\times ( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ')}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert ^3} \,\mathrm{d}{V'} ~,
\end{equation}
积分时 $ \boldsymbol{\mathbf{r}} $ 视为常数。
3. 旋度形式的证明
这里证明式 4 和式 2 等效,式 3 的证明同理(留做习题)。由梯度的定义易得
\begin{equation}
\frac{ \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} '}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert ^3} = - \boldsymbol\nabla \frac{1}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert }~,
\end{equation}
注意这里的 $ \boldsymbol\nabla $ 算符只对 $ \boldsymbol{\mathbf{r}} $ 作用。将其代入
式 2 得
\begin{equation}
\begin{aligned}
\boldsymbol{\mathbf{B}} ( \boldsymbol{\mathbf{r}} ) &= \frac{\mu_0}{4\pi} \int \frac{ \boldsymbol{\mathbf{j}} ( \boldsymbol{\mathbf{r}} ') \boldsymbol\times ( \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ')}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert ^3} \,\mathrm{d}{V'} \\
&= \frac{\mu_0}{4\pi} \int \boldsymbol\nabla \frac{1}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert } \boldsymbol\times \boldsymbol{\mathbf{j}} ( \boldsymbol{\mathbf{r}} ') \,\mathrm{d}{V'} \\
&= \frac{\mu_0}{4\pi} \boldsymbol{\nabla}\boldsymbol{\times} \int \frac{ \boldsymbol{\mathbf{j}} ( \boldsymbol{\mathbf{r}} ')}{ \left\lvert \boldsymbol{\mathbf{r}} - \boldsymbol{\mathbf{r}} ' \right\rvert } \,\mathrm{d}{V'} ~.
\end{aligned}
\end{equation}
最后一步使用了
式 5 ,当 $ \boldsymbol{\mathbf{A}} $ 为常数时
\begin{equation}
( \boldsymbol\nabla f) \boldsymbol\times \boldsymbol{\mathbf{A}} = \boldsymbol{\nabla}\boldsymbol{\times} (f \boldsymbol{\mathbf{A}} )~.
\end{equation}
证毕。
1. ^ 在电动力学中,我们提到不存在瞬间作用,电磁场的传播需要时间。而且变化的磁场也会产生变化的电场,这将使计算变得十分复杂,我们将在 “推迟势” 中介绍。
2. ^ 也可以把麦克斯韦方程组中关于磁场旋度的式子看成基本假设,毕奥—萨伐尔是在静电学条件下的推论。