贡献者: addis; ACertainUser; Giacomo
向量叉乘在物理定律中十分常见,例如在讨论力学中的力矩,角动量,以及电磁学中的洛伦兹力,安培力时都会使用。以下我们讨论的向量都是三维中的空间向量;在讨论它们的坐标时,我们默认取正交归一基底。
1. 叉乘的几何定义
图 1:叉乘的示意图
两个几何向量 $ \boldsymbol{\mathbf{A}} $, $ \boldsymbol{\mathbf{B}} $ 的叉乘(cross product) 也叫叉积,向量积(vector product)或向量积。叉乘的结果是一个向量。 叉乘用 $ \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} $ 表示,且 “$ \boldsymbol\times $” 不可省略。
定义 1 向量叉乘
要确定一个几何向量,只需分别确定模长和方向:
- $ \boldsymbol{\mathbf{C}} $ 的模长等于 $ \boldsymbol{\mathbf{A}} , \boldsymbol{\mathbf{B}} $ 的模长之积与夹角 $\theta$($0 \leqslant \theta \leqslant \pi$)的正弦值相乘。
\begin{equation}
\left\lvert \boldsymbol{\mathbf{C}} \right\rvert = \left\lvert \boldsymbol{\mathbf{A}} \right\rvert \left\lvert \boldsymbol{\mathbf{B}} \right\rvert \sin\theta ~.
\end{equation}
- $ \boldsymbol{\mathbf{C}} $ 的方向垂直于 $ \boldsymbol{\mathbf{A}} , \boldsymbol{\mathbf{B}} $ 所在的平面,且由右手定则决定。
结合图 1 与式 1 ,可看出 $ \boldsymbol{\mathbf{C}} $ 的大小就是 $ \boldsymbol{\mathbf{A}} , \boldsymbol{\mathbf{B}} $ 所围成的平行四边形的面积,亦即用平行四边形法则计算 $ \boldsymbol{\mathbf{A}} + \boldsymbol{\mathbf{B}} $ 时的平行四边形。
2. 叉乘运算律
一个结论
特别地,由式 1 可知,当两向量平行时,叉乘为零向量;当它们垂直,叉乘的模长等于两模长直接相乘。
叉乘的 “交换律”
与内积和数乘不同,叉乘不满足一般意义上的交换律。根据几何定义,$ \boldsymbol{\mathbf{B}} \boldsymbol\times \boldsymbol{\mathbf{A}} $ 与 $ \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} $ 模长相同,方向却相反。表示某个向量的反方向,就是在前面加负号,所以有
\begin{equation}
\boldsymbol{\mathbf{B}} \boldsymbol\times \boldsymbol{\mathbf{A}} = - \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} ~.
\end{equation}
叉乘与数乘的结合律
在 $ \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} = \boldsymbol{\mathbf{C}} $ 中,$ \boldsymbol{\mathbf{C}} $ 的方向仅由 $ \boldsymbol{\mathbf{A}} $ 和 $ \boldsymbol{\mathbf{B}} $ 的方向决定。当 $ \boldsymbol{\mathbf{A}} $ 和 $ \boldsymbol{\mathbf{B}} $ 的方向不变时,$ \boldsymbol{\mathbf{C}} $ 的模长正比于 $ \boldsymbol{\mathbf{A}} $ 和 $ \boldsymbol{\mathbf{B}} $ 的模长之积。假设 $\lambda $ 为常数(标量),显然有
\begin{equation}
(\lambda \boldsymbol{\mathbf{A}} ) \boldsymbol\times \boldsymbol{\mathbf{B}} = \boldsymbol{\mathbf{A}} \boldsymbol\times (\lambda \boldsymbol{\mathbf{B}} ) = \lambda ( \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} )~.
\end{equation}
即标量的位置可以任意变换,但向量与乘号的位置关系始终要保持不变。
叉乘的分配律
叉乘一个最重要的特性,就是它满足分配律。
\begin{equation}
\boldsymbol{\mathbf{A}} \boldsymbol\times ( \boldsymbol{\mathbf{B}} + \boldsymbol{\mathbf{C}} ) = \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} + \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{C}} ~,
\end{equation}
由
式 2 及上式可以推出
\begin{equation}
( \boldsymbol{\mathbf{A}} + \boldsymbol{\mathbf{B}} ) \boldsymbol\times \boldsymbol{\mathbf{C}} = - \boldsymbol{\mathbf{C}} \boldsymbol\times ( \boldsymbol{\mathbf{A}} + \boldsymbol{\mathbf{B}} ) = - \boldsymbol{\mathbf{C}} \boldsymbol\times \boldsymbol{\mathbf{A}} - \boldsymbol{\mathbf{C}} \boldsymbol\times \boldsymbol{\mathbf{B}} = \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{C}} + \boldsymbol{\mathbf{B}} \boldsymbol\times \boldsymbol{\mathbf{C}} ~.
\end{equation}
从几何的角度理解,这个结论并不显然(见向量叉乘分配律的几何证明)。
3. 叉乘的坐标运算
坐标轴向量的叉乘
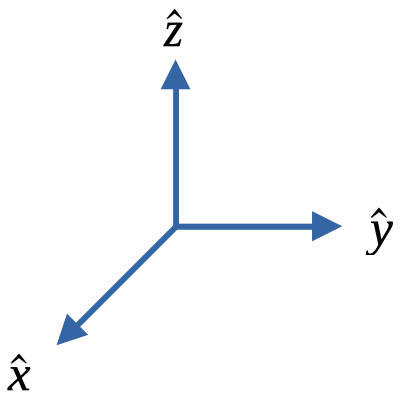
图 2:坐标轴
按照上面的定义,在右手系中,三个坐标轴的单位向量 $ \hat{\boldsymbol{\mathbf{x}}} , \hat{\boldsymbol{\mathbf{y}}} , \hat{\boldsymbol{\mathbf{z}}} $ 满足
\begin{equation}
\hat{\boldsymbol{\mathbf{x}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{y}}} = \hat{\boldsymbol{\mathbf{z}}}
\qquad
\hat{\boldsymbol{\mathbf{y}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{z}}} = \hat{\boldsymbol{\mathbf{x}}}
\qquad
\hat{\boldsymbol{\mathbf{z}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{x}}} = \hat{\boldsymbol{\mathbf{y}}} ~
\end{equation}
由
式 2 可得
\begin{equation}
\hat{\boldsymbol{\mathbf{y}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{x}}} = - \hat{\boldsymbol{\mathbf{z}}}
\qquad
\hat{\boldsymbol{\mathbf{z}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{y}}} = - \hat{\boldsymbol{\mathbf{x}}}
\qquad
\hat{\boldsymbol{\mathbf{x}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{z}}} = - \hat{\boldsymbol{\mathbf{y}}} ~
\end{equation}
根据定义,一个向量叉乘自身,模长为 $0$。所以叉乘结果是零向量 $ \boldsymbol{\mathbf{0}} $。于是又有
\begin{equation}
\hat{\boldsymbol{\mathbf{x}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{x}}} = \boldsymbol{\mathbf{0}}
\qquad
\hat{\boldsymbol{\mathbf{y}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{y}}} = \boldsymbol{\mathbf{0}}
\qquad
\hat{\boldsymbol{\mathbf{z}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{z}}} = \boldsymbol{\mathbf{0}} ~
\end{equation}
,
式 7 和
式 8 中共 9 条等式描述了 $ \hat{\boldsymbol{\mathbf{x}}} , \hat{\boldsymbol{\mathbf{y}}} , \hat{\boldsymbol{\mathbf{z}}} $ 中任意两个叉乘的结果。
任意向量的叉乘
把向量 $ \boldsymbol{\mathbf{A}} $ 和 $ \boldsymbol{\mathbf{B}} $ 分别在直角坐标系的三个单位向量展开,得到
\begin{equation}
\boldsymbol{\mathbf{A}} = a_x\, \hat{\boldsymbol{\mathbf{x}}} + a_y\, \hat{\boldsymbol{\mathbf{y}}} + a_z\, \hat{\boldsymbol{\mathbf{z}}} \qquad \boldsymbol{\mathbf{B}} = b_x\, \hat{\boldsymbol{\mathbf{x}}} + b_y\, \hat{\boldsymbol{\mathbf{y}}} + b_z\, \hat{\boldsymbol{\mathbf{z}}} ~
\end{equation}
$(a_x,a_y,a_z)$ 和 $(b_x,b_y,b_z)$ 分别是 $ \boldsymbol{\mathbf{A}} $ 和 $ \boldsymbol{\mathbf{B}} $ 的坐标。根据叉乘的分配律(
式 4 式 5 ),可得到如下 9 项
\begin{equation}
\begin{aligned}
\boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} ={} &(a_x\, \hat{\boldsymbol{\mathbf{x}}} + a_y\, \hat{\boldsymbol{\mathbf{y}}} + a_z\, \hat{\boldsymbol{\mathbf{z}}} ) \boldsymbol\times (b_x\, \hat{\boldsymbol{\mathbf{x}}} + b_y\, \hat{\boldsymbol{\mathbf{y}}} + b_z\, \hat{\boldsymbol{\mathbf{z}}} )\\
={} &+ a_x b_x( \hat{\boldsymbol{\mathbf{x}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{x}}} ) + a_x b_y( \hat{\boldsymbol{\mathbf{x}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{y}}} ) + a_x b_z( \hat{\boldsymbol{\mathbf{x}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{z}}} )\\
&+ a_y b_x( \hat{\boldsymbol{\mathbf{y}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{x}}} ) + a_y b_y( \hat{\boldsymbol{\mathbf{y}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{y}}} ) + a_y b_z( \hat{\boldsymbol{\mathbf{y}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{z}}} )\\
&+ a_z b_x( \hat{\boldsymbol{\mathbf{z}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{x}}} ) + a_z b_y( \hat{\boldsymbol{\mathbf{z}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{y}}} ) + a_z b_z( \hat{\boldsymbol{\mathbf{z}}} \boldsymbol\times \hat{\boldsymbol{\mathbf{z}}} )~.
\end{aligned} \end{equation}
注意每一项中的运算在
式 6 到
式 8 中都能找到答案,于是上式化为
\begin{equation}
\boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} = (a_y b_z - a_z b_y)\, \hat{\boldsymbol{\mathbf{x}}} + (a_z b_x - a_x b_z)\, \hat{\boldsymbol{\mathbf{y}}} + (a_x b_y - a_y b_x)\, \hat{\boldsymbol{\mathbf{z}}} ~.
\end{equation}
令 $ \boldsymbol{\mathbf{C}} = \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} $,则 $ \boldsymbol{\mathbf{C}} $ 的分量表达式为
\begin{equation}
\begin{cases}
c_x = a_y b_z - a_z b_y\\
c_y = a_z b_x - a_x b_z\\
c_z = a_x b_y - a_y b_x
\end{cases}~
\end{equation}
可以用
三阶行列式表示为
\begin{equation}
\boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} =
\begin{vmatrix}
\hat{\boldsymbol{\mathbf{x}}} & \hat{\boldsymbol{\mathbf{y}}} & \hat{\boldsymbol{\mathbf{z}}} \\
a_x & a_y & a_z\\
b_x & b_y & b_z
\end{vmatrix} ~\end{equation}
与普通行列式不同的是,这个行列式中第一行的元素是向量,所以得出的结果也是向量。
4. 等效的叉乘
图 3:$ \boldsymbol{\mathbf{A}} $ 与 $ \boldsymbol{\mathbf{B}} _i$ 相乘结果相同
根据定义 1 ,当两向量叉乘时,若把一个向量延着与另一个向量垂直的方向投影,叉乘结果不变。例如在图 3 中有
\begin{equation}
\boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} _1 = \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} _3 = \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} _2~.
\end{equation}
这是因为 $ \left\lvert \boldsymbol{\mathbf{B}} _i \right\rvert \sin\theta_i$ 就是投影后的 $ \boldsymbol{\mathbf{ \boldsymbol{\mathbf{B}} _2}} $ 的模长。另一种证明方法:所有指向虚线的 $ \boldsymbol{\mathbf{B}} _i$ 都可以表示为 $ \boldsymbol{\mathbf{B}} _2 + \lambda \boldsymbol{\mathbf{A}} $($\lambda$ 为任意实数)。根据分配律,有
\begin{equation}
\boldsymbol{\mathbf{A}} \boldsymbol\times ( \boldsymbol{\mathbf{B}} _2 + \lambda \boldsymbol{\mathbf{A}} ) = \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} _2 + \boldsymbol{\mathbf{A}} \boldsymbol\times (\lambda \boldsymbol{\mathbf{A}} ) = \boldsymbol{\mathbf{A}} \boldsymbol\times \boldsymbol{\mathbf{B}} _2~.
\end{equation}
5. 面积向量
在高中阶段面积只是一个标量概念,但在微积分和大学物理中,我们也可以把它拓展为向量。定义面积向量的模长是一个平面几何图形的面积,方向是其所在平面的两个法向量之一。具体到这里讨论的平行四边形,我们可以根据叉乘结果来明确定义平行四边形的面积向量。
例 1 求三角形或平行四边形的面积与法向量
空间直角坐标系中三角形的三点分别为 $O(0,0,0)$, $A(1,1,0)$, $B(-1,1,1)$。求三角形的面积和一个单位法向量。以这三点为顶点的平行四边形的面积显然是该三角形的两倍,所以下面只讨论三角形。
令 $O$ 到 $A$ 的向量和 $O$ 到 $B$ 的向量分别为
\begin{equation}
\begin{aligned}
\boldsymbol{\mathbf{a}} &= (1,1,0) - (0,0,0) = (1,1,0)\\
\boldsymbol{\mathbf{b}} &= (-1,1,1) - (0,0,0) = (-1,1,1)
\end{aligned} ~\end{equation}
三角形的面积为
\begin{equation}
S = \frac12 ab \sin \theta ~.
\end{equation}
其中 $\theta $ 是 $ \boldsymbol{\mathbf{a}} $ 与 $ \boldsymbol{\mathbf{b}} $ 的夹角。根据
式 1 ,有
1
\begin{equation}
S = \frac12 ab \sin \theta = \frac12 \left\lvert \boldsymbol{\mathbf{a}} \boldsymbol\times \boldsymbol{\mathbf{b}} \right\rvert ~.
\end{equation}
令
\begin{equation}
\boldsymbol{\mathbf{v}} = \boldsymbol{\mathbf{a}} \boldsymbol\times \boldsymbol{\mathbf{b}} =
\begin{vmatrix} \hat{\boldsymbol{\mathbf{x}}} & \hat{\boldsymbol{\mathbf{y}}} & \hat{\boldsymbol{\mathbf{z}}} \\ 1&1&0\\-1&1&1 \end{vmatrix}
= \hat{\boldsymbol{\mathbf{x}}} - \hat{\boldsymbol{\mathbf{y}}} + 2\, \hat{\boldsymbol{\mathbf{z}}} ~.
\end{equation}
坐标为 $(1,-1,2)$,模长为 $ \left\lvert \boldsymbol{\mathbf{v}} \right\rvert = \sqrt{1 + 1 + 2^2} = \sqrt 6$,所以面积为 $S = \sqrt 6 /2$。
根据叉乘的几何定义,$ \boldsymbol{\mathbf{v}} = (1,-1,2)$ 就是三角形的法向量,进行归一化
得单位法向量为
\begin{equation}
\hat{\boldsymbol{\mathbf{v}}} = \frac{ \boldsymbol{\mathbf{v}} }{ \left\lvert \boldsymbol{\mathbf{v}} \right\rvert } = \frac{(1,-1,2)}{\sqrt 6} = \left(\frac{\sqrt 6 }{6}, - \frac{\sqrt 6 }{6}, \frac{\sqrt 6 }{3} \right) ~.
\end{equation}
1. ^ 可见 $ \left\lvert \boldsymbol{\mathbf{a}} \boldsymbol\times \boldsymbol{\mathbf{b}} \right\rvert $ 是以 $ \boldsymbol{\mathbf{a}} $ 和 $ \boldsymbol{\mathbf{b}} $ 为边的平行四边形的面积。