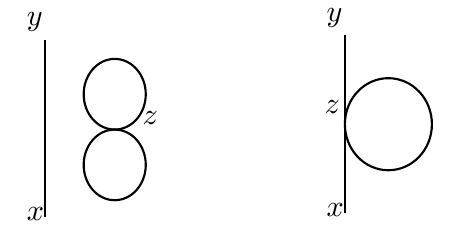贡献者: _Eden_
1. 导语
我们先以标量场 $\phi(x)$ 为例研究它的编时格林函数。
量子场论的重要研究对象就是散射过程的费曼矩阵元或 S 矩阵元,它给出了散射过程发生的概率,从而与实验中可直接观测到的散射截面、衰变率等物理量相联系。而根据相互作用场论的相关知识,LSZ 理论将 S 矩阵与编时格林函数联系了起来。为了求出相互作用场论的编时格林函数,我们又可以利用 Gell-Mann-Low 定理,将相互作用场论的真空态 $|\Omega\rangle$ 用自由场论的真空态 $|0\rangle$ 表示:
\begin{equation}
|\Omega\rangle = \lim\limits_{T_0\rightarrow \infty(1-i\epsilon)} \left(e^{-iE_0(t_0-(-T_0))}\langle \Omega|0\rangle \right) ^{-1}U(t_0,-T_0)|0\rangle~,
\end{equation}
从而可以得到以下公式
\begin{equation}
\left\langle \Omega \right\rvert T[\phi(x)\phi(y)] \left\lvert \Omega \right\rangle = \lim\limits_{T_0\rightarrow \infty(1-i\epsilon)}\frac{ \left\langle 0 \right\rvert T \left(\phi_I(x)\phi_I(y) \exp\left[-i\int_{-T_0}^{T_0} \,\mathrm{d}{t} H_I(t)\right] \right) \left\lvert 0 \right\rangle }{ \left\langle 0 \right\rvert T \left( \exp\left[-i\int_{-T_0}^{T_0} \,\mathrm{d}{t} H_I(t)\right] \right) \left\lvert 0 \right\rangle }~.
\end{equation}
其中 $H_I(t)$ 为相互作用表象下的相互作用哈密顿量。编时格林函数和 $\exp$ 指数可以理解为,首先将 $\exp$ 指数展开为幂级数,再对每一项进行编时操作。在微扰理论的框架下,$H_I$ 是微扰项,越高阶项的贡献越小。
于是最终问题变成了,如何求自由场论的编时格林函数。上式的形式仍然非常复杂,难以求解。幸运地是,我们有 Wick 定理,可以将编时格林函数的计算大大地简化,以至于可以用直观的费曼图来表示每一项的贡献。
2. Wick 定理
计算形如 $ \left\langle 0 \right\rvert T\phi_I(x_1)\cdots\phi_I(x_n) \left\lvert 0 \right\rangle $ 的关键是,将 $\phi_I(x_i)$ 分解为正频率和负频率两个部分 $\phi( x)=\phi^{(+)}( x)+\phi^{(-)}( x)$(以下省略下角标 $I$)。
\begin{equation}
\phi^{(+)}( x) = \int \frac{d{}^3{ \boldsymbol{\mathbf{p}} }}{(2\pi)^3} \frac{1}{\sqrt{2\omega_{ \boldsymbol{\mathbf{p}} }}}a_{ \boldsymbol{\mathbf{p}} } e^{-ipx} ,
\phi^{(-)}( x) = \int \frac{d{}^3{ \boldsymbol{\mathbf{p}} }}{(2\pi)^3} \frac{1}{\sqrt{2\omega_{ \boldsymbol{\mathbf{p}} }}}a_{ \boldsymbol{\mathbf{p}} }^\dagger e^{ipx} ~.
\end{equation}
那么由于产生湮灭算符的性质,正频率部分作用于 $ \left\lvert 0 \right\rangle $ 将得到 $0$。类似地,$\langle 0| \phi^{(-)}( x)=0$。将 $ \left\langle 0 \right\rvert \phi(x)\phi(y) \left\lvert 0 \right\rangle $ 中的场算符按正频率部分和负频率部分展开,可以得到
\begin{equation}
\begin{aligned}
\left\langle 0 \right\rvert \phi( x)\phi( y) \left\lvert 0 \right\rangle = \left\langle 0 \right\rvert \phi^{(+)}( x)\phi^{(-)}( y) \left\lvert 0 \right\rangle \\
= \left\langle 0 \right\rvert [\phi^{(+)}( x),\phi^{(-)}( y)] \left\lvert 0 \right\rangle ~.
\end{aligned}
\end{equation}
上式中的对易子看似是算符,实际上是 c 数。可以由下式看出。算上编时格林函数,我们有
\begin{equation}
\left\langle 0 \right\rvert T\phi( x)\phi( y) \left\lvert 0 \right\rangle =D_F(x-y)=\begin{cases}
\left\langle 0 \right\rvert [\phi^{(+)}( x),\phi^{(-)}( y)] \left\lvert 0 \right\rangle & (x^0>y^0)\\
\left\langle 0 \right\rvert [\phi^{(+)}( y),\phi^{(-)}( x)] \left\lvert 0 \right\rangle & (x^0< y^0)~.
\end{cases}
\end{equation}
上式中的 $D_F(x-y)$ 是费曼传播子
式 11 ,这里我们给它一个新的名称:两个场的 “缩并”。
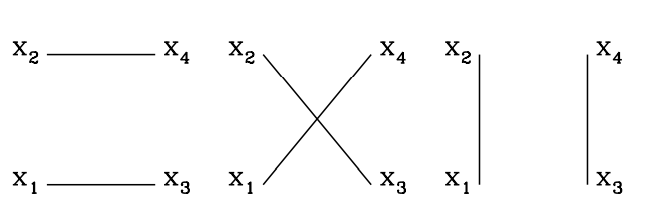
对于四个场算符构成的格林函数,$ \left\langle 0 \right\rvert T\phi(x_1)\phi(x_2)\phi(x_3)\phi(x_4) \left\lvert 0 \right\rangle $,用类似的推导,可以将每个场算符分解为正频率部分和负频率部分。那么最终结果就是,这四个场算符两两进行 “缩并” 的结果。所以
\begin{equation}
\begin{aligned}
\left\langle 0 \right\rvert T\phi(x_1)\phi(x_2)\phi(x_3)\phi(x_4) \left\lvert 0 \right\rangle =&D_F(x_1-x_2)D_F(x_3-x_4)+D_F(x_1-x_3)D_F(x_2-x_4)
\\&+D_F(x_1-x_4)D_F(x_2-x_3)~.
\end{aligned}
\end{equation}
这三项分别可以用下面的三张图表示
图 1:标量场路的四点编时格林函数的缩并图
用数学归纳法可以证明更多个场算符组成的编时格林函数的缩并结果。如果是奇数个场算符的编时格林函数,编时格林函数的值将为 $0$,因为缩并是成对的,总有一个场算符无法被缩并。而对于偶数个场算符组成的编时格林函数,则有许多种缩并方式,每种缩并方式都对结果有贡献,可以用缩并图来表示。
3. 相互作用顶点与费曼图
让我们来考虑两点编时格林函数 式 2 中分子的微扰展开,展开到相互作用项的第一阶:
\begin{equation}
\begin{aligned}
&\langle 0| T\left[\phi(x)\phi(y)+\phi(x)\phi(y)\left(-i\int_{-\infty}^{\infty} \,\mathrm{d}{t} H_I(t)\right)\right] | 0\rangle\\
&= \left\langle 0 \right\rvert T[\phi(x)\phi(y)] \left\lvert 0 \right\rangle
+\left(\frac{-i\lambda_0}{4!}\right) \int \,\mathrm{d}^{4}{z} \left\langle 0 \right\rvert T\left[ \phi(x)\phi(y)\phi^4(z) \right] \left\lvert 0 \right\rangle ~,
\end{aligned}
\end{equation}
其中第一项只存在 $\phi(x)$ 与 $\phi(y)$ 缩并的方式,因此对应于 $y$ 到 $x$ 一条线段的缩并图。现在考虑第二项,也就是一阶相互作用项。
注意到第二项的六点编时格林函数中 $z$ 出现了 $4$ 次,我们设置一个相互作用顶点 $z$。两点之间的连线代表两个时空坐标的场算符进行了一次缩并,这意味着缩并图中的顶点 $z$ 连出 $4$ 条连线。对于第二项,我们可以得到两种类型的缩并图,也被称为Feynman 图(费曼图)。拓扑同构的 Feynman 图给出的贡献是相同的,这是因为任意两点间的连线对应于传播子 $D_F(x-y)$,而相互作用顶点处对应与 $\lambda_0$ 相关的常数,所以我们上面得到的两种图实际上概括了所有两个外点、一个相互作用顶点的拓扑上互补等价的 Feynman 图。
图 2:$\phi^4$ 理论的两点编时格林函数的 $\lambda_0^1$ 阶的贡献
两张图分别对应两种不同的缩并方式,并且我们需要分别计算它们的缩并方案数。具体的计算可以得到
\begin{equation}
\begin{aligned}
&\quad \left\langle 0 \right\rvert T[\phi(x)\phi(y)] \left\lvert 0 \right\rangle
+\left(\frac{-i\lambda_0}{4!}\right) \int \,\mathrm{d}^{4}{z} \left\langle 0 \right\rvert T[\phi(x)\phi(y)\phi^4(z) ] \left\lvert 0 \right\rangle \\
&=D_F(x-y)+3\cdot \left(\frac{-i\lambda_0}{4!}\right)\int \,\mathrm{d}^{4}{z}
\left\langle 0 \right\rvert \overset{1}{\phi}_x\overset{1}{\phi}_y \overset{2}{\phi}_z\overset{2}{\phi}_z\overset{3}{\phi}_z \overset{3}{\phi}_z \left\lvert 0 \right\rangle \\
&\quad +4\cdot 3 \cdot \left(\frac{-i\lambda_0}{4!}\right)\int \,\mathrm{d}^{4}{z}
\left\langle 0 \right\rvert \overset{1}{\phi}_x\overset{2}{\phi}_y \overset{1}{\phi}_z\overset{2}{\phi}_z\overset{3}{\phi}_z \overset{3}{\phi}_z \left\lvert 0 \right\rangle \\
&=D_F(x-y)+\frac{1}{8} (-i\lambda_0)\int \,\mathrm{d}^{4}{z} D_F(x-y)D_F(z-z)D_F(z-z) \\
&\quad + \frac{1}{2} (-i\lambda_0)\int \,\mathrm{d}^{4}{z} D_F(x-z)D_F(y-z)D_F(z-z)~.
\end{aligned}
\end{equation}
上面我们只计算了相互作用的一阶,对于二阶、三阶以至于 $n$ 阶,可以想象到 Feynman 图中将出现 $n$ 个内点,这些内点是由于相互作用而引入的点,连出 $4$ 条连线,也被称为相互作用顶点。Feynman 图中除了相互作用顶点以外,还有外点对应着我们原本希望计算的编时格林函数中出现的点,正如上面的两点编时格林函数,反映到 Feynman 图中则是两个外点 $x$ 与 $y$,它们只连出一条边,这条边被称为外线。如果一个 Feynman 图在拓扑上是连通的,那么它被称为连通图,否则被称为非连通图;与任何外点都不连通的部分被称为真空图。
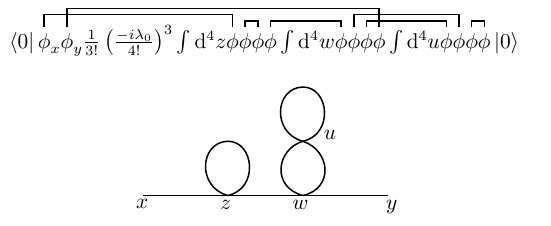
当相互作用继续展开到高阶项,则要计算所有可能的 Feynman 图的贡献。例如相互作用的第三阶,对应的 Feynman 图有很多,有 $3$ 个内点,$6$ 条边,其中 $2$ 条边是外线。下式代表了其中一种缩并方式:
图 3:$\phi^4$ 理论两点编时格林函数的 $\lambda_0^3$ 阶的其中一个 Feynman 图
我们试图计算这个 Feynman 图的贡献。图中每条边对应一个传播子,每个顶点可以对应一个常数 $(-i\lambda_0)$。除此以外还有一个系数 $1/(3!\cdot (4!)^3)$,源自 $\exp$ 指数展开后的因子 $1/3!$ 以及相互作用项本来就拥有的 $1/4!$ 因子。除此以外我们需要计算这个 Feynman 图对应的缩并方案数。$z,w,u$ 三个时空点处于不等价的地位,因此可以对它们作任意的置换,对应方案数乘 $3!$;$z$ 点的四个场算符要依次取出两个分别与 $x$ 和 $w$ 缩并,对应方案数乘 $4\cdot 3$;类似地,$w$ 点要依次取出四个,对应方案数乘 $4\cdot 3\cdot 2\cdot 1$;$u$ 点的四个场算符要依次取出两个,对应方案数乘 $4\cdot 3$;最后,注意 $w$ 与 $u$ 之间的两条边拥有等价的地位,所以前面的计数过程中实际上有重复,要乘以 $1/2!$ 消去重复。最终我们计算出这个 Feynman 图的系数为
\begin{equation}
\frac{1}{S}=\frac{1}{3!\cdot (4!)^3}\cdot 3! \cdot (4\cdot 3)\cdot (4\cdot 3\cdot 2\cdot 1)\cdot (4\cdot 3)\cdot \frac{1}{2!}=\frac{1}{2!\cdot 2!\cdot 2!}~.
\end{equation}
因此对称因子 $S=8=2!\cdot 2!\cdot 2!$。它的可以被解释为:$z$ 点处的一个自环(传播子首尾连在这个顶点上),首尾交换不变,贡献对称因子 $2$;$u$ 处也有一个自环,首尾交换不变,贡献对称因子 $2$;$u,w$ 间的两条边是全同的,交换它们不变,贡献对称因子 $2$。注意到,原本 $S$ 中还会出现因子 $3!$,但正因为 $z,w,u$ 三个顶点是处于不等价的地位的,所以在上面的计算中才会消去这个因子,换言之,如果 $z,w,u$ 三者等价,即交换这些顶点的位置仍可以使 Feynman 图同构于原来的图,那么将贡献对称因子 $3!$。可以将这样的规则推广到更复杂的 Feynman 图的情况,对称因子的计算规则可以具体地总结为:
定理 1 对称因子的计算规则
- 如果一个传播子首尾连接于一个顶点,那么贡献对称因子 $2$。
- 如果两个点之间连接着 $n$ 个全同传播子,那么贡献对称因子 $n!$。
- 如果 Feynman 图中有一个 $n$ 阶旋转对称轴,即存在一个 $n$ 阶的置换对称不变性,那么它贡献对称因子 $n!$。
现在我们可以总结出 Feynman 图贡献的计算方法:
定理 2 $\phi^4$ 理论的 Feynman 规则(实空间)
- 对每一个从 $x$ 到 $y$ 的传播子,写下 $D_F(x-y)$。
- 对每一个相互作用顶点 $z$,写下 $(-i\lambda_0)\int \,\mathrm{d}^{4}{z} $。
- 除以该图对称因子 $S$。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。