贡献者: zhousiyi
前面一节我们讲到如何对标量场进行量子化。这一节我们来看看如何写出标量场理论的谱。
现在我们来定义真空态。
定义 1 真空态 $|0\rangle$
对于所有的 $\mathbf p$,都有 $a_{\mathbf p}|0\rangle=0$.如果我们不考虑真空能的话。这个态的能量为 $E=0$。
所有其它的态都可以通过在真空态 $|0\rangle$ 前面加上产生算符来构建。一般来说,态 $a^\dagger_{\mathbf p}a^\dagger_{\mathbf q}|0\rangle$ 哈密顿量 $H$ 的能量为 $\omega_{\mathbf\cdots p}+\omega_{\mathbf q}+\cdots$ 的本征态。
由经典场论基础文章中的式 44 我们可以写出总动量算符
\begin{equation}
\mathbf P = -\int d^3 x \Pi(\mathbf x) \nabla \phi ~.
\end{equation}
算符 $a_{\mathbf p}\dagger\dagger$ 能够产生动量为 $\mathbf \omega$,能量为 $\omega_{\mathbf p} = \sqrt{|\mathbf p|^2+m^2}$ 的态。我们把这些激发态叫做粒子。
现在我们来看粒子的统计性质。我们来考虑一个二粒子态 $a^\dagger_{\mathbf p}a^\dagger_{\mathbf q}| 0 \rangle$。因为 $a^\dagger_{\mathbf p}$ 和 $a^\dagger_{\mathbf q}$ 是对易,这个态和 $a^\dagger_{\mathbf q}a^\dagger_{\mathbf p}| 0 \rangle$ 是等价的。一个模式 $\mathbf p$ 可以激发出任意多的粒子数。由此我们得出结论:克莱因-戈登粒子遵守玻色-爱因斯坦统计。
现在我们来定归一化条件 $\langle 0 | 0 \rangle = 1$。单粒子态 $|\mathbf p\rangle\propto a^\dagger_{\mathbf p} | 0 \rangle$ 的归一化条件 $\langle \mathbf p| \mathbf q\rangle = (2\pi)^3\delta^{(3)}(\mathbf p - \mathbf q)$ 不是洛仑兹不变的。因为如果我们考虑洛仑兹 boost
\begin{equation}
p'_3 = \gamma ( p_3+\beta E)~,\quad E' = \gamma(E+\beta p_3)~.
\end{equation}
考虑 $\delta$ 函数恒等式
\begin{equation}
\delta (f(x) - f(x_0)) = \frac{1}{|f'(x_0)|}\delta(x-x_0)~.
\end{equation}
我们可以计算 $\delta$ 函数在
式 2 这样的洛仑兹变换下是怎样变化的。变化如下
\begin{equation}
\begin{aligned}
\delta ^{(3)}(\mathbf p -\mathbf q)\delta& = \delta^{(3)}(\mathbf p' - \mathbf q') \cdot \frac{dp'_3}{dp_3}\\
& = \delta^{(3)}(\mathbf p' - \mathbf\gamma q') \gamma\beta\bigg( 1+\beta \frac{dE}{dp_3} \bigg) \\
& = \delta^{(3)}(\mathbf p' - \mathbf q') \frac{\gamma }{E} (E+ \beta p_3) \\
& = \delta^{(3)} (\mathbf p'-\mathbf q') \frac{E'}{E}~.
\end{aligned}
\end{equation}
从这个计算我们可以看出 $E_{\mathbf p}\delta^{(3)}(\mathbf p - \mathbf q)$ 是洛仑兹不变的。因此我们定义
\begin{equation}
|\mathbf p \rangle = \sqrt{2 E_{\mathbf p}} a^\dagger_{\mathbf p} | 0 \rangle~.
\end{equation}
归一化条件为
\begin{equation}
\langle \mathbf p | \mathbf q \rangle = 2 E_{\mathbf p} (2\pi)^3 \delta^{(3)} (\mathbf p - \mathbf q)~.
\end{equation}
洛仑兹变换 $\Lambda$ 可以用幺正算符 $U(\Lambda)$ 来实现。由归一化条件可以推出
\begin{equation}
U(\Lambda)|\mathbf p\rangle = |\Lambda \mathbf p \rangle ~.
\end{equation}
这个变换可以作用在算符 $a^\dagger_{\mathbf p}$ 上面,我们可以写为
\begin{equation}
U(\Lambda)a^\dagger_{\mathbf p}U^{-1}(\Lambda) = \sqrt{\frac{E_{\Lambda \mathbf p}}{E_{\mathbf p}}} a^\dagger_{\mathbf p}~.
\end{equation}
单粒子态的完备性规则为
\begin{equation}
(\boldsymbol 1)_{\rm 1-particle} = \int \frac{d^3p}{(2\pi)^3} |\mathbf p\rangle \frac{1}{2 E_{\mathbf p}} \langle \mathbf p |~,
\end{equation}
像这样的积分以后会经常出现。积分
\begin{equation}
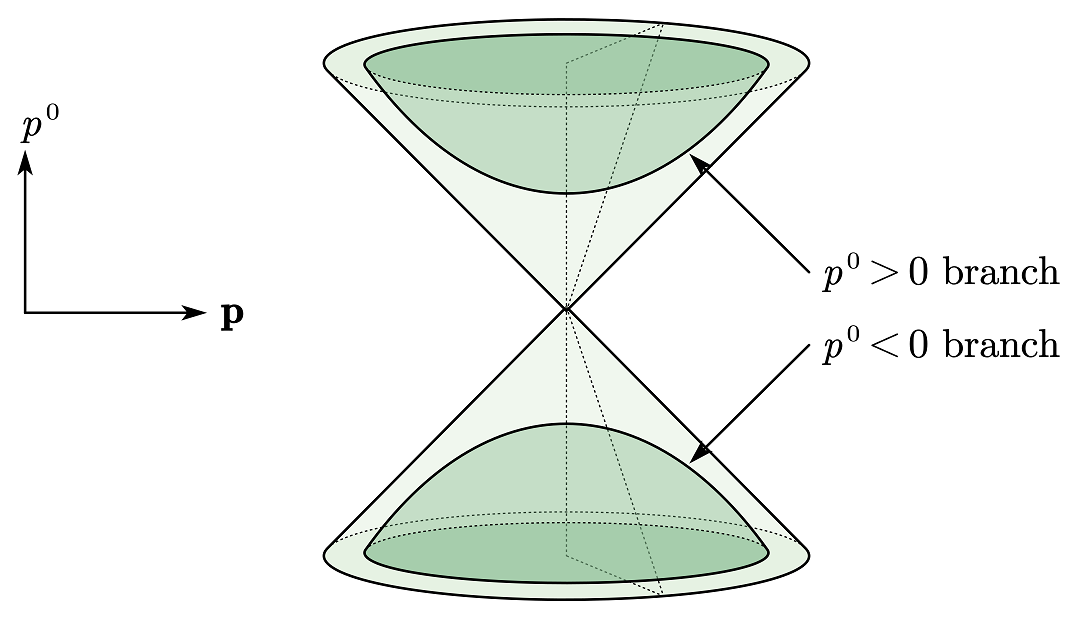
\int \frac{d^3p}{(2\pi)^3} \frac{1}{2 E_{\mathbf p}} = \int \frac{d^4 p}{(2\pi)^4} (2\pi) \delta(p^2 - m^2) \bigg|_{p^0>0}~
\end{equation}
是一个洛仑兹不变的三动量积分。这是因为如果 $f(p)$ 是一个洛仑兹不变的函数的话,$\int d^3 p f(p)/(2E_{\mathbf p})$ 也将是一个洛仑兹不变的函数。
图 1:洛仑兹不变的三动量积分是在上面的双曲面进行的。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。