节流过程

贡献者： _Eden_

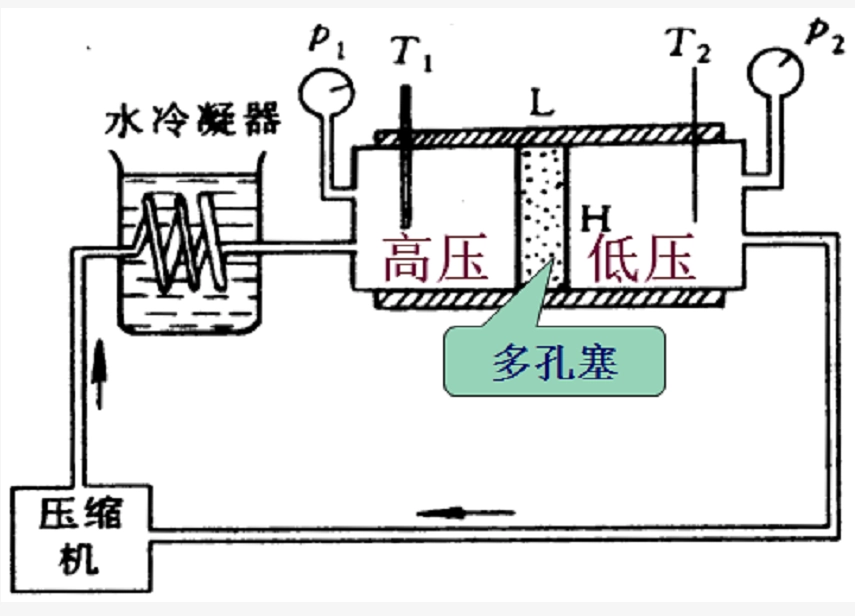
　　 绝热条件下，气体从高压的一边经过多孔塞不断地流到低压的一边，并达到定常状态；多孔塞两边各维持着较高的气压 $P_1$ 和较低的气压 $P_2$，这个过程叫做节流过程。

　　 由于整个过程是绝热的，所以 $\Delta Q=\Delta U+P\Delta V=0$。设气体在通过多孔塞前内能为 $U_1$,体积为 $V_1$，通过多孔塞后内能为 $U_2$，体积为 $V_2$，那么 $U_2-U_1+P_2V_2-P_1V_1=0$，即 $U_2+P_2V_2=U_1+P_1V_1$。我们可以定义系统的另一状态函数：焓 $H=U+PV$。那么 $H_1=H_2$，在节流过程前后气体的焓值相等。

　　 现在我们要研究在节流过程中，气体降温 $\Delta T$ 与压强的变化 $\Delta P$ 的关系。由于是等焓过程，我们可以定义焓不变的条件下气体温度随压强的变化率，称为焦汤系数：

　　 将状态函数 $H$ 看成 $T,P$ 的函数 $H(T,P)$，那么

　　 最后一个等号可以由焓的方程式 19 推出。对理想气体来说，等压膨胀系数 $\alpha=\frac{1}{T}$，焦汤系数为　$0$，气体没有降温。这个结果并不出人意料，因为理想气体的分子间没有互相作用力，内能只是温度的函数，而且 $p_1V_1=p_2V_2$，等焓过程就是等内能过程，也是等温过程。

　　 但对于一般气体，例如范德瓦尔斯气体，若 $\alpha T>1$，有 $\mu>0$，当气体从高压区经过多孔塞到低压区就会降温。从能量转换的角度看，气体在膨胀的过程中分子相互作用势增加，一部分分子动能转换为相互作用势，所以气体温度降低。