连通性

贡献者： JierPeter; addis

1. 连通性的概念

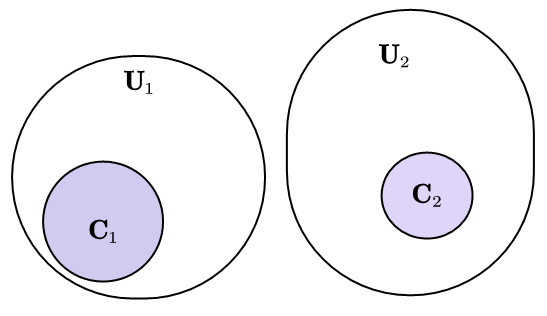
　　 什么叫连通性？直观来说，在平面 $\mathbb{R}^2$ 上画两个不相交也不相切的圆，那么这两个圆所包含的区域就是不连通的。不连通的各部分显然是可以被 “孤立” 出来的，也就是说，如果两圆不相交也不相切，就一定能各自找到一个开集，让这两个圆分别被一个开集包含，而这两个开集还互不相交。这就是定义连通性的方法。

　　 我们把这两个圆包含的区域单独拿出来，构造一个子空间。在这个子空间中，两个圆各自有一个特点：它们既是开集也是闭集。如果将两个圆分别记为 $C_1$ 和 $C_2$，子空间记为 $A=C_1\cup C_2$，包含它们的开集分别是 $U_1\supseteq C_1$ 和 $U_2\supseteq C_2$，且 $U_1\cap U_2=\varnothing$，那么由子拓扑的定义，$C_1=C_1\cap U_1$ 是子空间的开集，同理 $C_2$ 也是子空间的开集；然而在子空间中还有 $C_1=A-C_2$，所以 $C_1$ 还应该是一个闭集，同理 $C_2$ 也是一个闭集。

　　 如果你选择的是一个连通的空间，比如说一个圆所包含的区域构造的子空间，那么这种 “既开又闭” 的情况是不会存在的。因此，我们可以根据既开又闭的性质来定义连通性。

　　 注意，定义孤立分支的时候特别强调了 $A$ 是一个非空真子集，这样就把 $\varnothing$ 和 $X$ 本身排除在外了，因为按照定义，它们俩必须是既开又闭的。在上图中的 $C_1$ 和 $C_2$ 就是两个孤立分支。

　　 有了孤立分支的概念，就能直接引入连通性的概念了：

　　 显然，$X$ 的一个孤立分支本身就是连通的，而任何严格大于孤立分支的子集则不连通。因此，我们也把孤立分支称为连通分支或者连通单元。

　　 连通性也可以用别的方式定义。

　　 对于任何拓扑空间，我们可以讨论这个空间本身是不是连通的，也可以研究各个子集构成的子空间是不是连通的。如果一个子集作为拓扑空间是连通的，我们就说这是一个连通子集（connected subset）。

2. 连通性的性质

　　 引入连通性的概念，一个关键的好处是它刻画了拓扑空间的一个基本性质。正如我们在同胚中提过的，连通性是一个同胚不变性，也就是说，同胚的拓扑空间的连通性是完全一致的。这由以下定理保证：

　　 应用 “开集的逆映射还是开集” 可以很容易地证明这一定理。考虑到同胚映射在两个方向（$X\rightarrow Y$ 和 $Y\rightarrow X$）上都是连续映射，那么同胚映射把两个拓扑空间的连通子集彼此对应起来了。

　　 在例 1 中我们知道 $S$ 和 $\bar{S}$ 都是连通的，这不是偶然的。

　　 由 “集合的内部、外部和边界” 中推论 1 可知，定理 2 中定义的 $B$ 就是 $A$ 添上若干边界点生成的；如果把边界点全都添上了，那就是 $\bar{A}$。