SciPy 数值微分与积分
贡献者: shizy0808; addis; Li Hao-Hao
SciPy 函数库在 NumPy 库的基础上增加了众多的数学、科学以及工程计算中常用的库函数。例如线性代数、常微分方程数值求解、信号处理、图像处理、稀疏矩阵等等。
使用 SciPy 库之前需要先导入库,
import scipy#导入scipy中所有模块
from scipy import integrate#导入其中积分模块
1. 数值积分
数值积分是对定积分的数值求解。例如可以利用数值积分计算某个形状的面积。下面让我们来考虑一下如何计算半径为 1 的半圆的面积,根据圆的面积公式,其面积应该等于 $\pi$。单位半圆曲线可以用函数 half_circle() 表示,对应计算积分的代码如下:
def half_circle(x):
return (1-x**2)**0.5
from scipy import integrate
res, err = integrate.quad(half_circle, -1, 1)
print(res,err)
输出:
1.5707963267948983 1.0002354500215915e-09
quad 函数,这里不仅返回了积分结果,还给出来计算误差。多重定积分的求值可以通过多次调用 quad 函数实现,为了调用方便,integrate 库提供了 dblquad 函数
进行二重定积分,tplquad 函数进行三重定积分。
dblquad 函数的调用方式为:
dblquad(func2d, a, b, gfun, hfun, args=())
func2d(y,x) 函数进行二重积分,其中 a,b 为变量 $x$ 的积分区间,$ a < b $,而 gfun(x) 到 hfun(x) 为变量 $y$ 的积分区间,注意被积函数中变量 $ y $ 与 $ x $ 的位置必须和相应的积分限位置对应。args=() 为向函数 func2d(y,x) 中传递的参量,比如函数 func2d(y,x,c,d,f),其中 c,d,f 为向被积函数传递的参量,而 y,x 为积分变量,这一项是可选择的,若没有需要传递的参量可以不加该项。
tblquad 函数的调用方式与上面一样。
2. 数值解微分方程组
scipy.integrate 库提供了数值积分和常微分方程组求解算法 odeint。
odeint() 函数需要至少三个变量,第一个是微分方程函数,第二个是微分方程初值,第三个是微分的自变量。
下面让我们来看看如何用 odeint 计算十分经典的洛仑兹吸引子的轨迹。洛仑兹吸引子由下面的三个微分方程定义:
\begin{align}
&\dot{x}=\sigma~.\\
&\dot{y}=x(\rho-y)~.\\
&\dot{z}=xy-\beta~.
\end{align}
from scipy.integrate import odeint
import numpy as np
def lorenz(w, t, p, r, b):
# 给出位置矢量w,和三个参数p, r, b计算出
# dx/dt, dy/dt, dz/dt的值
x, y, z = w
# 直接与lorenz的计算公式对应
return np.array([p*(y-x), x*(r-z)-y, x*y-b*z])
t = np.arange(0, 30, 0.01) # 创建时间点
# 调用ode对lorenz进行求解, 用两个不同的初始值
track1 = odeint(lorenz, (0.0, 1.00, 0.0), t, args=(10.0, 28.0, 3.0))
track2 = odeint(lorenz, (0.0, 1.01, 0.0), t, args=(10.0, 28.0, 3.0))
from mpl_toolkits.mplot3d import Axes3D
import matplotlib.pyplot as plt
fig = plt.figure()
ax = Axes3D(fig)
ax.plot(track1[:,0], track1[:,1], track1[:,2])
ax.plot(track2[:,0], track2[:,1], track2[:,2])
plt.show()
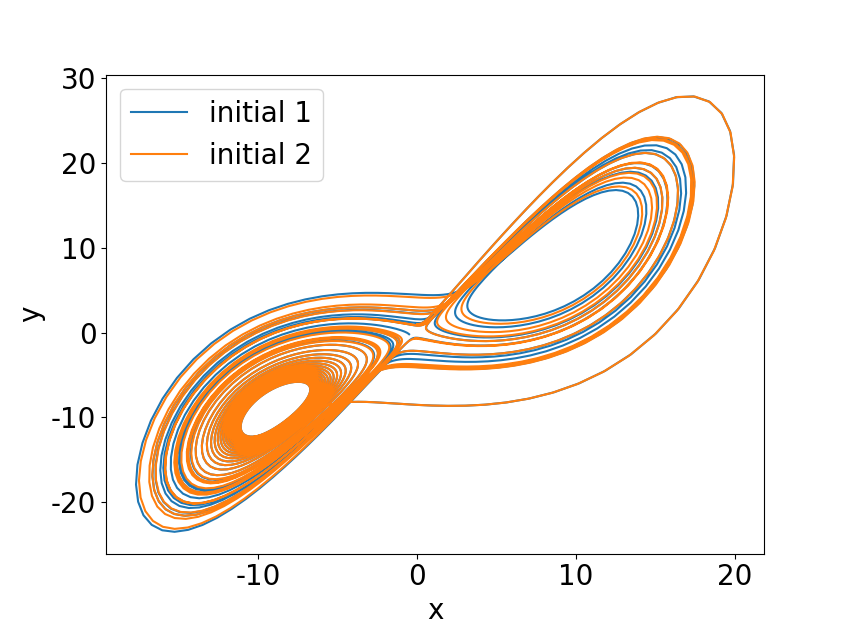
图 1:洛伦兹微分方程数值解
这里我们还使用到了第四个参数 args,它是一个 tuple 类型,给函数传递额外的参数。我们看到即使初始值只相差 0.01,两条运动轨迹也是完全不同的。
在程序中先定义一个 lorenz 函数,它的任务是计算出某个位置的各个方向的微分值,这个计算直接根据洛仑兹吸引子的公式得出。然后调用 odeint,对微分方程求解,odeint 有许多参数,这里用到的四个参数分别为:
-
lorenz,它是计算某个位移上的各个方向的速度(位移的微分) -
(0.0, 1.0, 0.0),位移初始值。计算常微分方程所需的各个变量的初始值 -
t,表示时间的数组,odeint对于此数组中的每个时间点进行求解,得出所有时间点的位置 -
args,这些参数直接传递给lorenz函数,因此它们都是常量
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。
友情链接: 超理论坛 | ©小时科技 保留一切权利