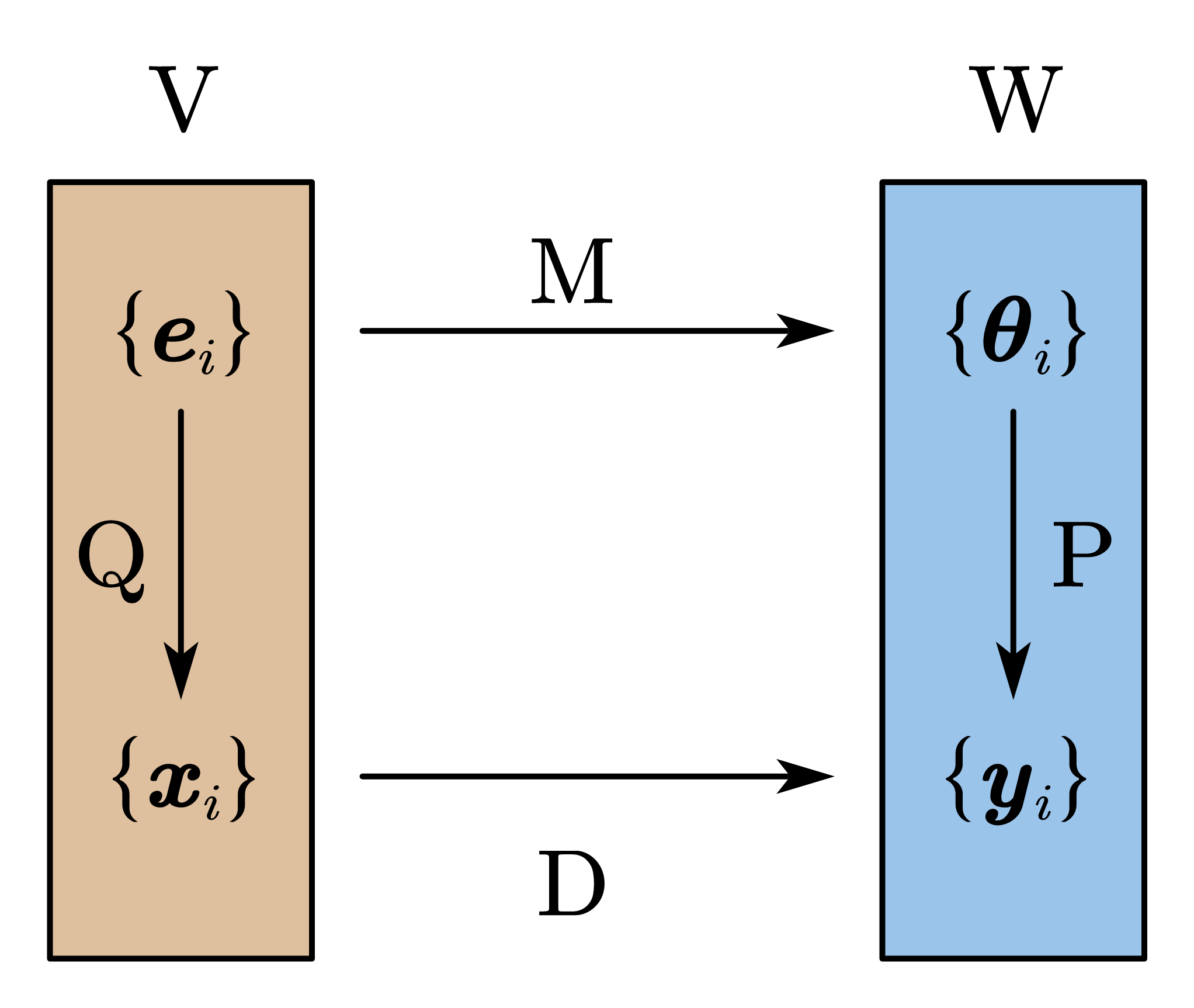奇异值分解（SVD）

贡献者： 叶月2_; addis

　　 本节默认在复数域及酉空间下讨论。

1. 定理陈述

2. 证明过程

　　 我们先从可逆方阵证起，然后再过渡到不要求可逆的任意复矩阵。

　　 证明：因为 $ \boldsymbol{\mathbf{M}} ^\dagger \boldsymbol{\mathbf{M}} $ 是半正定厄米矩阵，必存在一组标准正交基使之对角化，设为 $ \boldsymbol{\mathbf{A}} $，对应的过渡矩阵为酉方阵 $ \boldsymbol{\mathbf{Q}} $，则该过程表示为 $ \boldsymbol{\mathbf{Q}} \boldsymbol{\mathbf{M}} ^\dagger \boldsymbol{\mathbf{MQ}} ^\dagger = \boldsymbol{\mathbf{A}} $。左右取行列式可证 $ \boldsymbol{\mathbf{A}} $ 是可逆矩阵。在这组基下，对对角元计算后，我们可以得到 $ \boldsymbol{\mathbf{A}} ^{\frac{1}{2}}, \boldsymbol{\mathbf{A}} ^{-\frac{1}{2}}$，显然互逆。

　　 我们可以把 $ \boldsymbol{\mathbf{M}} $ 表示为 $ \boldsymbol{\mathbf{MQ}} ^\dagger \boldsymbol{\mathbf{A}} ^{-\frac{1}{2}} \boldsymbol{\mathbf{A}} ^{\frac{1}{2}}Q$，和式 2 比较，我们需要验证 $ \boldsymbol{\mathbf{MQ}} ^\dagger \boldsymbol{\mathbf{A}} ^{-\frac{1}{2}}$ 是酉方阵。

　　 设 $ \boldsymbol{\mathbf{P}} ^\dagger = \boldsymbol{\mathbf{M}} \boldsymbol{\mathbf{Q}} ^\dagger \boldsymbol{\mathbf{A}} ^{-\frac{1}{2}}$，则 $ \boldsymbol{\mathbf{P}} = \boldsymbol{\mathbf{A}} ^{-\frac{1}{2}} \boldsymbol{\mathbf{Q}} \boldsymbol{\mathbf{M}} ^\dagger $，则

　　 在定理 2 的陈述里 $ \boldsymbol{\mathbf{D}} $ 也是可逆矩阵，这并非偶然。考虑到 $ \boldsymbol{\mathbf{P}} ^{-1}= \boldsymbol{\mathbf{P}} ^\dagger $，该定理实际上是 $ \boldsymbol{\mathbf{M}} $ 的广义相似变换。如下图所示，线性映射 $f:V\rightarrow W$ 在不同基下有不同表示。设 $\{ \boldsymbol{\mathbf{e}} _i\},\{ \boldsymbol{\mathbf{\theta}} _i\}$ 是 $V,W$ 的旧基，且 $f$ 在该基下的表示为 $ \boldsymbol{\mathbf{M}} $。$ \boldsymbol{\mathbf{P}} , \boldsymbol{\mathbf{Q}} $ 是对应 $W,V$ 的从旧基到新基的过渡矩阵，则 $ \boldsymbol{\mathbf{D}} $ 就自然是 $f$ 在新基下的表示了。作为 $f$ 的不同表示，$ \boldsymbol{\mathbf{M}} $ 与 $ \boldsymbol{\mathbf{N}} $ 的行列数相同，秩也相同。

　　 如此一来，我们似乎可以拓展该定理至 $ \boldsymbol{\mathbf{M}} $ 不可逆的情况。

　　 换一个方式表述，引理 1 实际上是在说对于酉空间的任意线性映射 $f$，原像和像空间存在一组标准正交基，使得 $f$ 在该基下是式 4 所示的块对角形式。

　　 考虑到 $ \operatorname {dim}V= \operatorname {dim} \operatorname {ker}f+ \operatorname {dim} \operatorname {Im}f$，我们可以在 $ \operatorname {ker}f$ 内选一组标准正交基，然后扩展到全空间。设 $k= \operatorname {dim} \operatorname {ker}f,s= \operatorname {dim} \operatorname {Im}f$。则在该组基下，$f$ 的后 $k$ 列必为 $0$。

　　 同理，$ \operatorname {Im}f$ 作为 $W$ 的子空间，也可以找到一组标准正交基，并拓展到其正交补。因而除去前 $s$ 行，其他行都为 $0$。如此我们就证明了 $f$ 具有式 4 所示的块对角形式，其中 $ \boldsymbol{\mathbf{N}} $ 必为满秩的 $s\times s$方阵，即其可逆。如若不然，$ \operatorname {Im}f\cap \operatorname {ker}f\neq\{ \boldsymbol{\mathbf{0}} \}$。

　　 现在我们来证明奇异值分解定理。 对于任意复矩阵$ \boldsymbol{\mathbf{M}} $，我们可以分解为引理 1 的形式。那么对于满秩$ \boldsymbol{\mathbf{N}} $ 矩阵，自然而然的，我们可以利用定理 2 进行进一步的分解。设该分解表示为 $ \boldsymbol{\mathbf{N}} = \boldsymbol{\mathbf{T}} ^\dagger \boldsymbol{\mathbf{D}} ' \boldsymbol{\mathbf{F}} $，其中 $ \boldsymbol{\mathbf{D}} '$ 为可逆对角矩阵。

　　 构造复矩阵 $ \boldsymbol{\mathbf{T}} _1, \boldsymbol{\mathbf{S}} _1$，其中 $ \boldsymbol{\mathbf{E}} _1, \boldsymbol{\mathbf{E}} _2$ 是用作填充的单位矩阵，比如 $ \boldsymbol{\mathbf{E}} _1$ 使得 $ \boldsymbol{\mathbf{T}} _1$ 的行数等于 $ \boldsymbol{\mathbf{S}} ^\dagger $ 的列数。

　　 易证 $ \boldsymbol{\mathbf{T}} _1 ^\dagger , \boldsymbol{\mathbf{F}} _1$ 是酉矩阵，可见 $ \boldsymbol{\mathbf{D}} $ 便是定理里要求的对角矩阵，$ \boldsymbol{\mathbf{P}} ^\dagger = \boldsymbol{\mathbf{S}} ^\dagger \boldsymbol{\mathbf{T}} _1 ^\dagger , \boldsymbol{\mathbf{Q}} = \boldsymbol{\mathbf{F}} _1 \boldsymbol{\mathbf{Q}} '$。