贡献者: _Eden_; addis
11879 年霍尔(E. C. Hall)首先观察到,把一载流导体薄片放在磁场中时,如果磁场方向垂直于薄片平面,则在薄片的上、下两侧面会出现微弱的电势差。这一现象称为霍尔效应(Hall effect)。此电势差称为霍尔电势差。实验测定,霍尔电势差的大小与电流 $I$ 及磁感应强度 $B$ 成正比,而与薄片沿 $\mathbf B$ 方向的厚度 $d$ 成反比。它们的关系可写成:
\begin{equation}
V = R_{\mathrm{H}} \frac{I B}{d}~.
\end{equation}
其中 $R_H$ 是
霍尔系数(Hall coefficient),等于
自由电子电荷量的体密度 $ne$ 的倒数(式 4 ),单个电子的带电量为 $-e$。
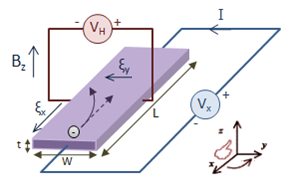
图 1:霍尔效应示意图(来自维基百科)
1. 半导体中的霍尔效应
1879 年霍耳在研究带电导体在磁场中电学性质时发现了这一效应,后来发现半导体中的霍耳效应比金属大几个数量级。
在载流导体材料中,自由电子为 “载流子”2,那么自由电子定向移动在磁场中漂移产生霍尔电压。在一些半导体元件中,载流子还可以是空穴,此时半导体被称为 P 型半导体;与自由电子不同,空穴的带电量为 $+e$,同样可以在电场作用下定向运动,在磁场中漂移产生霍尔电压。以自由电子为载流子的半导体被称为 N 型半导体。
霍尔系数反比于载流子密度,而导体中自由电子的密度比半导体中载流子的密度要大得多,这意味着导体的霍尔效应很不显著,人们一般用半导体作为霍尔元件。
2. 霍尔电阻的推导
平衡时电场力与洛伦兹力相等
\begin{equation}
Ee = vBe~,
\end{equation}
令 $J$ 为电流密度 $J=nev$
\begin{equation}
E = JB/(ne)~.
\end{equation}
两端电压为
\begin{equation}
V = IB/(d n e)~,
\end{equation}
\begin{equation}
R = V/I = B/(d n e)~.
\end{equation}
于是定义 $R_H=1/(nq)$,我们最终得到了
\begin{equation}
V=R_H\frac{IB}{d}~.
\end{equation}
或者可以对式 5 换一种表达。考虑电阻率 $\rho$3,由于霍尔电阻只和材料的厚度 $d$ 有关,和另两条边的长度 $w,L$ 无关,所以可以定义电阻率 $\rho$ 为 $R\equiv\rho /d$,
\begin{equation}
\rho\equiv Rd=\frac{B}{ne}~.
\end{equation}
那么代入 $R=V/I$ 可以得到
\begin{equation}
\begin{aligned}
&\frac{\rho }{d} =R= \frac{V}{I}\Rightarrow \frac{\rho I}{dw}=\frac{V}{w}~,\\
&\rho \cdot J = E,\quad J= \frac{I}{dw}=\frac{I}{S},\quad E=\frac{V}{w}
\end{aligned}
\end{equation}
因此我们利用电阻率、电流密度、电场强度得到了一个更简单的表达式
\begin{equation}
\rho\cdot J=E~.
\end{equation}
假设电流 $I$ 是沿 $y$ 方向,产生的霍尔电压是沿 $x$ 方向,那么
\begin{equation}
E_x = \rho_{xy} J_y~.
\end{equation}
事实上如果加 $x$ 方向的电流,会产生 $-y$ 方向的霍尔电压,这是因为材料旋转 90 度以后的物理规律一般是不变的。$E_y=-\rho_{xy} J_x\equiv \rho_{yx}J_x$。
$\rho_{xy}=-\rho_{yx}$ 被称为横向的霍尔电阻率。
3. Drude 模型与经典霍尔效应
下面我们从 Drude 模型的视角看待经典霍尔效应,并推导出它当对二维材料加 $z$ 方向的磁场时材料的电导率 $\sigma$ 与电阻率张量 $\rho$ 的理论计算结果。$\sigma$ 与 $\rho$ 的定义为
\begin{equation}
\begin{aligned}
& \boldsymbol{\mathbf{J}} =\sigma \boldsymbol{\mathbf{E}} ,\quad \sigma= \begin{pmatrix}
\sigma_{xx} & \sigma_{xy}\\
-\sigma_{yx} & \sigma_{yy}
\end{pmatrix}
~,\\
& \boldsymbol{\mathbf{E}} =\rho \boldsymbol{\mathbf{J}} ,\quad \rho = \sigma^{-1} =
\begin{pmatrix}\rho_{xx}&\rho_{xy}\\-\rho_{yx} & \rho_{yy}\end{pmatrix} ~,\\
& \boldsymbol{\mathbf{E}} = \begin{pmatrix}E_x\\ E_y\end{pmatrix} ,\quad \boldsymbol{\mathbf{J}} = \begin{pmatrix}J_x\\J_y\end{pmatrix} ~.
\end{aligned}
\end{equation}
霍尔效应表明材料可能存在横向的电阻 $\rho_{xy}$,即如果我们通 $x$ 方向的电流,材料 $y$ 方向会产生霍尔电势差。
Drude 模型中,在电场作用的驱动下,材料中的自由电子会往一个方向加速运动,并有一定的几率撞到离子实被弹回。根据式 20 ,我们可以将电子的运动方程改写为
\begin{equation}
m \frac{\mathrm{d}{ \boldsymbol{\mathbf{v}} }}{\mathrm{d}{t}} = -e(E+ \boldsymbol{\mathbf{v}} \times \boldsymbol{\mathbf{B}} )-\frac{m \boldsymbol{\mathbf{v}} }{\tau} ~.
\end{equation}
其中方程右边的第二项为线性摩擦项,$\tau$ 被称为散射时间,是单个电子相邻两次碰撞间隔的平均时间。
可以将上式对所有自由电子求平均,这样 $ \boldsymbol{\mathbf{v}} $ 理解为材料中自由电子的宏观平均速度,当电场驱动下平均速度不再随时间变化,那么体系达到了平衡态,可以求出平衡状态下材料的电流密度 $ \boldsymbol{\mathbf{J}} =-ne \boldsymbol{\mathbf{v}} $ 与 $ \boldsymbol{\mathbf{E}} $ 的关系。
\begin{equation}
\quad e \boldsymbol{\mathbf{v}} \times \boldsymbol{\mathbf{B}} + \frac{m \boldsymbol{\mathbf{v}} }{\tau} = -eE~.
\end{equation}
设磁场为 $z$ 方向,取电场与电流方向所在的平面为 $xy$ 平面。那么
\begin{equation}
\begin{pmatrix}
m/\tau & {eB}\\
-eB & m/\tau
\end{pmatrix}
\cdot
\begin{pmatrix}v_x\\v_y\end{pmatrix} = \begin{pmatrix}-eE_x \\ -eE_y\end{pmatrix}
~.
\end{equation}
将 $ \boldsymbol{\mathbf{J}} =-ne \boldsymbol{\mathbf{v}} $ 带入,
\begin{equation}
\begin{pmatrix}
1 & eB\tau/m \\
-eB\tau/m & 1
\end{pmatrix}
\cdot
\begin{pmatrix}
J_x\\
J_y
\end{pmatrix} =
\frac{ne^2 \tau}{m }
\begin{pmatrix}
E_x\\
E_y
\end{pmatrix}
~.
\end{equation}
定义电子在磁场中的回旋频率为
\begin{equation}
\omega_B=\frac{eB}{m}~.
\end{equation}
那么
\begin{equation}
\begin{aligned}
& \boldsymbol{\mathbf{E}} =\rho \boldsymbol{\mathbf{J}} ,\quad \rho=\frac{m}{ne^2\tau} \begin{pmatrix}1 & \omega_B\tau \\ -\omega_B\tau & 1\end{pmatrix} ,
\\
& \boldsymbol{\mathbf{J}} =\sigma \boldsymbol{\mathbf{E}} ,\quad \sigma =\frac{ne^2\tau}{m} \frac{1}{1+\omega_B^2\tau^2} \begin{pmatrix}1 & -\omega_B \tau \\ \omega_B \tau & 1\end{pmatrix} ~,\\
&\qquad \qquad\quad =\sigma_{DC} \cdot \frac{1}{1+\omega_B^2\tau^2} \begin{pmatrix}1 & -\omega_B \tau \\ \omega_B\tau &1\end{pmatrix} ~.
\end{aligned}
\end{equation}
其中
\begin{equation}
\sigma_{DC} = \frac{ne^2\tau}{m}~.
\end{equation}
为不加磁场时材料的直流电导率,它正比于自由电子密度。电导率张量为对角矩阵,意味着没有横向的电导。
从电阻率张量中可以看出,对角元即纵向电阻与磁场的大小无关
\begin{equation}
\rho_{xx}=\rho_{yy}=\frac{1}{\sigma_{DC}} ~.
\end{equation}
而非对角元随着磁场的增大而增大,材料的横向电阻率正比于电导率:
\begin{equation}
\rho_{xy}=-\rho_{yx} = \frac{1}{\sigma_{DC}}\cdot \omega_B\tau=\frac{\omega_B m}{ne^2}=\frac{B}{ne}=BR_H~.
\end{equation}
与
式 7 的计算结果一致,横向电阻与磁场的大小成正比。
有趣的是我们利用 drude 模型推出的霍尔电阻率与散射时间 $\tau$ 无关,霍尔电阻率是材料的某种基本的特征,而且与内部混乱的散射无关!
Drude 模型的局限性
当磁场强到一定程度,电子回旋频率 $\omega_B=eB/m$ 较大,这使电子的回旋半径较小,往往局限在某个小区域内运动。此时电子的量子效应将对材料的性质有许多方面的影响,导致量子霍尔效应4等许多新奇物理现象,不再能利用 Drude 模型的经典图像来解释了。
1. ^ 参考 Wikipedia 相关页面。
2. ^ 载流子指可以自由移动的带有电荷的物质微粒。
3. ^ 这里电阻率的定义与式 2 中的纵向电阻的定义不同。
4. ^ 可以参考笔记量子霍尔效应。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。