重积分的换序（简明微积分）

贡献者： addis

预备知识　重积分

　　¹以矩形区域的二重定积分为例，什么时候可以交换积分的顺序呢？即

\begin{equation} \int_{y_1}^{y_2}\int_{x_1}^{x_2} f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} = \int_{x_1}^{x_2}\int_{y_1}^{y_2} f(x, y) \,\mathrm{d}{y} \,\mathrm{d}{x} ~. \end{equation}

乍看之下，二重积分是函数曲面下面的体积，无论先算哪个都不会变。但我们来看一个例子

例 1　

\begin{equation} f(x, y) = \frac{x - y}{(x+y)^3}~. \end{equation}

图 1：式 2 函数曲面图

　　该函数在 $(0,0)$ 处有一个奇点，即没有定义。但是 $x \in (0, 1]$，$y \in (0, 1]$ 的重积分仍然收敛

\begin{equation} \int_0^1 \int_0^1 f(x,y) \,\mathrm{d}{x} \,\mathrm{d}{y} = -\frac{1}{2}~, \qquad \int_0^1 \int_0^1 f(x,y) \,\mathrm{d}{y} \,\mathrm{d}{x} = \frac{1}{2}~. \end{equation}

注意交换顺序以后发现结果竟然不同！

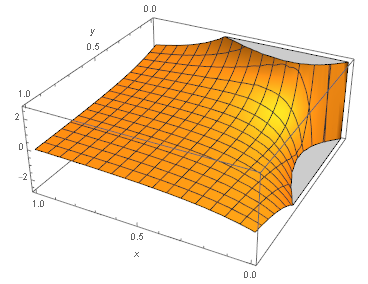
　　观察图 1 会发现，函数曲面关于积分区域的正方形的对角线 $x=y$ 反对称，也就是对角线的下半三角形的区域中函数值为负，上半三角形函数值为正。且函数在 $x$ 轴和 $y$ 轴靠近原点的地方分别出现了无穷大和无穷小。所以 “曲面下的体积” 是否能取有限值（收敛），取决于无穷大和无穷小是否能在积分过程中抵消。

　　为了更好理解，我们不妨延正方形的两个对角线方向分别进行积分，即令

\begin{equation} u = (x+y)/\sqrt{2}~, \qquad v=(x-y)/\sqrt{2} \end{equation}

那么令

\begin{equation} g(u,v) = f(x(u,v), y(u,v)) = \frac{v}{2u^3}~. \end{equation}

该函数表示同一个形状的曲面，我们可以把这看作是把原来的直角坐标系绕 $z$ 轴旋转了 45°。所以如果先对 $v$ 积分再对 $u$ 积分，根据函数曲面的反对称性可以断定对 $v$ 的积分为恒零（对于 $u\ne 0$），那么再把 $u$ 从大到小积分，那么结果也还是零。所以现在我们得到了第三个积分结果——零。而如果先对 $u$ 积分再对 $v$ 积分，那么这就相当于我们先计算 $x=y$ 分割出的一个三角形的体积（负无穷），再计算另一个三角形的体积（正无穷）。这就类似于做定积分 $\int_{-\infty}^{+\infty}1/v \,\mathrm{d}{v} $，你可以认为它不收敛，但在主值积分的定义下，其结果也可以是零。

　　所以现在我们看到曲面下方的体积完全取决于我们采用哪两个方向积分。如果积分的过程中刚好可以把正无穷和负无穷实时抵消，那么积分结果就是有限值甚至是零，且值的大小取决于具体抵消的方式。如果上面的坐标旋转变换使用其他角度，还会得到许多其他不同的值。

定理 1　

　　对多重黎曼积分，如果被积函数是绝对值可积的，那么积分结果与积分变量的次序无关。

　　定理 1 是数学分析中 Fubini 定理的一个特殊应用，Fubini 定理的完整形式和证明超出了本文的范围，将在数学分析中介绍

　　套用在例 1 中，我们需要看看 $ \left\lvert x-y \right\rvert /(x+y)^3$ 的积分是否是有限的。容易验证积分结果是 $+\infty$，所以并不能保证换序积分结果不变。过程留做习题。

1. ^ 参考 Wikipedia 相关页面相关页面。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。