贡献者: _Eden_
1. 克拉伯龙方程
单元系两相平衡共存时,必须满足式 5 的 $T^\alpha=T^\beta=T,P^\alpha=P^\beta=P,\mu^\alpha(T,P)=\mu^\beta(T,P)$ 三个条件。其中相平衡条件中摩尔化学势 $\mu$ 可以看作是温度和压强的函数。此时,相变温度 $T$ 对应着压强 $P$(在压强 $P$ 的环境下,相变温度为 $T$)。
现在考虑系统的温度和压强有改变量 $ \,\mathrm{d}{T} , \,\mathrm{d}{P} $,要使得两相仍处于平衡条件,就有
\begin{align}
&\mu^\alpha(T,P)=\mu^\beta(T,P)~,\\
&\mu^\alpha(T+ \,\mathrm{d}{T} ,P+ \,\mathrm{d}{P} )=\mu^\beta(T+ \,\mathrm{d}{T} ,P+ \,\mathrm{d}{P} )~.
\end{align}
由于化学势就是摩尔吉布斯函数,所以 $ \,\mathrm{d}{\mu} =-S_m \,\mathrm{d}{T} +V_m \,\mathrm{d}{P} $($S_m$ 为摩尔熵,$V_m$ 是摩尔体积)。由 $ \,\mathrm{d}{\mu} ^\alpha= \,\mathrm{d}{\mu} ^\beta$ 可以推出
\begin{equation}
\frac{ \,\mathrm{d}{P} }{ \,\mathrm{d}{T} }=\frac{S^\beta_m-S^\alpha_m}{V^\beta_m-V^\alpha_m}~.
\end{equation}
在实验上熵是不能直接测量的,但我们知道在可逆过程中 $\Delta Q=T\Delta S$。考虑 $1\rm mol$ 物质从 $\alpha$ 相转变到 $\beta$ 相所吸收的相变潜热,由于相变时物质温度不变,有 $L=T(S_m^\beta-S_m^\alpha)$。可以得到克拉伯龙方程:
\begin{equation}
\frac{ \,\mathrm{d}{P} }{ \,\mathrm{d}{T} }=\frac{L}{T(V^\beta_m-V^\alpha_m)}~.
\end{equation}
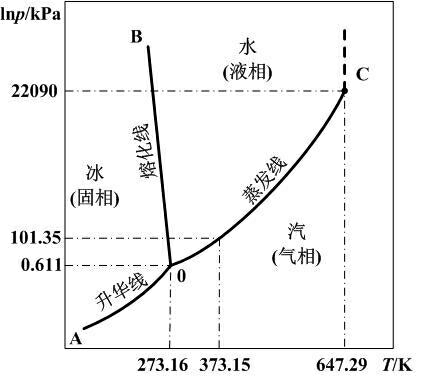
图 1:水的三相图
相平衡曲线的斜率通常是正的,但也存在例外:从水的三相图中看到,水的熔化线斜率 $ \,\mathrm{d}{p} / \,\mathrm{d}{T} <0$。而水的摩尔体积比冰的摩尔体积小,密度比冰大,代入克拉伯龙方程确实能得到熔化曲线斜率小于 $0$ 的结果。
2. 饱和蒸气压方程
由克拉伯龙方程可以得出在气相 $\beta$ 与凝聚相(液相或固相)$\alpha$ 之间的相变方程,可以得到饱和蒸气压与温度的关系,也就是饱和蒸气压方程。现在做粗略的近似,如果将气相看作理想气体,那么由 式 4 可得
\begin{equation}
\frac{1}{P}\frac{ \,\mathrm{d}{P} }{ \,\mathrm{d}{T} }=\frac{L}{RT^2}~.
\end{equation}
再做更粗糙的近似,将相变潜热 $L$ 认为是与温度无关。那么可以积分得:
\begin{equation}
\ln P=-\frac{L}{RT}+A~.
\end{equation}
3. 二级相变的爱伦费斯特方程
爱伦费斯特(Ehrenfest)试图对相变进行分类:因为 $S_m=\frac{\partial \mu}{\partial T},V_m=\frac{\partial \mu}{\partial P}$,爱氏将一级相变概括为化学势连续、但化学势的一级偏导数在两相存在突变的相变。对与这一类相变,$S_m^\alpha\neq S_m^\beta,V_m^\alpha\neq V_m^\beta$,克拉伯龙方程适用。。
但在气液通过临界点的转变、铁磁顺磁的转变等过程中,既没有 $S_m$ 的突变(也就是说不存在相变潜热),又没有 $V_m$ 的突变。在这些过程中,化学势的一级偏导数连续,但化学势的二级偏导数不连续。爱氏将它归类为二级相变。
\begin{align}
&C_{P,m}=T\left(\frac{\partial S_m}{\partial T}\right)=-T\frac{\partial^2 \mu}{\partial T^2}~,\\
&\alpha=\frac{1}{V_m}\left(\frac{\partial V_m}{\partial T}\right)_P
=\frac{1}{V_m}\frac{\partial^2\mu}{\partial T\partial P}~,\\
&\kappa_T=-\frac{1}{V_m}\left(\frac{\partial V_m}{\partial P}\right)_T
=-\frac{1}{V_m}\frac{\partial^2\mu}{\partial P^2}~.
\end{align}
对于二级相变,容易得出压强与温度的新变化关系,爱伦费斯特方程:
\begin{equation}
\frac{ \,\mathrm{d}{P} }{ \,\mathrm{d}{T} }=\frac{\alpha^{(2)}-\alpha^{(1)}}{\kappa_T^{(2)}-\kappa_T^{(1)}}=\frac{C_{P,m}^{(2)}-C_{P,m}^{(1)}}{TV_m(\alpha^{(2)}-\alpha^{(1)})}~.
\end{equation}
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。