相机模型

贡献者： addis

本文处于草稿阶段。

预备知识　三维投影，图片坐标系

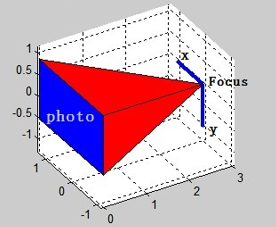
图 1：相机坐标系

　　从焦点出发，穿过底片并与底片垂直的射线叫做光轴。

　　以焦点为原点，光轴方向为 $z$ 轴，图片的右方为 $x$ 轴，下方为 $y$ 轴（注意这是常用的右手系）。

　　真实的相机和这里的相机模型存在误差，通常需要将图片进行纠偏后才能得到符合模型的图像。以后我们讨论的图像一般指纠偏后的图像。

　　注意图像的中点不一定是光轴和底片的交点。

　　相机参数：焦距，底片宽度，底片高度，光轴的图像坐标

　　相机的位置参数：焦点的位置，三个单位矢量在世界坐标系中的坐标（即旋转矩阵，也可以使用四元数表示）

　　反过来，若已知图片和相机位置和参数，我们可以将图片上的每一点对应到以相机为起点的一条射线。而至于这点具体在射线上的什么位置无从得知。但如果我们从两个不同的位置拍摄同一点，就可以通过两条射线的交点确定该点位置。

　　若已知相机参数，我们可以通过图片中的任意两点确定它们关于相机的夹角（即两条射线的夹角）。

1. 变换方程

　　变换有 7 个自由度，相机位置 3 个，相机角度 3 个，相机焦距 1 个。

　　一般形式为（推导：根据相机模型结合立体几何）

\begin{equation} \left\{\begin{aligned} x' &= \frac{c_4 x + c_5 y + c_6 z + c_7}{c_1 x + c_2 y + c_3}\\ y' &= \frac{c_8 x + c_9 y + c_{10} z + c_{11}}{c_1 x + c_2 y + c_3} \end{aligned}\right. ~ \end{equation}

注意这里的 9 个常系数中只有 7 个是独立的。所以理论上我们可以只用 4 个一般位置的点及它们在图片上的坐标解得所有的系数，但这样方程就不是线性的了。所以我们也可以假设 9 个系数都是独立的，并用 6 个或以上一般位置的点得到 12 条（或以上）关于 $c_i$ 的超定齐次线性方程组，并利用超定来减小误差。

　　如果我们不仅需要得到变换公式，还需要从这些系数里面得到相机的位置和朝向，那么我们可以从立体几何的角度出发，例如见长方形相机定位法。但这样我们需要的 4 个点就必须是长方形的四个顶点而不是任意点。

2. 平面到平面的变换

　　注意式 1 不存在逆变换，因为我们把空间中的点投影到平面上时丢失了景深的信息。但如果我们限制所有空间点 $(x, y, z)$ 都在某个平面上（不失一般性，假设它们在 $x$-$y$ 平面上），那两个平面上的点就有一一对应的关系。

\begin{equation} \left\{\begin{aligned} x' &= \frac{c_4 x + c_5 y + c_6}{c_1 x + c_2 y + c_3}\\ y' &= \frac{c_7 x + c_8 y + c_9}{c_1 x + c_2 y + c_3} \end{aligned}\right. ~ \end{equation}

可以证明其逆变换也有相同的形式，虽然这并不显然。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。