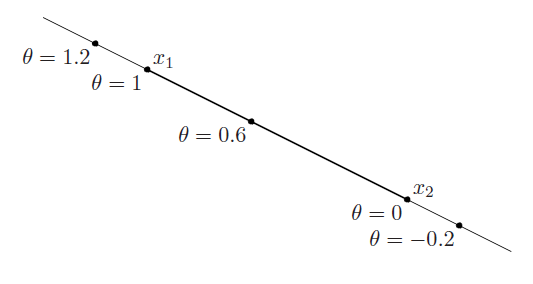贡献者: Giacomo; 零穹; xzllxls
仿射集是矢量空间中的一类子集,它起源于线性代数和几何学的共同发展。它是研究向量空间中点的集合性质的一种方式。在更广泛的背景下,其所对应的仿射几何已经成为几何学的一个重要分支。本文将介绍其基本概念和一些相关的定理。
定义 1 仿射组合与仿射集
取向量空间 $V$ (记其域为 $\mathbb{F}$) 中的两点 $x_1, x_2 \in V$ 的线性组合 $\theta x_1 + (1 - \theta) x_2$ 被称为 $x_1, x_2$ 的仿射组合;更一般的,系数和为一(即 $\sum_i a_i = 1$)的线性组合 $\sum_i a_i x_i$ 被称为 $x_1, \dots, x_n$ 的仿射组合。
向量空间的子集 $C \subseteq V$ 被称为仿射集(affine set),意味着 $C$ 中的任意仿射组合都在 $C$ 中;等价的,我们只需要考虑任意两个向量的仿射组合即可(和向量子空间的情况一样)。
图 1:仿射集示意图
图 $1$ 表示的是一条穿过 $x_1,x_2$ 两点的直线。当 $0 \leq \theta \leq 1$,形成图中直线加粗的部分;反之,形成直线上细线表示的部分。
从几何上看,仿射集仍然是平直的,或者说 “线性的”:
定理 1
对任意的仿射集 $C \subseteq V$,存在唯一的向量子空间 $U \subseteq V$,使得对任意的 $x \in C$,我们有
\begin{equation}
C = x + U = \{ x + v \mid v \in U\}~.
\end{equation}
证明:第一步,取一点 $x_0 \in C$,我们定义
\begin{equation}
U: = \{ x - x_0 \mid x \in C \}~,
\end{equation}
要证明它是一个向量子空间:
- $0_V = x_0 - x_0 \in U$,
- 对任意的 $a, b \in \mathbb{F}$,$x, y \in C$,
\begin{equation}
\begin{aligned}
a (x - x_0) + b (y - x_0) &= a x + b y - (a + b - 1) x_0 - x_0 \\
&= a x + b y + (1 - (a + b)) x_0 - x_0 \\
\end{aligned}~
\end{equation}
第二步,要证明对任意的 $x \in C$,$C = x + U$:首先证明 $\subseteq$,对任意的 $y \in C$,我们有
\begin{equation}
y = x + (y - x_0) - (x - x_0); ~
\end{equation}
现在证明 $\supseteq$,对任意的 $u = z - x_0 \in U$,我们有
\begin{equation}
x + u = x + z + (-1) x_0 ~
\end{equation}
是 $x, z, x_0$ 得仿射组合,证得。
第三步,要证明 $U$ 不依赖于 $x_0$ 的选取——对任意的 $x' \in C$,定义 $U': = \{x - x' \mid x \in C\}$,我们要证明 $U' = U$,处于对称性我们只需要证明 $U' \subseteq U$:取 $x \in C$,
\begin{equation}
x - x' = (x + x_0 - x') - x_0 ~
\end{equation}
$x + x_0 - x'$ 是 $x, x_0, x'$ 的仿射组合,因此证得。
第四步,证明 $U$ 的唯一性:假设 $V$ 存在另外一个向量子空间 $U'$ 满足对任意 $x \in C$,$C = x + U'$,取 $x = x_0$,那么 $x_0 + U' = x_0 + U \implies U' = U$。
证毕!
因此我们可以定义仿射集的维度
定义 2 维度
对于仿射集 $C \subseteq V$,我们定义它的维度为它对应的向量空间的维度。
特别的,一维的仿射集被称为仿射直线,二维的被称为仿射平面,余一维的被称为仿射超平面。
在向量空间中谈直线、平面、超平面时,我们有时指的是向量子空间,有时指的是仿射子空间,要注意分辨。
定理 2
对于向量空间的子集 $C \subseteq V$,$C$ 为仿射集当且仅当过 $C$ 中任意不同的两点的(仿射)直线仍然在 $C$ 中。
证明:必要性:假设 $C$ 是仿射集。那么任意由 $x_1,x_2\in C$ 确定的直线为 $x_1+(1-k)x_2,k\in\mathbb F$,即是 $x_1,x_2$ 的仿射组合,因此由仿射集的定义(定义 1 ),该直线属于 $C$。
充分性:设 $C$ 是过其上任意两点的直线都在 $C$ 中的集。那么任意 $x_i\in C,i=1,\cdots ,n$,对任意满足 $\sum_{i}a_i=1$ 的 $a_i\in\mathbb F$,成立(不失一般性,设 $a_1\neq1$)
\begin{equation}
\sum_{i=1}^n a_ix_i=(1-a_1)\sum_{i=2}^n \frac{a_i}{1-a_1}x_i+a_1x_1~.
\end{equation}
设 $n-1$ 时充分性成立。那么 $\sum_{i=2}^n \frac{a_i}{1-a_1}x_i\in C$,又
式 7 是 $\sum_{i=2}^n \frac{a_i}{1-a_1}x_i$ 和 $x_1$ 的仿射组合,因此 $\sum_{i=1}^n a_ix_i\in C$,即 对 $n$ 时充分性成立。根据数学归纳法和仿射集的定义,$C$ 是仿射集。
证毕!
推论 1
设 $U\subset V$ 是线性空间 $V$ 的子空间,$x\in V$,则 $x+U$ 是仿射集。
证明:任意 $x_1,x_2\in x+U$,设 $x_1=x+y_1,x_2=x+y_2$,其中 $y_1,y_2\in U$。则过 $x_1,x_2$ 的直线为
\begin{equation}
\{x_1+k(x_2-x_2)|k\in\mathbb F\}=\{x+(y_1+k(y_2-y_1))|k\in\mathbb F\}\subset x+U~.
\end{equation}
因为 $x_1,x_2$ 任意,所以由
定理 2 ,命题得证!
证毕!
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。