有限深不对称方势阱

贡献者：零穹; addis

本文存在未完成的内容。
需要讨论散射态，即 $E > V_1$ 的两种情况

预备知识　有限深方势阱

图 1：一维不对称势阱

　　本节我们来解下面的一维不对称势阱的离散谱（图 1 ）。

\begin{equation} V(x)=\left\{\begin{aligned} &V_1\quad(x<0)\\ &0\quad (0< x< L)\\ &V_2\quad(x>L) \end{aligned}\right. ,\qquad (V_1 < V_2)~. \end{equation}

对于离散谱，能量 $E$ 需小于无穷远处势能，故 $E< V_1$.

　　在 $x<0$ 区域内的其薛定谔方程为

\begin{equation} \frac{\hbar^2}{2m} \frac{\mathrm{d}^{2}{\psi(x)}}{\mathrm{d}{x}^{2}} +(E-V_1)\psi(x)=0~. \end{equation}

满足边界条件 $\psi(-\infty)\to 0$ 的波函数为

\begin{equation} \psi(x)=C_1 e^{\kappa_1 x},\quad \kappa_1=\frac{1}{\hbar}\sqrt{2m(V_1-E)}~. \end{equation}

　　在 $x>L$ 区域内的其薛定谔方程为

\begin{equation} \frac{\hbar^2}{2m} \frac{\mathrm{d}^{2}{\psi(x)}}{\mathrm{d}{x}^{2}} +(E-V_2)\psi(x)=0~. \end{equation}

满足边界条件 $\psi(+\infty)\to 0$ 的波函数为

\begin{equation} \psi=C_2 e^{-\kappa_2 x},\quad \kappa_2=\frac{1}{\hbar}\sqrt{2m(V_2-E)}~. \end{equation}

　　在阱内 $0 < x < L$，薛定谔方程为

\begin{equation} \frac{\hbar^2}{2m} \frac{\mathrm{d}^{2}{\psi(x)}}{\mathrm{d}{x}^{2}} +E\psi(x)=0~. \end{equation}

$\psi$ 可取以下形式：

\begin{equation} \psi=C \sin\left(kx+\delta\right) ,\quad k=\frac{\sqrt{2mE}}{\hbar}~. \end{equation}

　　根据势阱边上 $\psi'/\psi$ 的连续性条件，得

\begin{equation} k\cot\delta=\kappa_1=\sqrt{\frac{2m}{\hbar^2}V_1-k^2},\quad k \cot\left(Lk+\delta\right) =-\kappa_2=-\sqrt{\frac{2m}{\hbar^2}V_2-k^2}~, \end{equation}

或

\begin{equation} \sin\delta=\frac{k\hbar}{\sqrt{2mV_1}},\quad \sin\left(kL+\delta\right) =-\frac{k\hbar}{\sqrt{2mV_2}}~. \end{equation}

消去 $\delta$ 后，得下列超越方程：

\begin{equation} kL=n\pi-\arcsin\frac{k\hbar}{\sqrt{2mV_1}}-\arcsin\frac{k\hbar}{\sqrt{2mV_2}}~. \end{equation}

其中，$k=1,2,3,\cdots$，反正弦函数取值介于 $0$ 到 $\pi/2$ 之间。上式之根确定了能级 $E=k^2\hbar^2/2m$。对每一个 $n$ 一般来讲只有一个根；$n$ 值按能级的递增次序编号。其左右两边的图像大致如图 2 .

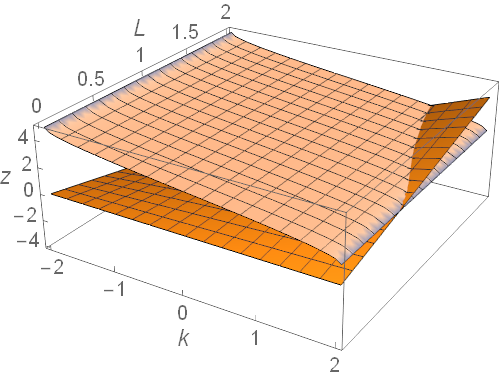
图 2：式 11 左右两式对应的函数图像（上层浅红色代表右式，下层浅橘色代表左式），其中 $\frac{\hbar}{\sqrt{2mV_1}}=0.5,\frac{\hbar}{\sqrt{2mV_2}}=0.1,n=1$

　　由于反正弦函数宗量不能超过 1，$k$ 值显然只能介于 $0$ 到 $\sqrt{2mV_1}/\hbar$ 之间。式 10 左边随 $k$ 单调增加，右边却随 $k$ 单调减小。因此式 10 有根的必要条件为 $k=\sqrt{2mV_1}/\hbar$ 时，式 10 右边小于左边。特别是，由 $n=1$ 所得的下列不等式

\begin{equation} L\frac{\sqrt{2mV_1}}{\hbar}\geq\frac{\pi}{2}-\arcsin\sqrt{\frac{V_1}{V_2}}~. \end{equation}

给出了阱中至少存在一个能级的条件。由此可见，给定了不相等的 $V_1$ 和 $V_2$ 后，总可以找到一个很窄的阱宽 $L$，使得该阱中不能存在离散能级，图 2 中可看出在 $0< L<0.5$ 处式 11 无解。对 $V_1=V_2$ 而言，式 11 总能得到满足。

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。