贡献者: _Eden_; addis
对称性在一个量子场论的理论中具有非常重要的作用,例如时空平移对称性使得我们能够在动量表象下研究散射过程的振幅,洛伦兹对称性保证了 Feynman 矩阵元也具有洛伦兹对称性。而现在我们研究规范对称性的一个重要推论——Ward-Takahashi 等式,简称 Ward 等式。
图 1:Ward 等式示意图
1. 费曼图层面的证明
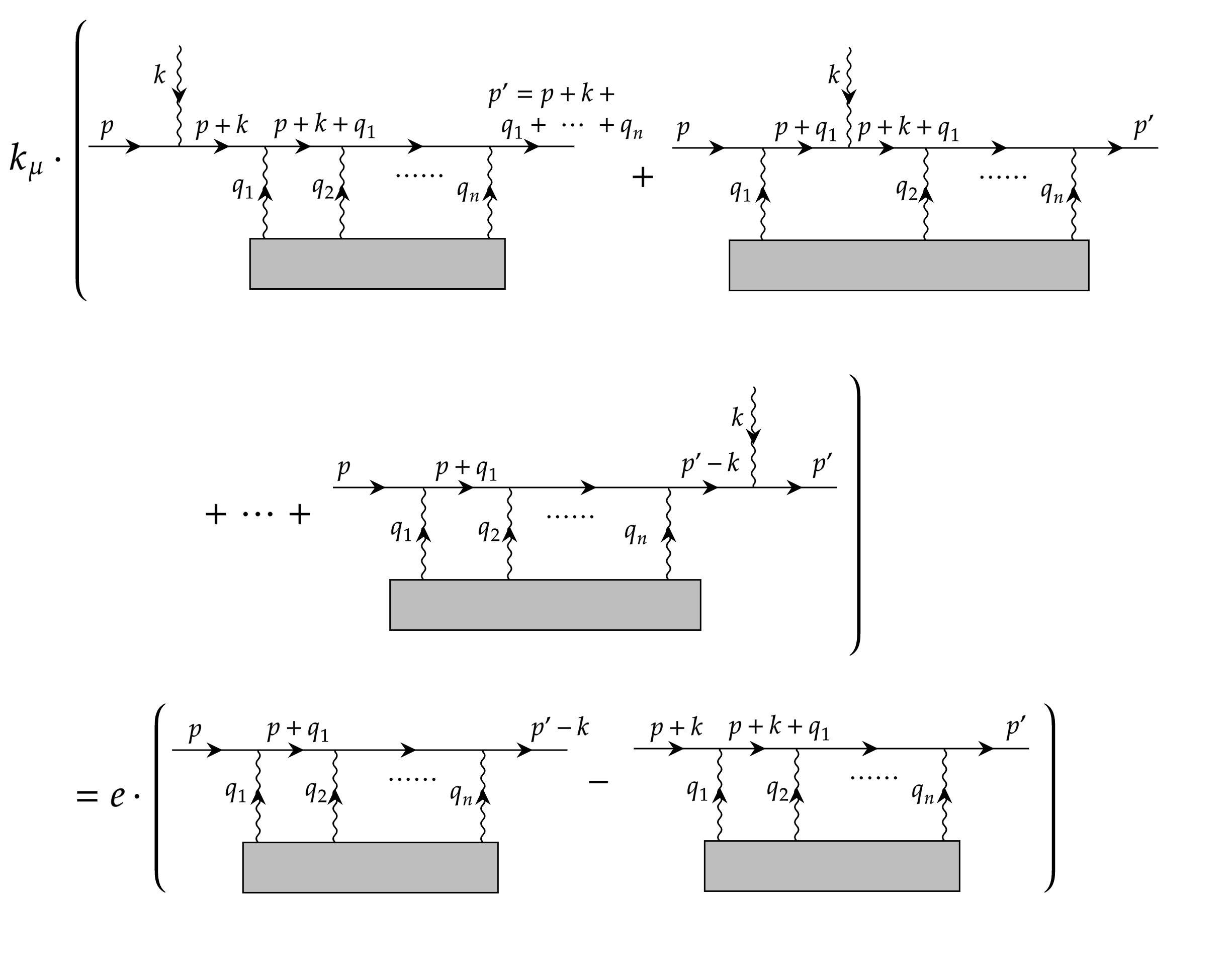
Ward 等式的费曼图表达式如上图所示,假设动量为 $k$ 的光子线的一端可以接在一条费米子链上的任意位置(还有一种情况是光子线接在费米子圈上,这种情况我们在后面会讨论);这条费米子链从动量为 $p$ 的费米子传播子出发,到动量为 $p'=p+k+q_1+\cdots+q_n$ 的费米子传播子结束。费曼图中所有这些光子可以在壳,也可以不在壳(即可以是虚光子)。并且当我们在计算动量 $k$ 光子线插入某个位置时的费曼图贡献时,用 $k_\mu$ 来代替 $\epsilon_\mu(k)$ 进行缩并。在这里费米子链两端的费米子线我们不将它们看作是散射过程的外线,而是看成是某个费米子传播子,那么其中第 $i+1$ 个费曼图的贡献计算如下
\begin{equation}
\begin{aligned}
&\quad F_i\\
&=k_\mu\cdot \frac{i}{\not p'-m}\cdots\\
&\quad (-ie\gamma_{\mu_{i+1}})\frac{i}{\not p+\not k+\not q_1+\cdots+\not q_i-m}
(-ie\gamma_\mu)
\frac{i}{\not p+\not q_1+\cdots+\not q_i - m}(-ie\gamma_{\mu_i})\cdots \frac{i}{\not p - m}
\\
&=
e\left(\frac{i}{\not p'-m}\cdots(-ie\gamma_{\mu_{i+1}})\frac{i}{\not p+\not q_1\cdots + \not q_i - m}(-ie\gamma_{\mu_i})\cdots \frac{i}{\not p-m}+\right.\\
&\quad-\left.\frac{i}{\not p'-m}\cdots(-ie\gamma_{\mu_{i+1}})\frac{i}{\not p+\not k+\not q_1+\cdots + \not q_i-m}(-ie\gamma_{\mu_i}) \cdots \frac{i}{\not p-m}\right)
\\
&=e(A_{i+1}-A_i)~.
\end{aligned}
\end{equation}
其中我们将 $\not k$ 替换为了 $(\not p+\not k+\not q_1+\cdots + \not q_i-m) - (\not p+\not q_1+\cdots + \not q_i-m)$ 再进行通分,最终得到了上面的结果。其中 $A_i$ 所对应的表达式中,$\not k$ 出现在 $(-ie\gamma_{\mu_{i}})$ 前面所有的传播子分母里。因此,将光子插在费米子链各个位置的所有的 Feynman 图相加后,最终可以得到
\begin{equation}
k_\mu (\cdots) = \sum_{i=0}^n F_i = e[A_{n+1}-A_0]~.
\end{equation}
经过上面的分析,我们已经初步证明了 Ward 等式的一般形式。若费米子链两端不是在壳的费米子外线,而是当作费米子传播子来计算其贡献,我们只能得到
式 2 ,其中 $A_{n+1}$ 中两端费米子线的动量为 $p'-k,p$,而 $A_{0}$ 中两端费米子线的动量为 $p',p+k$。因此
式 2 的结果可以简记为
\begin{equation}
k_\mu\mathcal{M}^\mu(k,p,p') = e(\mathcal{M}(p,p'-k)-\mathcal{M}(p+k,p'))~.
\end{equation}
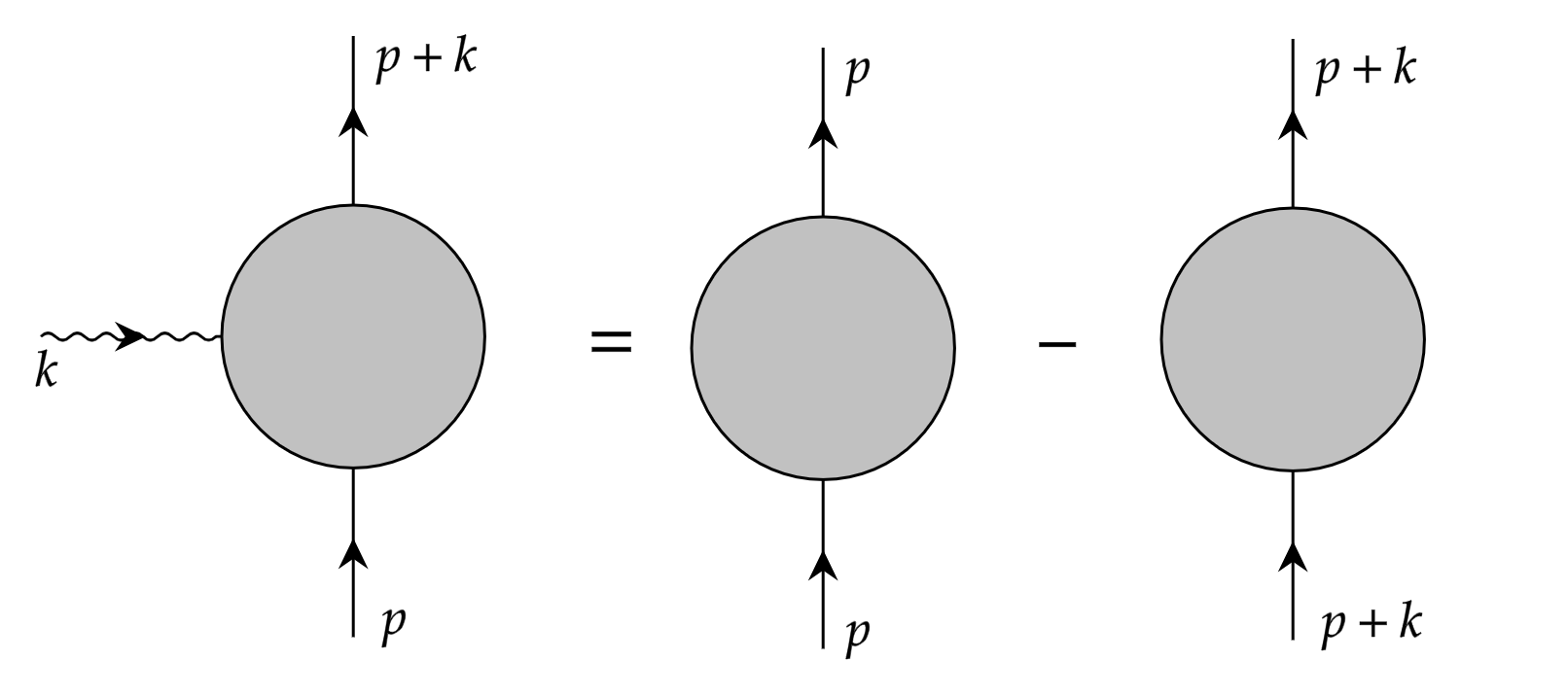
当费曼图中只有一条费米子链或只有两条费米子外线时,Ward 等式可以表示为
图 2:Ward 等式示意图
其中阴影区域是任意可能的费曼图贡献之和。若有多条费米子链,由于光子 $k$ 可以接在任意一条费米子链上,所以 Ward 等式为
\begin{equation}
\begin{aligned}
& \quad k_\mu\mathcal{M}^\mu(k,p_1,\cdots,p_n;p'_1,\cdots,p'_m) \\
& = e\left(
\mathcal{M}(p_1,\cdots p_n;p'_1-k,\cdots p'_m)+\cdots+\mathcal{M}(p_1,\cdots p_n;p'_1,\cdots p'_m-k)
\right.
\\
&\quad \left.-\mathcal{M}(p_1+k,\cdots,p_n;p'_1,\cdots,p'_m)-\cdots-\mathcal{M}(p_1,\cdots,p_n+k;p'_1,\cdots,p'_m)
\right)~.
\end{aligned}
\end{equation}
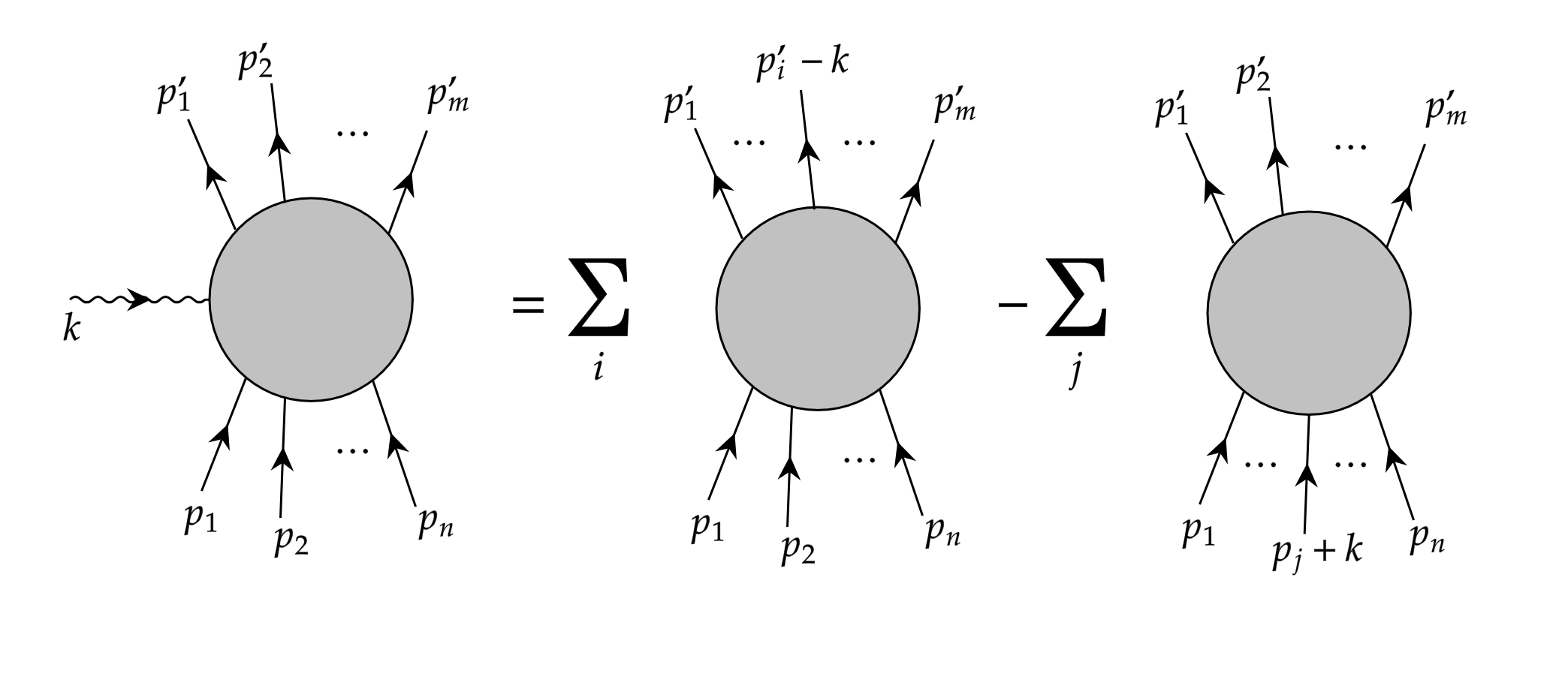
用费曼图可以表示为
图 3:Ward 等式示意图
费米子外线在壳的情况
现在考虑费米子链的两端是在壳的费米子外线的情况。由于外腿在壳时存在极点行为,如果我们要考察散射振幅,根据 LSZ 约化公式,我们需要取其中最奇异的多极点部分。那么外线对应的是费米子旋量 $\bar u(p')$ 和 $u(p)$:
\begin{equation}
\begin{aligned}
F_i = k_\mu \cdot \bar u(p')\cdots S(p+k+q_1+\cdots q_i)(-ie\gamma_\mu)S(p+q_1+\cdots + q_i)\cdots u(p)~.
\end{aligned}
\end{equation}
此时 $A_1\cdots A_n$ 在累加的过程中仍然互相抵消,最终得到
式 2 的结果。考虑 $A_{n+1}$ 和 $A_0$,它们分别包含 $\bar u(p')(\not p'-m)$ 和 $(\not p-m)u(p)$,因此 $A_{n+1}=A_0=0$。这个结果告诉我们:对于
费曼图外线为在壳费米子的情况,我们有
\begin{equation}
k_\mu \mathcal{M}^\mu(k) = 0,\quad (\mathcal{M} = \epsilon_\mu(k)\mathcal{M}^\mu(k))~.
\end{equation}
利用这个结果还可以得到许多有趣的结论。设想费曼图中有一条动量为 $p$ 的虚光子线,其两端的指标是 $\mu$ 和 $\nu$,那么该费曼图的贡献可以表示为 $\frac{1}{p^2+i\epsilon}(-ig_{\mu\nu})\cdot\mathcal{M}^{\mu\nu}(p)$。当我们计算 S-矩阵元 或其他可观测量时,我们需要对外线固定的所有可能的费曼图进行求和,所以虚光子线接在费米子链的任意位置都会对答案有贡献。因此根据 Ward 等式,我们有
\begin{equation}
\begin{aligned}
p_\mu \mathcal{M}^{\mu\nu} = p_\nu\mathcal{M}^{\mu\nu}= 0~.
\end{aligned}
\end{equation}
所以如果我们将光子传播子由 $-ig_{\mu\nu}/(p^2+i\epsilon)$ 改为 $\left(g^{\mu\nu}-(1-\xi)\frac{p^\mu p^\nu}{ (p^2+i\epsilon)}\right)\frac{-i}{p^2+i\epsilon}$,对 S-矩阵元的结果没有影响。所以无论是选取 $\xi=1$ 的 Feynman 规范或是其他规范,可观测量的计算结果都是一样的。
光子线接在费米子圈上
我们上面的证明遗漏了一种情况,即动量 $k$ 光子线也可以接在某个费米子圈上。对于这种情况,我们可以证明 $k^\mu \mathcal{M}^\mu=0$,有了这个结论以后式 3 和式 4 的正确性才能被严格证明。
设费米子圈上某一条费米子线动量为 $l$,在求费米子圈的贡献时我们需要对四动量 $l$ 进行积分。从它出发 $q_1,\cdots,q_n$ 依次为费米子圈上的 $n$ 条光子线。令 $p_i=l+\sum_{j=1}^i q_j$,那么当光子 $k$ 夹在动量为 $q_i$ 和 $q_{i+1}$ 的两条光子线之间时,
费米子圈上的动量依次是 $l,p_1,\cdots,p_i,
p_i+k,\cdots,p_n+k=l$。我们可以将费米子线 $l$ 减断,使得费米子圈变成一条费米子链,左右两端费米子线的动量为 $l$ 和 $p_n+k=l$。类似于先前的 Ward 等式的证明,我们有
\begin{equation}
\begin{aligned}
k_\mu \mathcal{M}^\mu(k)&=e[A_{n+1}-A_0] =e[K(p_1,\cdots,p_n)-K(p_1+k,\cdots,p_n+k)]\\
&=e[K(p_1,\cdots,p_n)-K(p_1,\cdots,p_n)]=0~,
\end{aligned}
\end{equation}
这里我们用到了费米子圈积分的振幅在圈动量平移 $l\rightarrow l-k$ 变换下不变。因此我们证明了光子线接在费米子圈上的振幅的贡献之和为 $0$。
2. $Z_1=Z_2$
在电子自能和光子自能的单圈修正中,我们对裸拉氏量中的场量进行缩放得到了重整化的拉氏量
\begin{equation}
\begin{aligned}
\mathcal{L} &= \bar{\psi}_0 (i\not\partial -m_0)\psi_0 -\frac{1}{4}(F_0^{\mu\nu})^2 - e_0\bar\psi_0 \gamma_\mu\psi_0 A_0^\mu
\\
&=Z_2\bar\psi (i\not\partial - m_0)\psi - \frac{1}{4}Z_3 (F^{\mu\nu})^2-e_0Z_2Z_3^{1/2} \bar\psi \gamma^\mu\psi A_\mu\\
&=\bar\psi (iZ_2\not\partial - Z_m m)\psi - \frac{1}{4}Z_3 (F^{\mu\nu})^2-Z_1 e \bar\psi \gamma^\mu\psi A_\mu~.
\end{aligned}
\end{equation}
其中我们重新定义了 $Z_1e=e_0 Z_2 Z_3^{1/3},Z_m m=Z_2 m_0$,$m,e$ 为物理质量和物理电荷。我们可以在适当的重整化条件下确定各个重整化常数。
让我们从 Ward 等式和 QED 的裸拉氏量出发给出 $Z_1=Z_2$ 的一个证明。考虑两条电子外线、一条光子外线所组成的三点函数
\begin{equation}
k_\mu \mathcal{M}^\mu(k,p,p+k)=e_0(\mathcal{M}^{\mu}(p)- \mathcal{M}^{\mu}(k))~.
\end{equation}
利用三点函数 Feynman 规则(
定理 1 ),并且保留电子外线的正规传播子(它有在壳极点行为),并截去光子外线的正规传播子(也就是直接连在截肢图上,这不影响 Ward 等式的正确性,因为只有直接连在截肢图上才能对 $k_\mu \mathcal{M}^\mu$ 有贡献),将光子外线贡献用 $k_\mu$ 替代。我们总是可以将三点函数的 Feynman 图表示为 QED 正规顶点和两条电子外腿图的组合:
\begin{equation}
k_\mu \mathcal{M}^\mu(k,p,p+k) = S(p+k) [-ie_0k_\mu \Gamma^\mu(p+k,p)] S(p) =e_0[S(p)-S(p+k)]~.
\end{equation}
其中
\begin{equation}
S(p)=iZ_2/(\not p-m+i\epsilon)+(\text{regular term at } p^2=m^2)~
\end{equation}
为电子的正规传播子(两点编时格林函数),$Z_2$ 为裸拉氏量的正规传播子在 $\not p=m$ 处的留数。对
式 11 两边除以 $S(p)S(p+k)$,可以得到
\begin{equation}
-ik_\mu \Gamma^\mu(p+k,p) = [S(p+k)^{-1}-S(p)^{-1}]= -i Z_2^{-1}\not k~.
\end{equation}
根据 LSZ 约化公式
,三点函数所对应的 Feynman 振幅为
\begin{equation}
i\mathcal{M} = Z_2(Z_3)^{1/2}\epsilon_\mu(k)\bar u(p+k)[-ie_0\Gamma^\mu] u(p)=\epsilon_\mu(k)\bar u(p+k)[-i e Z_1\Gamma^\mu] u(p)~.
\end{equation}
由于 $|\mathcal{M}|^2$ 是可观测量,且在非相对论极限下,从上式出发应当正确地得到库仑定律。非相对论极限下的计算告诉我们,在 $k\rightarrow 0$ 的极限下,$Z_1 \Gamma^\mu(k=0) = \gamma^\mu$。代入
式 13 ,我们最终得到
\begin{equation}
-i k_\mu Z_1^{-1} \gamma^\mu = -i Z_2^{-1}\not k~,
\end{equation}
因此
\begin{equation}
Z_1=Z_2~.
\end{equation}