一维薛定谔方程不稳定的差分法数值解（Matlab）

贡献者： addis

预备知识　薛定谔方程（单粒子一维），一维波动方程的简单数值解（Matlab）

　　本文使用原子单位制。本文演示如何用差分法解一维薛定谔方程。

\begin{equation} -\frac{1}{2m} \frac{\partial^{2}}{\partial{x}^{2}} \psi + V(x,t)\psi = \mathrm{i} \frac{\partial}{\partial{t}} \psi~. \end{equation}

　　乍看之下，类比 “一维波动方程的简单数值解（Matlab）”，我们似乎也能用简单的差分法求解式 1 ，但事实证明这是行不通的，迭代几步以后，数值误差就会盖过波函数本身。这说明对薛定谔方程来说，差分法是一个不稳定的算法。但为了教学，还是把公式和代码给出来。

　　一些稳定的算法如直接对角化（未完成）、Crank-Nicolson、以及 Lanczos 算法（通常配合 FEDVR 网格一起使用）。

　　把波函数取离散值，令 $\psi_{i,n} = \psi(x_i,t_n)$。用有限差分表示二阶导数（式 5 ），得

\begin{equation} -\frac{1}{2m}\frac{\psi_{i-1,n} - 2\psi_{i,n} + \psi_{i+1,n}}{\Delta x^2} + V_{i,n}\psi_{i,n} = \mathrm{i} \frac{\psi_{i, n+1} - \psi_{i, n}}{\Delta t}~. \end{equation}

于是

\begin{equation} \psi_{i, n+1} = \frac{ \mathrm{i} \Delta t}{2m\Delta x^2} (\psi_{i-1,n} - 2\psi_{i,n} + \Delta t\psi_{i+1,n}) + (1- \mathrm{i} \Delta t V_{i,n})\psi_{i,n}~. \end{equation}

　　失败的差分法程序如下

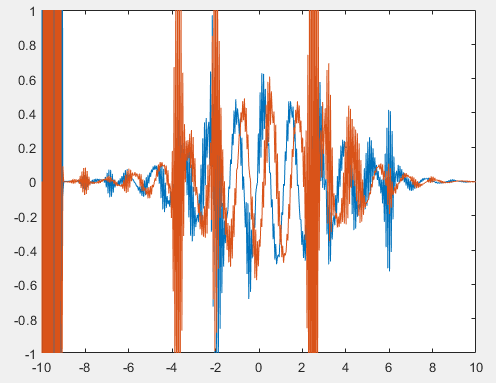
图 1：程序运行的第 24 个循环，噪音已经使波函数扭曲。即使把时间步长和空间步长设置得很小也不会有多大改善。

代码 1：TDSE_1d_failed.m

% 差分法解一维薛定谔方程

function TDSE_1d_failed
% ==== 参数设置 ======
m = 1; % 质量，角频率
xmin = -10; xmax = 30; Nx = 1000; % x 网格
tmin = 0; tmax = 10; Nt = 3000; % 时间网格
Nplot = 1; % 画图步数
t0 = 0; % 高斯波包的初始时间
p0 = 5; % 初始动量
x0 = 0; sig_x = 2; % 初始位置， 波包宽度
V = @(x,t) zeros(size(x));
% ===================
close all;
psi_gs = @(x) 1/(2*pi*sig_x^2)^0.25/sqrt(1 + 1i*t0/(2*m*sig_x^2))...
      *exp(-(x-x0-p0*t0/m).^2/(2*sig_x)^2/(1 + 1i*t0/(2*m*sig_x^2)))...
      .*exp(1i*p0*(x-p0*t0/(2*m)));
x = linspace(xmin, xmax, Nx); dx = (xmax-xmin)/(Nx-1);
t = linspace(tmin, tmax, Nt); dt = (tmax-tmin)/(Nt-1);
psi = psi_gs(x);
figure; plot(x, real(psi)); hold on;
plot(x, imag(psi));
for it = 1:Nt
    d2psi = [0, psi(1:end-2) - 2*psi(2:end-1) + psi(3:end), 0];
    psi = 1i*dt/(2*m*dx^2)*d2psi + (1 - 1i*dt*V(x,t(it))).*psi;
    psi(1) = 0; psi(end) = 0;
    if mod(it, Nplot) == 0
        clf;
        plot(x, real(psi)); hold on;
        plot(x, imag(psi)); axis([xmin,xmax,-0.5,0.5]);
    end
end
end