Crank-Nicolson 算法解一维含时薛定谔方程（Matlab）

                     

贡献者： addis

预备知识 1　薛定谔方程（单粒子一维）

　　1本文使用原子单位制。薛定谔方程为

\begin{equation} -\frac12 \frac{\partial^{2}{\psi}}{\partial{x}^{2}} + V\psi = \mathrm{i} \frac{\partial \psi}{\partial t} ~. \end{equation}
传播子作用于波函数为
\begin{equation} \psi(x,t+\Delta t) = \exp\left(- \mathrm{i} H \Delta t\right) \psi(x,t)~. \end{equation}
用 Crank-Nicolson 或 Caley scheme2 得到的结果是
\begin{equation} \left(1+\frac{ \mathrm{i} }{2} \boldsymbol{\mathbf{H}} _{n+1}\Delta t \right) \boldsymbol{\mathbf{\psi}} _{n+1} = \left(1-\frac{ \mathrm{i} }{2} \boldsymbol{\mathbf{H}} _n\Delta t \right) \boldsymbol{\mathbf{\psi}} _n~. \end{equation}
其中 $ \boldsymbol{\mathbf{\psi}} _n$ 是时刻 $t_n$ 的波函数列矢量（已知），$ \boldsymbol{\mathbf{\psi}} _{n+1}$ 为时刻 $t_{n+1}$ 的波函数列矢量（未知），$ \boldsymbol{\mathbf{H}} _n$ 是 $t_n$ 时刻的哈密顿矩阵。

　　 但事实上，还可以继续减少计算量。若近似认为3 $ \boldsymbol{\mathbf{H}} _{n+1}\approx \boldsymbol{\mathbf{H}} _{n}$，将式 3 整理后得

\begin{equation} \left(\frac12 + \frac{ \mathrm{i} }{4} \boldsymbol{\mathbf{H}} _n\Delta t \right) \left( \boldsymbol{\mathbf{\psi}} _{n+1}+ \boldsymbol{\mathbf{\psi}} _n \right) = \boldsymbol{\mathbf{\psi}} _n~. \end{equation}
解这个方程，再减去 $ \boldsymbol{\mathbf{\psi}} _n$ 即可。

1. 等间距网格

　　 对于等间距坐标网格 $x_1,x_2,\dots$，可以用差分法（式 5 ）计算二阶导数，表示为矩阵有

\begin{equation} \boldsymbol{\mathbf{D}} _2 = \frac{1}{\Delta x^2} \begin{pmatrix}-2 & 1 & 0 & 0 & \dots\\ 1 & -2 & 1 & 0 & \dots\\ 0 & 1 & -2 & 1 & \dots\\ 0 & 0 & 1 & -2 & \dots\\ \vdots & \vdots & \vdots & \vdots & \ddots\end{pmatrix} ~. \end{equation}
那么 $ \boldsymbol{\mathbf{H}} _n = - \boldsymbol{\mathbf{D}} _2/(2m) + \boldsymbol{\mathbf{V}} _n$，其中 $ \boldsymbol{\mathbf{V}} _n$ 是对角矩阵，第 $i$ 个对角元为 $V(x_i, t_n)$。现在，就可以代入式 3 或式 4 求解了。

2. 虚时间法

预备知识 2　虚时间法求基态波函数

　　 虚时间法用于求解势阱中的基态，使用虚时间后，式 3 和式 4 分别变为

\begin{equation} \left(1+\frac12 \boldsymbol{\mathbf{H}} \Delta t \right) \boldsymbol{\mathbf{\psi}} _{n+1} = \left(1-\frac12 \boldsymbol{\mathbf{H}} \Delta t \right) \boldsymbol{\mathbf{\psi}} _n~, \end{equation}
\begin{equation} \left(\frac12 + \frac14 \boldsymbol{\mathbf{H}} \Delta t \right) \left( \boldsymbol{\mathbf{\psi}} _{n+1}+ \boldsymbol{\mathbf{\psi}} _n \right) = \boldsymbol{\mathbf{\psi}} _n~. \end{equation}

3. 代码

预备知识 3　Matlab 的稀疏矩阵

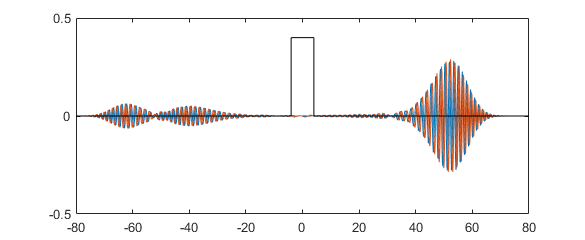
　　 Matlab 代码如下，使用式 4 ，以及 Matlab 的稀疏矩阵。势能函数可以在 V_fun 中设置，我们以方势垒为例，所有参数和 “高斯波包的方势垒散射数值计算（Matlab）” 相同。不同的是，由于我们使用迪利克雷边界条件，波函数到达边界后会发生全反射。要避免反射，可以用开放边界条件以及吸收势能。

图
图 1：运行结果

代码 1：TDSE_cn1d.m
% Crank-Nicolson 法解一维薛定谔方程
% 等间距网格，稀疏矩阵

function TDSE_cn1d
% ==== 参数设置 ======
xmin = -80; xmax = 80; Nx = 1000; % x 网格
tmin = 0; tmax = 20; Nt = 400; % 时间网格
Nplot = 10; % 画图步数
ax = [xmin, xmax, -0.5, 0.5];
% 高斯波包
x0 = -17; t0 = 0; m = 1; % 高斯波包的初始时间
p0 = 4; % 初始动量
sig_x = 2; % 初始位置， 波包宽度
% 方势垒 [-L,L], 高 V0
L = 4; V0 = 4;
V = @(x,t) V_fun(x,t,L,V0); % 势能函数
% ===================
close all;
psi_gs = @(x) 1/(2*pi*sig_x^2)^0.25/sqrt(1 + 1i*t0/(2*m*sig_x^2))...
      *exp(-(x-x0-p0*t0/m).^2/(2*sig_x)^2/(1 + 1i*t0/(2*m*sig_x^2)))...
      .*exp(1i*p0*(x-p0*t0/(2*m)));
x = linspace(xmin, xmax, Nx); dx = (xmax-xmin)/(Nx-1);
t = linspace(tmin, tmax, Nt); dt = (tmax-tmin)/(Nt-1);
psi = psi_gs(x).';
% 准备稀疏矩阵 [对角线, 上对角线, 下对角线]
ind1 = [1:Nx, 1:Nx-1, 2:Nx]; % 行标
ind2 = [1:Nx, 2:Nx, 1:Nx-1]; % 列标
% 动能矩阵非零元
T = -1/(2*m)*[-2*ones(1,Nx), ones(1,2*Nx-2)]/dx^2;
A = (1i*dt/4)*T; % 对角元稍后更新
figure; plot(x, real(psi)); hold on;
plot(x, imag(psi));
for it = 1:Nt
    % 更新对角元
    A(1:Nx) = 0.5 + (1i*dt/4)*(T(1:Nx) + V(x, t(it)+dt/2));
    Asp = sparse(ind1, ind2, A, Nx, Nx);
    tmp = Asp \ psi;
    % err = norm(Asp*tmp - psi);
    psi = tmp - psi;
    if mod(it, Nplot) == 0
        clf;
        plot(x, real(psi)); hold on;
        plot(x, imag(psi));
        plot([xmin, -L, -L, L, L, xmax], [0, 0, 0.4, 0.4, 0, 0], 'k');
        axis(ax);
        pause(0.2);
    end
end
end

% 势能函数：方势垒
function ret = V_fun(x,~,L,V0)
ret = zeros(size(x));
ret(x > -L & x < L) = V0;
end

1. ^ 参考 [1]。
2. ^ 二者是一回事，见 [1] 19.2 节。
3. ^ 或者更公平地，把式 4 中 $ \boldsymbol{\mathbf{H}} _n$ 改为 $ \boldsymbol{\mathbf{H}} _{n+1/2}$，即 $(t_n+t_{n+1})/2$ 时的哈密顿矩阵。

[1] ^ W. H. Press, et al. Numerical Recipes 3rd edition.

                     

© 小时科技 保留一切权利