高斯波包的方势垒散射数值计算(Matlab)
贡献者: addis
- 本文处于草稿阶段。
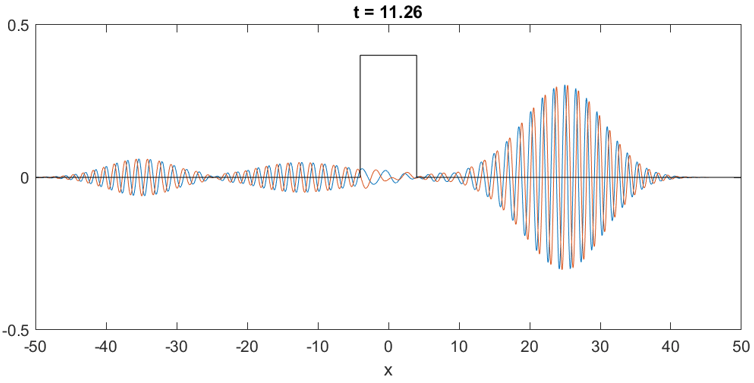
图 1:高斯波包被方势垒散射,动画见这里。蓝色和红色曲线分别是波函数的实部和虚部。注意左边反射出两个波包,它们分别来自方势垒的左侧和右侧的反射。
我们用式 8 计算波函数的含时演化。另外我们用离散的 $k_i$ 代替连续的 $k$,对 $k$ 积分改为对 $i$ 求和并乘以 $\Delta{k}$。另一种可能更常见的数值解 TDSE 算法见 “Crank-Nicolson 算法解一维含时薛定谔方程(Matlab)”。
代码中使用了 “方势垒定态波函数程序” 中的 FSB.m 和 FSB2.m。
代码 1:FSBsct.m
% 方势垒散射高斯波包
clear; close all;
% ==== 参数 ====
% 高斯波包
x0 = -17; t0 = 0; m = 1;
sig_x = 2; k0 = 4;
% 方势垒 [-L,L], 高 V0
L = 4; V0 = 4;
mode = 1; % 1: 使用类 sin,cos 基底; 2: 使用类 exp 基底
% 位置、动量、时间网格
xmin = -50; xmax = 50; Nx = 2000;
int_xmin = x0-6*sig_x; int_xmax = x0+6*sig_x;
Nk = 500; kmax = k0+4/sig_x; kmin = max(kmax/Nk, k0-4/sig_x);
tmin = 0; tmax = 20; Nt = 200;
ax = [xmin, xmax, -0.5, 0.5];
% ==============
psi = @(x) 1/(2*pi*sig_x^2)^0.25/sqrt(1 + 1i*t0/(2*m*sig_x^2))...
*exp(-(x-x0-k0*t0/m).^2/(2*sig_x)^2/(1 + 1i*t0/(2*m*sig_x^2)))...
.*exp(1i*k0*(x-k0*t0/(2*m)));
% 画 FFT 谱
x = linspace(int_xmin, int_xmax, Nx); dx = (int_xmax-int_xmin)/(Nx-1);
k = linspace(kmin, kmax, Nk); dk = (kmax-kmin)/(Nk-1);
[g1, k1] = FFT(fftresize(psi(x),Nx*2), int_xmin, dx);
g = interp1(k1, g1, k);
figure; plot(k, abs(g), '.');
axis([kmin, kmax, 0, max(abs(g))*1.1]);
xlabel k; title 'FFT of \psi(x)';
E = k.^2/(2*m);
x = linspace(xmin, xmax, Nx);
t = linspace(tmin, tmax, Nt);
figure; set(gcf, 'Unit', 'Normalized', 'Position', [0.1, 0.1, 0.4, 0.3]);
for it = 1:Nt
psi1 = zeros(size(x));
if mode == 1 % 使用类 sin,cos 基底
A = zeros(1,Nk); B = A;
for i = 1:Nk
A(i) = integral(@(x)psi(x).*FSB(x,E(i),L,m,V0,0), ...
int_xmin, int_xmax, 'RelTol', 1e-16);
B(i) = integral(@(x)psi(x).*FSB(x,E(i),L,m,V0,1), ...
int_xmin, int_xmax, 'RelTol', 1e-16);
psi1 = psi1 + dk*(A(i)*FSB(x,E(i),L,m,V0,0)...
+ B(i)*FSB(x,E(i),L,m,V0,1))*exp(-1i*E(i)*t(it));
end
else % 使用类 exp 基底
for i = 1:Nk
C1 = zeros(1,Nk); C2 = C1;
C1(i) = integral(@(x)psi(x).*conj(FSB2(x,E(i),L,m,V0,1)), ...
xmin, xmax, 'RelTol', 1e-16);
C2(i) = integral(@(x)psi(x).*conj(FSB2(x,E(i),L,m,V0,-1)), ...
xmin, xmax, 'RelTol', 1e-16);
psi1 = psi1 + dk*(C1(i)*FSB2(x,E(i),L,m,V0,1) ...
+ C2(i)*FSB2(x,E(i),L,m,V0,-1))*exp(-1i*E(i)*t(it));
end
end
clf;
plot(x, real(psi1)); hold on; plot(x, imag(psi1));
plot([xmin, -L, -L, L, L, xmax], [0, 0, 0.4, 0.4, 0, 0], 'k');
axis(ax); xlabel x; title(['t = ' num2str(t(it), '%.2f')]);
saveas(gcf, [num2str(it) '.png']);
end