一维波动方程的简单数值解(Matlab)
贡献者: addis
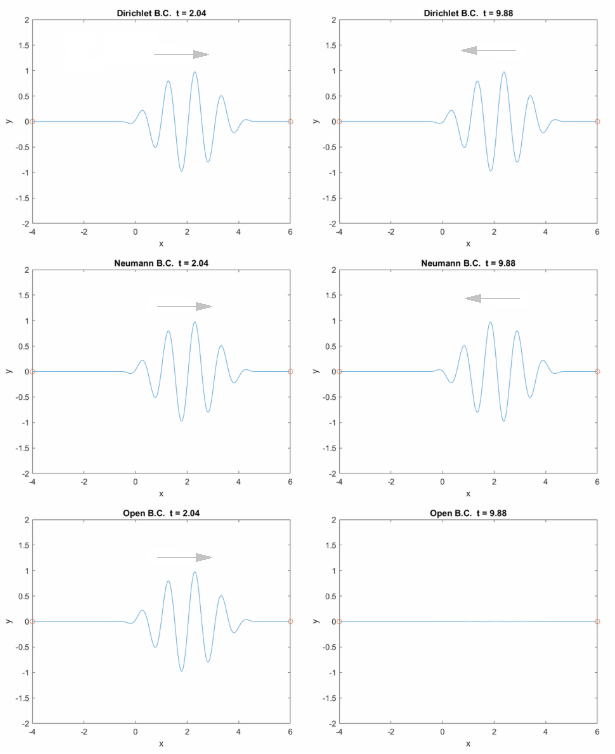
图 1:运行结果,动画见这里。Dirichlet 边界反射后发生相位反转(半波损失),Neumann 边界条件反射后无半波损失,Open 边界条件无反射。
\begin{equation}
\frac{\partial^{2}{y}}{\partial{x}^{2}} - \frac{1}{c^2} \frac{\partial^{2}{y}}{\partial{t}^{2}} = 0~.
\end{equation}
其中 $y(x, t)$ 是坐标和时间的函数。这里介绍一个简单的有限差分(finite difference)法,即把空间 $x$ 和时间 $t$ 划分成等距离的网格 $x_1, \dots, x_{Nx}$ 和 $t_1, \dots, t_{Nt}$,步长分别为 $\Delta x$ 和 $\Delta t$。我们将每个格点处的函数值记为 $y_{i,n} = y(x_i, t_n)$
有了网格以后,我们可以用有限差分表示二阶导数(式 5 )得
\begin{equation}
\frac{y_{i-1,n} - 2y_{i,n} + y_{i+1,n}}{\Delta x^2} - \frac{1}{c^2} \frac{y_{i, n-1} - 2y_{i, n} + y_{i, n+1}}{\Delta t^2} = 0~.
\end{equation}
\begin{equation}
y_{i, n+1} = 2y_{i, n} - y_{i, n-1} + C^2(y_{i-1,n} - 2y_{i,n} + y_{i+1,n})~.
\end{equation}
\begin{equation}
C = c \frac{\Delta t}{\Delta x}~
\end{equation}
1. 边界条件
如果令网格边界处 $y = 0$(Dirichlet 边界条件)则会发生全反射且有半波损失。若边界处使用 $ \partial y/\partial x = 0$(Neumann 边界条件)同样会发生全反射但没有半波损失。
另外有一种很有用的边界条件叫 open boundary condition 或者 radiation boundary condition2,可以使波动完全不发生反射
\begin{equation}
\frac{\partial y}{\partial t} + c \frac{\partial y}{\partial x} = 0~.
\end{equation}
2. Matlab 程序
程序如下,运行结果见图 1 。
代码 1:wave1D.m
% 一维波动方程数值解
% 参考 https://wuli.wiki/online/W1dNum.html
function wave1D
close all;
% ==== 参数 ====
c = 1; % 波速
xmin = -4; xmax = 6; Nx = 1200; % 空间格点
tmin = 0; tmax = 12; Nt = 2401; % 时间格点
k = 6; Ncyc = 5; % 初始波包的波数和周期数
bc = 'd'; % 边界条件: [d] Dirichlet, [n] Neumann, [o] Open
% ================
x = linspace(xmin, xmax, Nx)';
t = linspace(tmin, tmax, Nt);
dx = (xmax - xmin)/(Nx - 1);
dt = (tmax - tmin)/(Nt - 1);
C = c*dt/dx; C2 = C*C;
y = zeros(Nx, Nt);
y(:,1) = y0(x, k, Ncyc);
y(:,2) = y0(x - c*dt, k, Ncyc);
% 二阶差分(边界元设为 0)
D2 = @(v) [0;
v(1:end-2) - 2*v(2:end-1) + v(3:end);
0];
figure;
for n = 2:Nt - 1
y(:,n+1) = 2*y(:,n) - y(:,n-1) + C2*D2(y(:,n));
y = bc_set(y, n+1, bc, c, dx, dt);
if (mod(n, 8) == 0)
clf; plot(x, y(:,n+1)); axis([xmin,xmax,-2,2]);
hold on; scatter([xmin,xmax], [y(1,n+1), y(end,n+1)]);
if bc == 'd'
title(['Dirichlet B.C. t = ', num2str(t(n+1), '%.2f')]);
elseif bc == 'n'
title(['Neumann B.C. t = ', num2str(t(n+1), '%.2f')]);
else
title(['Open B.C. t = ', num2str(t(n+1), '%.2f')]);
end
xlabel x; ylabel y;
drawnow;
% saveas(gcf, [bc 'wv' num2str(n) '.png']); % 保存图片文件
end
end
end
% 初始波包
% sin^2 波形
function y = y0(x, k, Ncyc)
T = 2*pi/k;
L = T*Ncyc/2;
y = zeros(size(x));
k0 = k / Ncyc / 2;
for i = 1:numel(x)
xx = x(i);
if abs(xx) <= L
y(i) = cos(k0*xx)^2 * sin(k*xx);
end
end
end
% 处理边界值
function y = bc_set(y, n, bc, c, dx, dt)
if bc == 'd' % Dirichlet
y(1, n) = 0;
y(end, n) = 0;
elseif bc == 'n' % Neumann
y(1, n) = y(2, n);
y(end, n) = y(end-1, n);
elseif bc == 'o' % Open
y(end, n) = y(end-1, n) - 1/c * (y(end-1, n) - y(end-1, n-1))*dx/dt;
end
end