有限深方势阱束缚态程序(Matlab)
贡献者: addis
以下给出求解束缚态的 Matlab 代码。算法用二分法解图 2 和图 3 即可,这可以确保找到所有解。
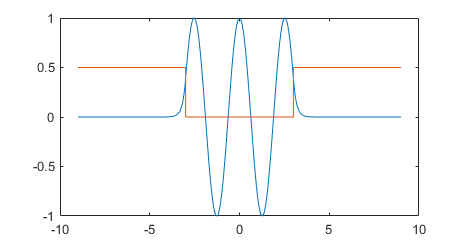
图 1:运行结果:第四激发态
代码 1:FSW_bound_eng.m
% 计算有限深势阱的束缚态参数 k, ka
% 区间 [-L/2,L/2], 内部势能 -V0
% 能级为 E = k.^2/2 - V0
% k 按小到大排序
% 波函数依次是偶函数、奇函数、偶函数…
function [k, ka] = FSW_bound_eng(L, V0, m)
if V0 <= 0
error('V0 > 0');
end
% 奇波函数
z0 = L*sqrt(2*m*V0)/2;
N = floor(z0/pi + 0.5); % 解的个数
k1 = zeros(1,N);
fun = @(z)-cot(z) - sqrt((z0/z)^2 - 1);
for i = 1:N-1
k1(i) = (2/L)*fzero(fun, [(i-0.5)*pi, i*pi-eps]);
end
if N > 0
k1(N) = (2/L)*...
fzero(fun, [(N-0.5)*pi, min(N*pi-eps, z0)]);
end
% 偶波函数
N = floor(z0/pi) + 1; % 解的个数
k2 = zeros(1,N);
fun = @(z)tan(z) - sqrt((z0/z)^2 - 1);
for i = 0:N-2
k2(i+1) = (2/L)*fzero(fun, [i*pi+eps, (i+0.5)*pi-eps]);
end
k2(N) = (2/L)*...
fzero(fun, [(N-1)*pi+eps, min((N-0.5)*pi-eps, z0)]);
k = sort([k1, k2]);
ka = sqrt(2*m*V0 - k.^2);
end
代码 2:FSW_bound_psi.m
% 已知方势阱束缚态波函数的参数, 求波函数 psi(x)
% 已知 k, ka, L, isodd (奇偶性)
function psi = FSW_bound_psi(L, k, ka, isodd, x)
mark = abs(x) <= L/2;
markL = x < -L/2; markR = x > L/2;
psi = zeros(1, numel(x));
if isodd % 奇函数
D = sin(k*L/2)/exp(-ka*L/2);
psi(mark) = sin(k*x(mark));
psi(markL) = -D*exp(ka*x(markL));
else % 偶函数
D = cos(k*L/2)/exp(-ka*L/2);
psi(mark) = cos(k*x(mark));
psi(markL) = D*exp(ka*x(markL));
end
psi(markR) = D*exp(-ka*x(markR));
end
代码 3:FSW_bound_plt.m
% 有限深方势阱的波函数画图演示
% === 参数设置 ===
L = 6; V0 = 20; m = 1;
xmin = -1.5*L; xmax = 1.5*L; Nx = 1000;
% ================
[k, ka] = FSW_bound_eng(L,V0,m);
N = numel(ka);
x = linspace(xmin, xmax, Nx);
for n = 1:N
isodd = mod(n+1,2); % n=1 是偶函数
psi = FSW_bound_psi(L, k(n), ka(n), isodd, x);
figure; plot(x, psi); hold on;
plot([xmin,-L/2,-L/2,L/2,L/2,xmax],...
[1,1,0,0,1,1]*0.5); % 画势阱
end