贡献者: Siegfried; 欄、停敘; addis
极坐标系中,我们可以用一元函数
\begin{equation}
r = f(\theta)~
\end{equation}
表示一条曲线。简单的例子如
阿基米德螺线或
圆锥曲线。以下我们讨论如何从函数中计算曲线的一些特征。
1. 计算某点切线的方向
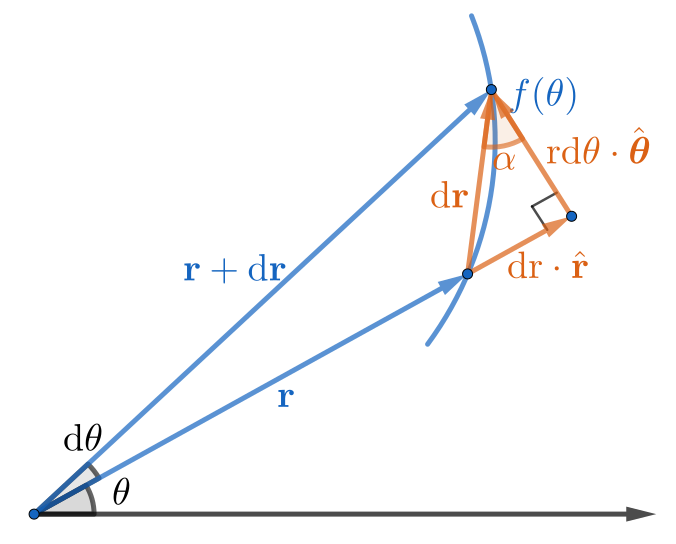
在 $x$-$y$ 平面直角坐标系中,我们可以通过求导($ \mathrm{d}{y}/\mathrm{d}{x} $)计算曲线某点切线,那么式 1 表示的极坐标中如何求某点切线的方向呢?可以证明,切线与 $ \hat{\boldsymbol{\mathbf{\theta}}} $ 方向的夹角为
\begin{equation}
\tan\alpha = \frac{1}{r} \frac{\mathrm{d}{r}}{\mathrm{d}{\theta}} = \frac{f'(\theta)}{f(\theta)}~,
\end{equation}
或者说与 $ \hat{\boldsymbol{\mathbf{r}}} $ 方向的夹角为 $\pi/2 - \alpha$。
图 1:极坐标切线示例
证明:
对极坐标中的位置矢量 $ \boldsymbol{\mathbf{r}} = r \hat{\boldsymbol{\mathbf{r}}} $ 两边取全微分,得到:
\begin{equation}
\,\mathrm{d}{ \boldsymbol{\mathbf{r}} } = \,\mathrm{d}{r} \hat{\boldsymbol{\mathbf{r}}} + r \,\mathrm{d}{ \hat{\boldsymbol{\mathbf{r}}} } ~.
\end{equation}
由于:
\begin{equation}
\,\mathrm{d}{ \hat{\boldsymbol{\mathbf{r}}} } = \frac{\partial \hat{\boldsymbol{\mathbf{r}}} }{\partial r} \,\mathrm{d}{r} + \frac{\partial \hat{\boldsymbol{\mathbf{r}}} }{\partial \theta} \,\mathrm{d}{\theta} ~.
\end{equation}
其中,$ \frac{\partial \hat{\boldsymbol{\mathbf{r}}} }{\partial r} $ 和 $ \frac{\partial \hat{\boldsymbol{\mathbf{r}}} }{\partial \theta} $ 可由极坐标系中单位矢量的偏导处证得,结果带入式 4 ,得到:
\begin{equation}
\,\mathrm{d}{ \boldsymbol{\mathbf{r}} } = \,\mathrm{d}{r} \hat{\boldsymbol{\mathbf{r}}} + r \,\mathrm{d}{\theta} \hat{\boldsymbol{\mathbf{\theta}}} ~.
\end{equation}
上式中,$ \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } $ 的方向,即是切线的方向。切线与 $ \hat{\boldsymbol{\mathbf{\theta}}} $ 方向的夹角为:
\begin{equation}
\tan \alpha = \frac{\partial \boldsymbol{\mathbf{r}} }{\partial \hat{\boldsymbol{\mathbf{r}}} } \left/ \frac{\partial \boldsymbol{\mathbf{r}} }{\partial \hat{\boldsymbol{\mathbf{\theta}}} } \right.
=\frac{1}{r} \frac{\mathrm{d}{r}}{\mathrm{d}{\theta}} = \frac{f'(\theta)}{f(\theta)}~.
\end{equation}
2. 曲线长度
若用 $\theta \in [\theta_1, \theta_2]$,来表示曲线的一段,那么其长度为
\begin{equation}
l = \int_{\theta_1}^{\theta_2} \sqrt{f(\theta)^2 + f'(\theta)^2} \,\mathrm{d}{\theta} ~.
\end{equation}
证明:继式 5 ,
\begin{equation}
\begin{split}
\,\mathrm{d}{l} = | \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } | &= \sqrt{( \,\mathrm{d}{r} )^2 + (r \,\mathrm{d}{\theta} )^2} \\
&= \sqrt{\left( \frac{\mathrm{d}{r}}{\mathrm{d}{\theta}} \right)^2 + r^2} \,\mathrm{d}{\theta} \\
&= \sqrt{f(\theta)^2 + f'(\theta)^2} \,\mathrm{d}{\theta} ~.
\end{split}
\end{equation}
对区间 $[\theta_1,\theta_2]$ 积分后,即可求得该段曲线的长度,即式 7 。
3. 直线的极坐标方程
设极坐标为 $(\rho,\theta)$,过点 $(a,0)$,且与极轴夹角为 $\alpha$ 的直线极坐标方程为:
\begin{equation}
\rho \sin\left(\alpha-\theta\right) =a\sin\alpha~.
\end{equation}
通过调整变形,可以讨论不同情况下的特殊形式:
1. 直线过极点
此时 $a=0$,代入式 9 可知,此时表达式为:
\begin{equation}
\theta=\alpha~.
\end{equation}
2.与极轴垂直,极点到直线距离为 $|a|$。
此时 $\displaystyle\alpha={\pi\over2}$,代入式 9 可知,此时表达式为:
\begin{equation}
\rho\cos\theta=a~.
\end{equation}
若 $a>0$ 则直线在极点右侧,否则直线在极点左侧。
3.与极轴平行,极点到直线距离为 $|a|$。
此时由于直线不再过点 $(a,0)$,于是不能直接代入得到表达式。根据此时直线表达式为 $y=a$,而极坐标中 $y=\rho\sin\theta$,可知,此时表达式为:
\begin{equation}
\rho\sin\theta=a~.
\end{equation}
若 $a>0$ 则直线在极点上侧,否则直线在极点下侧。