贡献者: addis; jiangnan
1. 二维分布函数
我们以打靶为例来引入二元概率分布函数,以及在直角坐标系和极坐标系中如何分析各种平均值。我们在靶上建立 $x$-$y$ 直角坐标系,类比一维概率分布函数的定义,二维概率分布可以用一个二元函数表示为 $f(x, y)$,也叫概率密度(probability density)。子弹落在一个长方形区域内(令 $x \in [x_1, x_2]$,$y \in [y_1, y_2]$)的概率可以用二重积分表示
\begin{equation}
P = \int_{y_1}^{y_2} \int_{x_1}^{x_2} f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~.
\end{equation}
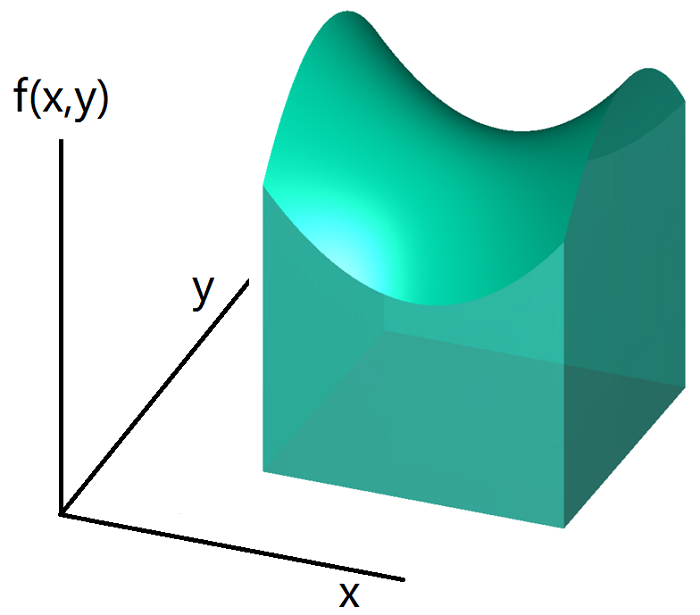
从几何上理解,$f(x, y)$ 可以看作一张三维空间中的曲面,而这个二重积分则表示曲面和 $x$-$y$ 平面之间的一个体积(
图 1 )。
图 1:$f(x, y)$ 曲面下的体积
类比一维情况,概率归一化条件为
\begin{equation}
\int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} = 1~.
\end{equation}
由于概率的量纲是 1,$f(x, y)$ 的国际单位量纲就是 $ \,\mathrm{m^{-2}} $,即面积的倒数。
2. 平均值
类比式 10 ,离散情况下,令 $P_i$ 是 $(x_i, y_i)$ 出现的概率,函数 $g(x,y)$ 的平均值为
\begin{equation}
\left\langle g \right\rangle = \sum_{i=1}^N g(x_i, y_i) P_i~.
\end{equation}
拓展到连续的情况,类比
式 11 ,$g(x, y)$ 的平均值可以定义为
\begin{equation}
\left\langle g \right\rangle = \int_{-\infty}^{+\infty} \int_{-\infty}^{+\infty} g(x, y) f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~.
\end{equation}
例如位置矢量的 $x$ 和 $y$ 分量平均值分别为
\begin{equation}
\left\langle x \right\rangle = \iint x f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~,
\end{equation}
\begin{equation}
\left\langle y \right\rangle = \iint y f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~.
\end{equation}
以上两式也可以用位置矢量 $ \boldsymbol{\mathbf{r}} $ 表示为(这时 $ \boldsymbol{\mathbf{g}} $ 的函数值是矢量)
\begin{equation}
\left\langle \boldsymbol{\mathbf{r}} \right\rangle = \iint \boldsymbol{\mathbf{r}} f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~,
\end{equation}
点 $(x,y)$ 到原点距离的距离 $r$ 的平均值
\begin{equation}
\left\langle r \right\rangle = \iint \sqrt{x^2 + y^2} f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~.
\end{equation}
注意区分该式和
式 7 式的意义,平均位置和平均距离是两个不同的概念:如果 $f(x, y)$ 是关于原点中心对称的函数,则平均位置为 $(0, 0)$,而平均距离不为零。
距离平方 $r^2$ 的平均值
\begin{equation}
\left\langle r^2 \right\rangle = \iint (x^2 + y^2) f(x, y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~.
\end{equation}
3. 概率分布的极坐标表示
除了直角坐标系外,我们也可以使用极坐标表示分布函数,记为1 $f(r, \theta)$,那么概率归一化条件变为
\begin{equation}
\int_0^\infty \int_{0}^{2\pi} f(r, \theta)\,\, r \,\mathrm{d}{\theta} \,\mathrm{d}{r} = 1~,
\end{equation}
函数 $g(r, \theta)$ 的平均值变为
\begin{equation}
\left\langle g \right\rangle = \int_0^\infty \int_{0}^{2\pi} g(r, \theta) f(r, \theta)\,\, r \,\mathrm{d}{\theta} \,\mathrm{d}{r} ~.
\end{equation}
例如
式 9 变为
\begin{equation}
\left\langle r^2 \right\rangle = \int_0^\infty \int_{0}^{2\pi} r^2 f(r, \theta)\,\, r \,\mathrm{d}{\theta} \,\mathrm{d}{r}
= \int_0^\infty \int_{0}^{2\pi} r^3 f(r, \theta) \,\mathrm{d}{\theta} \,\mathrm{d}{r} ~.
\end{equation}
4. 圆对称分布
继续打靶的例子,我们接下来讨论圆对称的概率分布(在三维情况下叫做球对称),即 $f(r, \theta)$ 的值只和 $r$ 有关而与 $\theta$ 无关的情况。为了书写方便可记 $f(r) \equiv f(r, \theta)$。归一化条件式 10 化简为(先完成关于 $\theta$ 积分得 $2\pi$)
\begin{equation}
2\pi \int_0^\infty r f(r) \,\mathrm{d}{r} = 1~.
\end{equation}
一个容易混淆的概念是,$f(r)$ 并不是变量 $r$ 的概率分布函数。也就是说 $\int_a^b f(r) \,\mathrm{d}{r} $ 并不是子弹落在圆环 $r \in [a, b]$ 内的概率。若将 $r$ 的概率分布函数记为 $F(r)$,子弹落在圆环中的概率应该是
\begin{equation}
P_{ab} = \int_a^b F(r) \,\mathrm{d}{r} = \int_a^b 2\pi r f(r) \,\mathrm{d}{r} ~.
\end{equation}
由于两个定积分在任何区间都相等,两个被积函数必须相等,即
\begin{equation}
F(r) = 2\pi r f(r)~.
\end{equation}
这时以上的平均值也可以得到进一步化简,例如
式 12 变为
\begin{equation}
\left\langle r^2 \right\rangle = \int_0^\infty r^2 F(r) \,\mathrm{d}{r}
= 2\pi \int_0^\infty r^3 f(r) \,\mathrm{d}{r} ~.
\end{equation}
5. 多随机变量的函数的分布
我们在前面已经知道定义在随机变量 X、Y 上的函数 $g(x,y)$ 的平均值 $\bar{g}$ 如何计算,但实际上如果关注每次 $g(x,y)$ 的值,我们会发现 $g(x,y)$ 也满足一定的概率分布,那如何求解这个概率分布呢?我们以二元随机变量的几个例子为例说明。首先我们引入分布函数这个概念
定义 1 分布函数与边缘分布函数
对于一个随机变量 X,我们定义分布函数为 $F(\alpha)=P(x\leq \alpha) = \int_{-\infty}^{\alpha} f(x)dx$。对于一个二维连续随机变量(X,Y),其边缘分布函数有两个,X 的边缘分布函数 $F_X(x)$ 与 Y 的边缘分布函数 $F_Y(y)$,定义为
\begin{align}
F_X(x) = \int_{-\infty}^{+\infty} dy^\prime \int_{-\infty}^{x} dx^\prime f(x^\prime,y^\prime)\\~
F_Y(y) = \int_{-\infty}^{+\infty} dx^\prime \int_{-\infty}^y dy^\prime f(x^\prime,y^\prime)~
\end{align}
类似地我们可以定义边缘概率密度函数 $f_X(x) = \frac{dF_X(x)}{dx}$,$f_Y(y) = \frac{dF_Y(y)}{dy}$。
例 1
我们定义随机变量 $Z=X+Y$,求 $Z$ 的分布的概率密度函数,这时我们要先去求 $Z$ 的分布函数,$F_Z(\alpha)=P(z\leq \alpha) = P(x+y\leq \alpha)$,而 $P(x+y\leq \alpha) = \int_{-\infty}^{+\infty}dx \int_{-\infty}^{\alpha-x} dy f(x,y)$,当给定二元分布函数的概率密度 $f(x,y)$ 后,$F_Z(\alpha)$ 即可积分算出。继而通过 $f_Z(z) = \frac{d F_Z(z)}{dz}$ 即可求得。
1. ^ 在数学上,该式两边是两个不同的二元函数,应该使用不同的函数名如 $g(r, \theta) = f(x, y)$,但在一些物理教材中,我们有时为了方便不区分函数名,直接把 $g(r, \theta)$ 写成 $f(r, \theta)$。