贡献者: addis
1. 面积分
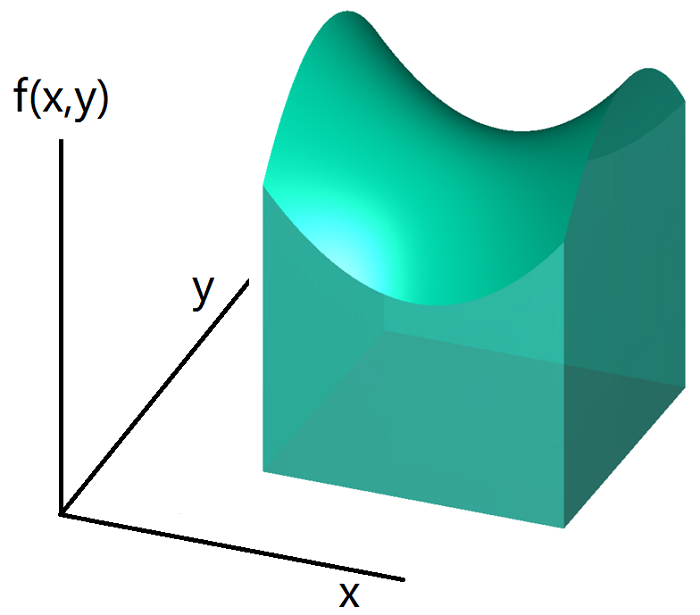
面积分也叫二重积分,可以看做一元函数定积分的一种拓展。从几何上来理解,如果一元函数的定积分是计算一定区间内被积函数曲线与坐标轴之间的面积,那么二重积分就是计算一定二维区域内被积函数曲面与坐标轴平面之间的体积(式 1 )。
图 1:$f(x, y)$ 曲面下的体积
对一元函数的定积分,我们需要指定积分的下限和上限,那么对于面积分,我们需要指定 $x$-$y$ 平面上的一块定积分的区域 $\mathcal S$。例如式 1 表示的面积分的区域就是一个正方形。与一元函数的情况相同,我们把积分区域划分成许多小长方形,每个小长方形的面积为 $\Delta x_i \Delta y_j$。把二重积分对应的体积用一个个柱体来近似,每个柱体的体积为 $\Delta x_i \Delta y_j f(x_i, y_i)$ 其中 $(x_i, y_i)$ 是长方形中任意一点。当这些小长方形趋近无穷小时,就得到了精确的体积。用双重极限表示为
\begin{equation}
V = \lim_{\substack{\Delta x_i\to 0\\ \Delta y_j\to 0}} \sum_{i, j} f(x_i,y_j) \Delta x_i \Delta y_j~.
\end{equation}
用积分符号可以把上式简记为
\begin{equation}
V = \iint_{\mathcal{S}} f(x,y) \,\mathrm{d}{x} \,\mathrm{d}{y} ~,
\end{equation}
注意积分区域 $\mathcal S$ 可以是任何形状的。我们通过一个例子来说明具体如何计算面积分
例 1 抛物线下的体积
二元函数 $f(x,y) = x^2 + y^2$,可以在直角坐标系 $xyz$ 代表一个抛物面。现在我们指定一个二维区域,是由 $y_1(x) = -x$,$y_2(x) = x$ 以及 $x = 1$ 所围成的三角形。现在我们以这个三角形为底取一个无限高的三棱柱,求三棱柱被 $f(x,y)$ 截去的有限部分的体积 $V$。
那如何计算这个积分呢?我们可以先计算任意 $x$ 处的横截面积 $S(x)$。这个横截面与曲面相交的曲线方程为 $f(x,y)$(把 $x$ 看做常数,$y$ 看做变量),横截面积为
\begin{equation}
S(x) = \int_{y_1(x)}^{y_2(x)} f(x,y) \,\mathrm{d}{y} = \frac13 [y_2^3(x) - y_1^3(x)] + x^2[y_2(x) - y_1(x)] = \frac83 x^3~.
\end{equation}
现在根据一元函数定积分的定义,体积等于横截面积 $S(x)$ 在 $x$ 方向的定积分
\begin{equation}
V = \lim_{\Delta x_i\to 0} \sum_{i} S(x_i) \Delta x_i = \int_0^1 S(x) \,\mathrm{d}{x} = \frac23 (1^4 -0^4) = \frac23~.
\end{equation}
要从定义上证明这种方法可行,我们可以把
式 1 写成
\begin{equation}
V = \lim_{\Delta x_i\to 0} \sum_{i} \left[\lim_{\Delta y_j\to 0}\sum_{j} f(x_i,y_j) \Delta y_j \right] \Delta x_i~.
\end{equation}
可见中括号内的极限就是定积分
式 3 ,外面的极限就是定积分
式 4 。把上式记为一条积分式就是
\begin{equation}
V = \int_0^1 \left[\int_{y_1(x)}^{y_2(x)} f(x,y) \,\mathrm{d}{y} \right] \,\mathrm{d}{x} ~.
\end{equation}
另一种等效的书写方法是,把 $\int \,\mathrm{d}{x} , \int \,\mathrm{d}{y} $ 看成像 $ \mathrm{d}/\mathrm{d}{x} , \mathrm{d}/\mathrm{d}{y} $ 一样的整体算符,写在被积函数前面,使公式看起来更为简洁
\begin{equation}
V = \int_0^1 \,\mathrm{d}{x} \int_{y_1(x)}^{y_2(x)} \,\mathrm{d}{y} f(x,y)~.
\end{equation}
总结起来,要在直角坐标系中计算二重积分,就先选取一个变量 $y$(也可以是 $x$)进行定积分,积分的上下限分别是二重积分区域 $\mathcal{S}$ 的两条边界线 $y_1(x)$ 和 $y_2(x)$。积分的结果中只含有 $x$,这时再对 $x$ 进行定积分即可。
2. 体积分
体积分也叫三重积分,类比面积分不难理解其概念
例 2 不均匀物体的质量
一个几何体由 $x = 0, y = 0, z = 0$ 三个平面和 $x + y + z = 1$ 平面包围而成,其密度为 $f(x,y,z) = x + y + z$,求几何体的总质量 $M$。
用定积分的思想,我们可以延三个方向把几何体划分成许多小块 $(i,j,k)$,每个小块的长宽高分别为 $\Delta x_i, \Delta y_j, \Delta z_k$。$x_i, y_j, z_k$ 分别为区间 $\Delta x_i, \Delta y_j, \Delta z_k$ 中的任意一点。物体的总质量可以用极限表示为
\begin{equation}
V = \lim_{\substack{\Delta x_i\to 0\\ \Delta y_j\to 0\\ \Delta z_k\to 0}} \sum_{i, j, k} f(x_i,y_j,z_k) \Delta x_i \Delta y_j \Delta z_k~.
\end{equation}
用三重积分可以把这个
三重极限表示为
\begin{equation}
V = \iiint_{\mathcal{V}} f(x,y,z) \,\mathrm{d}{x} \,\mathrm{d}{y} \,\mathrm{d}{z} ~,
\end{equation}
其中 $\mathcal{V}$ 表示几何体所占的空间。我们先把密度函数 $f(x,y,z)$ 沿 $z$ 方向积分得到 “面密度” $\sigma(x,y)$(可以想象把几何体在 $z$ 方向压成一个薄板后所具有的面密度关于 $x,y$ 的函数),积分上下限分别为 $z_2(x,y) = 1 -x - y$ 和 $z_1(x,y) = 0$
\begin{equation} \begin{aligned}
\sigma(x,y) &= \int_{0}^{1-x-y} (x+y+z) \,\mathrm{d}{z} \\
&= (x + y)[z_2(x,y) - z_1(x,y)] + \frac12 [z_2^2(x,y) - z_1^2(x,y)]\\
&= (x + y)(1-x-y) + \frac12 (1-x-y)^2\\
&= \frac12 (1 - x^2 - y^2) - xy~.
\end{aligned} \end{equation}
再沿 $y$ 方向积分得到 “线密度” $\lambda(x)$(可以想象把薄板沿 $y$ 方向压缩成一条线后所具有的线密度关于 $x$ 的函数),积分的上下限分别为 $y_2(x) = 1-x$ 和 $y_1(x) = 0$
\begin{equation} \begin{aligned}
\lambda(x) &= \int_{0}^{1-x} \sigma(x,y) \,\mathrm{d}{y} \\
&= \frac12 (1-x^2) (1-x) - \frac16 (1-x)^3 - \frac12 x(1-x)^2\\
&= \frac{x^3}{6} - \frac{x}{2} + \frac13~,
\end{aligned} \end{equation}
最后把线密度从 $1$ 和 $0$ 积分得到总质量
\begin{equation} \begin{aligned}
M &= \int_{0}^{1} \lambda(x) \,\mathrm{d}{x} = \left[\frac{1}{24} x^4 - \frac14 x^2 + \frac13 x \right] _0^1 = \frac18~.
\end{aligned} \end{equation}
与二重积分类似,要从定义上来证明这种算法可行,就把
式 8 改写成
\begin{equation}
M = \lim_{\Delta x_i\to 0} \sum_{i} \left[\lim_{\Delta y_j\to 0}\sum_{j} \left(\lim_{\Delta z_k\to 0} \sum_{k} f(x_i,y_j,z_k) \Delta z_k \right) \Delta y_j \right] \Delta x_i~.
\end{equation}
可见从内到外的三个极限分别为三个变量的一元定积分,即
\begin{equation}
M = \int_{0}^{1} \,\mathrm{d}{x} \int_{0}^{1-x} \,\mathrm{d}{y} \int_{0}^{1-x-y} \,\mathrm{d}{z} f(x,y,z)~.
\end{equation}
在柱坐标和球坐标下,函数 $f(x,y,z)$ 变为 $f(r,\theta,z)$ 和 $f(r,\theta,\phi)$,而体积元 $ \,\mathrm{d}{x} \,\mathrm{d}{y} \,\mathrm{d}{z} $ 变为 $r \,\mathrm{d}{r} \,\mathrm{d}{\theta} \,\mathrm{d}{z} $ 式 8 和 $r^2\sin\theta \,\mathrm{d}{r} \,\mathrm{d}{\theta} \,\mathrm{d}{\phi} $ 式 9 .故三重积分式 9 在柱坐标和球坐标下分别表示为
\begin{equation}
\iiint_{\mathcal{V}}f(r,\theta,z)r \,\mathrm{d}{r} \,\mathrm{d}{\theta} \,\mathrm{d}{z} \quad \&\quad
\iiint_{\mathcal{V}}f(r,\theta,\phi)r^2\sin\theta \,\mathrm{d}{r} \,\mathrm{d}{\theta} \,\mathrm{d}{\phi} ~.
\end{equation}
未完成:链接一下柱坐标,球坐标系中的面积分