静电场（高中）

贡献者： kahoyip

1. 电荷

　　经摩擦的物体能吸引轻小的物体，我们就说它带有电荷。电荷分为正电荷和负电荷，用毛皮摩擦过的橡胶棒带负电荷，用丝绸摩擦过的玻璃棒带正电荷。

　　电荷间的相互作用规律：同种电荷相互排斥，异种电荷相互吸引。

电荷量

　　电荷量表示电荷的多少。电荷量的单位是库仑（简称库），符号为 $\mathrm{C}$。

　　正电荷的电荷量为正值（“$+$” 号通常会省略），负电荷的电荷量为负值，要注意这里的正、负表示电荷种类，比较电荷量的多少要看电荷量的绝对值。

元电荷

　　又称基本电荷，是一个电子或一个质子所带电荷量的绝对值，用字母 $e$ 表示，$e = 1.602176634 \times 10^{-19} \mathrm{C}$¹，近似计算时取 $e = 1.60 \times 10^{-19} \mathrm{C}$。任何带电体所带的电荷量都是元电荷的整数倍。

点电荷

　　带电体之间的距离比带电体自身大小大得多时，带电体自身的大小、形状、电荷分布对带电体之间作用力的影响可忽略不计，这时可把带电体看成带电的点，称为点电荷。点电荷是一种理想化模型。

比荷

　　带电体所带电量与其质量之比，叫做比荷，单位为库仑每千克（$\mathrm{C/kg}$）。

　　电子的质量 $m_e \approx 9.11 \times 10^{-31} \mathrm{kg}$，则电子的比荷

\begin{equation} \frac{e}{m_e} \approx 1.76 \times 10^{11} \,\mathrm{C/kg}~. \end{equation}

场源电荷

　　研究电场问题时，把产生电场的电荷称为场源电荷。

试探电荷

　　用于放入电场中研究电场性质的电荷叫做试探电荷（或检验电荷）。试探电荷的带电量和体积都要求足够小，从而可忽略其对原电场的影响，以及便于研究电场中各点的性质。

2. 起电方式

摩擦起电

　　用摩擦的方法使两个由不同物质组成的物体带电的现象，叫做摩擦起电。摩擦起电的实质是电子的转移，在两物体相互摩擦时，电子从束缚电子能力弱的物体转移到束缚电子能力强的物体，摩擦后两物体带等量异种电荷。

感应起电

　　一个带电的物体和一个不带电的导体相互靠近时，由于电荷之间的相互作用，导体靠近带电体的一端带异种电荷，远离带电体的一端则带同种电荷，这种现象叫做静电感应。静电感应的实质是导体内部电子的转移。利用静电感应时物体带电的方法叫做感应起电。

接触起电

　　让不带电的物体与带电体相互接触，使不带电的物体带上与带电体同种的电荷，这种起电方式叫做接触起电。接触起电的实质是电子在两接触物体之间的转移。

3. 电荷守恒定律

　　电荷既不能被创造，也不能被消灭，只能从一个物体转移到另一个物体，或者从物体的一部分转移到另一部分。在转移过程中，电荷的总量保持不变。

4. 库仑定律

　　真空中两个静止的点电荷之间的相互作用力，叫做静电力（或库仑力），其大小与两个点电荷的电荷量（分别为 $q_1$ 和 $q_2$）的乘积成正比，与两个点电荷之间距离（$r$）的二次方成反比：

\begin{equation} F=k \frac{q_1 q_2}{r^2}~. \end{equation}

　　库仑力的方向在两点电荷的连线上，可利用 “同种电荷相互排斥，异种电荷相互吸引” 来判断。

　　注意，与万有引力定律（子节 2 ）类似，当两个带电体之间的距离 $r$ 趋于 $0$ 时，它们不能被看作点电荷，上式不再适用，无法得出静电力趋于无穷大的结论。

静电力常量

　　式 2 的 $k$ 叫静电力常量（或库仑常数）。

\begin{equation} k = \frac{1}{4\pi\epsilon_0} \approx 9.0 \times 10^{9} \,\mathrm{N m^2/C^2}~. \end{equation}

　　 $\epsilon_0$ 是真空介电常数（或真空电容率），$\epsilon_0 \approx 8.85 \times 10^{-12} \,\mathrm{C^2/(N \cdot m^2)}~. $

5. 电场

　　电荷周围存在由它产生的电场，电荷之间的相互作用是通过电场的作用产生的。由静止电荷产生的电场叫做静电场。

电场强度

　　试探电荷在电场中某一位置受到静电力 $ \boldsymbol{\mathbf{F}} $ 与它的电荷量 $q$ 之比，叫做电场强度，简称场强，用 $ \boldsymbol{\mathbf{E}} $ 表示，单位是牛每库（$\mathrm{N/C}$）或伏每米（$\mathrm{V/m}$），其大小为

\begin{equation} E =\frac {F}{q}~. \end{equation}

　　电场强度是一个矢量，某一点的场强方向与正电荷在该点所受静电力的方向相同，与负电荷在该点所受的静电力方向相反。

　　若电场中各点的场强大小和方向都相同，则这个电场叫匀强电场。

点电荷的电场

　　电荷量为 $Q$ 的场源电荷在真空中静止，根据式 2 和式 4 可得，该场源电荷在与其距离为 $r$ 处的场强大小为

\begin{equation} E=k\frac{Q}{r^2}~. \end{equation}

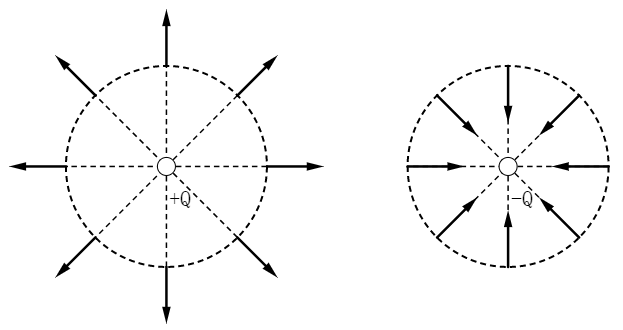
　　以场源电荷为球心，在任意一球面上各点的场强大小相等。如图 1 所示，若场源电荷为正电荷，其场强方向沿半径指向外部；若场源电荷为负电荷，其场强方向沿半径指向球心。

图 1：点电荷的电场

　　若场源电荷为多个点电荷，则电场中某一点的场强等于各点电荷单独在此处产生的场强的矢量和。

电场线

　　在电场画出一系列有方向的曲线，曲线上每一点的切线方向都跟该点的电场强度方向一致，这样的曲线叫做电场线。电场线分布的疏密程度反映了电场的强弱，电场线分布密的位置电场强度大，电场线分布疏的位置电场强度小。

　　电场线是为了形象地描述电场而引入的，是假想的，并不客观存在。

6. 静电力做功

预备知识　功和机械能

　　与重力做功类似，电荷在电场中运动时，静电力对电荷做的功只与电荷的初末位置有关，而与电荷的运动路径无关。

　　在场强为 $ \boldsymbol{\mathbf{E}} $ 的匀强电场中，若电荷沿电场线方向运动的距离为 $d$，则静电力做功为

\begin{equation} W=qEd~. \end{equation}

　　对于非匀强电场的静电力做功，可考虑用动能定理（式 7 ）、电势能（式 7 ）或电势差（式 10 ）等进行求解。

7. 电势能

　　电荷在电场中所具有的势能叫电势能，用符号 $E_p$ 表示。

　　与重力势能一样，电荷的电势能与零势能点的选取有关。电荷在电场中某一点电势能大小，等于电荷从这一点移动到零电势能点时静电力对它做的功。

　　将电荷在电场中的 $A$ 点移动到 $B$ 点，类似式 11，可以得到静电力做功与电势能变化的关系为

\begin{equation} W_{AB}=E_{pA}-E_{pB}~. \end{equation}

静电力做正功时，电荷的电势能减小；静电力做负功时，电荷的电势能增加。

8. 电势

　　电荷在电场中某一点的电势能与其电荷量的比值，叫做电势，用 $\varphi$ 表示。电势的单位为伏特（简称伏），符号为 $\mathrm{V}$，$1\mathrm{V}=1\mathrm{J/C}$。电势是一个标量。

\begin{equation} \varphi = \frac{E_p}{q}~. \end{equation}

　　同一点的电势与零电势能位置的选取有关，定义了零电势能点后，该点的电势为零。

　　电场线的方向指向电势降落的方向。选取无穷远处的电势为零，在正电荷产生的电场中电势都为正值，越靠近场源电荷电势越高，负电荷则反之。

9. 电势差

　　电场中两点之间电势的差值叫做电势差（或电压），用 $U$ 表示。电势差是一个标量，表示两点间电势的高低关系。如 $A$ 和 $B$ 两点间的电压可表示为

\begin{equation} U_{AB}=\varphi_A - \varphi_B~. \end{equation}

　　若 $W_{AB} < 0$，则表示 $A$ 点的电势比 $B$ 点的电势低。

　　结合式 7 、式 8 和式 9 可知，电荷在电场中从 $A$ 点移动至 $B$ 点时有

\begin{equation} U_{AB} = \frac{W_{AB}}{q}~. \end{equation}

　　由上式可以看出，$U_{AB}$ 的数值等于单位正电荷从 $A$ 点移动至 $B$ 点是静电力所做的功。

　　再结合式 6 和式 10 可得，在匀强电场中，两点之间的电势差等于电场强度与这两点沿电场方向的距离的乘积，即

\begin{equation} U=Ed~. \end{equation}

10. 等势面

　　由电场中电势相同的点所组成的面叫做等势面，任何两个等势面都不会相交。

　　在等势面上任意两点的电势差为零，则电荷在等势面上运动时，静电力不做功。

　　在匀强电场中，各等势面是相互平行的平面。

1. ^ 详见 “物理学常数”