静电场的应用（高中）

贡献者： kahoyip

本文处于草稿阶段。
本文存在未完成的内容。

预备知识　静电场

1. 电容器

　　 电容器是用来储存电荷的电学元件。电容器由两个相互靠近、彼此绝缘的导体组成，两导体间可填充绝缘物质——电介质（空气也是一种电介质）。最简单的电容器由两块相距很近的平行金属板（极板）组成，叫做平行板电容器。实际上，任何彼此绝缘又相隔很近的导体，都可以看成一个电容器。

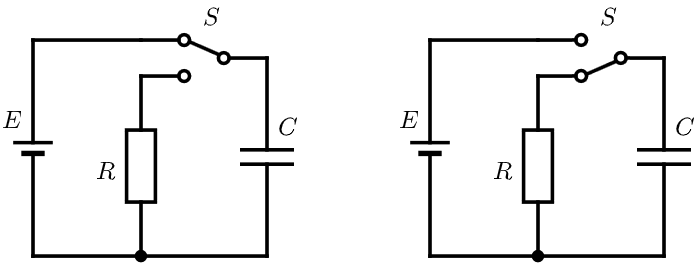
　　电路中，电容器用字母 $C$ 表示，符号如图 1 .

图 1：固定电容器（左）和可变电容器（右）

电容器的充电和放电

　　使得两个极板分别带上等量异种电荷的过程，就是电容器的充电过程。充电过程中，流入正极板的电流逐渐减小，电容器所带的电荷量逐渐增加，电容器两极板之间的电场强度逐渐增强，板间电压也逐渐升高，电容器从电源获得的电能转化为电容器中的电场能。充电结束后，电容器两极板间电压与充电电压相等。

　　使电容器两极板的异种电荷中和的过程，就是电容器的放电过程。放电过程中，电流从正极板流出且逐渐减小，电容器所带的电荷量逐渐减少，电容器两极板间的电场强度逐渐减弱，板间电压也逐渐降低，电容器中的电场能转化为其他形式的能量。

图 2：电容器的充电（左）和放电（右）

电容

　　电容器所带电量 Q 与电容器两极板间电压之比，叫做电容器的电容，用 $C$ 表示，即

\begin{equation} C=\frac{Q}{U}~. \end{equation}

　　在国际单位中，电容的单位是法拉，简称法，符号为 $\mathrm{F}$。

　　常用的电容单位有微法（$\mathrm{\mu F}$）和皮法（$\mathrm{pF}$）。$1\mathrm{F}=10^6 \mathrm{\mu F}=10^{12} \mathrm{pF}$。

　　电容是表示电容器容纳电荷本领的物理量。

电容的串联和并联

　　 $n$ 个电容器并联时，有¹

\begin{equation} C=\sum_{i=1}^{n}C_i~. \end{equation}

　　 $n$ 个电容器串联时，有

\begin{equation} \frac{1}{C}=\sum_{i=1}^{n}\frac{1}{C_i}~. \end{equation}

平行板电容器

　　平行板电容器的电容为

\begin{equation} C = \frac {\epsilon_r S}{4\pi kd}~. \end{equation}

　　式 4 中的 $S$ 和 $d$ 分别为电容器两极板的正对面积和板间距离；$k$ 为静电力常量（式 3 ）；$\epsilon_r$ 为相对介电常数，真空的 $\epsilon_r$ 值为 $1$。

2. 带电粒子在电场中的运动

　　分析带电粒子在电场中的运动时，如电子、质子、离子、$\alpha$ 粒子等，一般都会忽略其重力；而对于带电的小球、粉尘、油滴（液滴）等颗粒，一般都不能忽略其重力。此外，若明确带电粒子所受的静电力远大于重力时，忽略其重力对运动的影响。

带电粒子在电场中的直线运动

例 1　

　　如图 3 所示，两平行金属板间电压恒为 $U$，板间距为 $d$。一带电量为 $q$、质量为 $m$ 的带正电粒子，在仅受静电力的作用下，由静止开始从正极板向负极板运动，求粒子到达负极板时的速度大小 $v$。

图 3：带电粒子在电场中的直线运动

从匀加速直线运动来看，粒子运动时的加速度大小为
\begin{equation} a = \frac{F}{m} = \frac{Eq}{m} = \frac{qU}{md}~. \end{equation}
根据速度与位移的关系可列式
\begin{equation} v^2 - 0 = 2ad~. \end{equation}
从静电力做功来看，根据动能定理 $W=E_{k2}-E_{k1}$ 可列式
\begin{equation} W=qEd=qU=\frac12 mv^2 - 0~. \end{equation}

　　由上述两种方法，可解得粒子到达负极板时的速度大小为

\begin{equation} v = \sqrt{\frac{2qU}{m}}~. \end{equation}

　　当带电粒子沿着一条平直电场线的方向进入电场，在仅受静电力的作用时，粒子的运动为直线运动，若电场为匀强电场，粒子做匀变速直线运动；若电场为非匀强电场，粒子做变加速直线运动。

带电粒子在匀强电场中的偏转

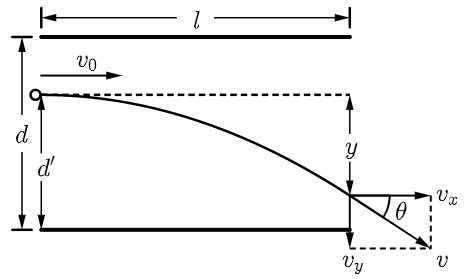
　　两平行金属板间电压恒为 $U$，板间距为 $d$，板长为 $l$。一带电量为 $q$、质量为 $m$ 的带电粒子（重力忽略不计），以初速度 $v_0$ 沿垂直于电场线方向飞入板间的匀强电场。

图 4：带电粒子在匀强电场中的偏转

　　带电粒子进入匀强电场后，仅受到垂直于初速度方向恒定的静电力，带电粒子在匀强电场的运动类似于平抛运动。

由于重力忽略不计，带电粒子在电场中运动的加速度大小为
\begin{equation} a = \frac{F}{m} = \frac{Eq}{m} = \frac{qU}{md}~. \end{equation}
若带电粒子能飞出电场，则带电粒子在电场中的运动时间为
\begin{equation} t = \frac{l}{v_0}~. \end{equation}
带电粒子在静电力方向的位移大小为
\begin{equation} y = \frac12 at^2 = \frac{qUl^2}{2mv_0^2 d}~. \end{equation}
若带电粒子不能飞出电场，则带电粒子将打在极板上，设带电粒子进入电场时与该极板的距离为 $d_0$，则
\begin{equation} y = d_0 = \frac12 at^2 = \frac{qUt^2}{2md}~, \end{equation}

\begin{equation} t = \sqrt{\frac{2mdd_0}{qU}}~. \end{equation}
带电粒子在初速度方向的位移大小为
\begin{equation} x = v_0\sqrt{\frac{2mdd_0}{qU}}~. \end{equation}
带电粒子在静电力方向的分速度大小为
\begin{equation} v_y = at = \frac{qUl}{mv_0d}~. \end{equation}
对于速度偏转角 $\theta$，有
\begin{equation} \tan \theta = \frac{v_y}{v_x} = \frac{qUl}{mv_0^2 d}~. \end{equation}
若带电粒子由静止经一个加速电场（电压为 $U_0$）加速后，再进入偏转电场，由式 8 可得带电粒子进入偏转电场的初速度大小为
\begin{equation} v_0 = \sqrt{\frac{2qU_0}{m}}~. \end{equation}
相应地，$y$ 和 $\tan\theta$ 可表示为
\begin{equation} y = \frac{Ul^2}{4U_0d}~, \end{equation}

\begin{equation} \tan\theta = \frac{Ul}{2U_0d}~. \end{equation}
$y$ 和 $\tan\theta$ 与带电粒子的比荷无关，由此可见，若干个电性相同的带电粒子由静止经过一个加速电场加速后，再进入同一个偏转电场，它们的运动轨迹是相同的。

1. ^ 详细证明见 “电容的串联和并联”