机械振动（高中）
贡献者： kahoyip
物体或物体的一部分在某个位置附近所做的往复运动叫做机械振动，简称振动。
1. 简谐运动
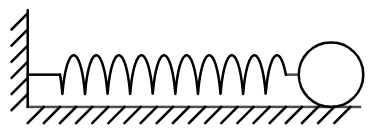
由弹簧和小球组成的系统，叫做弹簧振子，有时也简称为振子。弹簧振子是一种理想模型，研究其运动时，小球被视为质点，并忽略弹簧的质量以及运动过程中的阻力。在弹簧振子的运动过程中，系统的机械能守恒。
图 1 为安置在光滑水平面的弹簧振子，弹簧的一端被固定。弹簧处于自然状态时，小球静止，所受合力为零，此时小球所处的位置叫平衡位置。
当沿水平方向拉动（或推动）小球使其偏离平衡位置并释放，小球将在平衡位置的两侧做往复运动（振动）。振动过程中，小球在竖直方向上所受合力为零，在水平方向上受到弹簧弹力 $ \boldsymbol{\mathbf{F}} $ 的作用。弹力 $ \boldsymbol{\mathbf{F}} $ 的方向与偏离平衡位置的位移 $ \boldsymbol{\mathbf{x}} $ 的方向相反，总是指向平衡位置，其作用是将小球拉回平衡位置，这个力 $ \boldsymbol{\mathbf{F}} $ 叫做回复力。以图 1 向右为正方向，根据胡克定律可知：
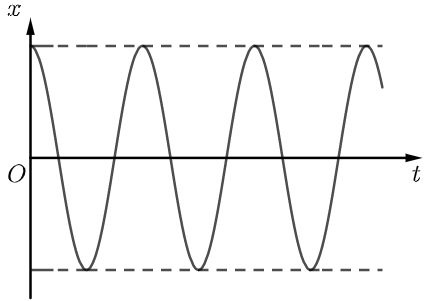
物体在满足式 1 的回复力作用下发生的运动，叫做简谐运动（简谐振动），其位移与时间的关系遵循正弦或余弦函数的规律。简谐运动的位移—时间表达式为：
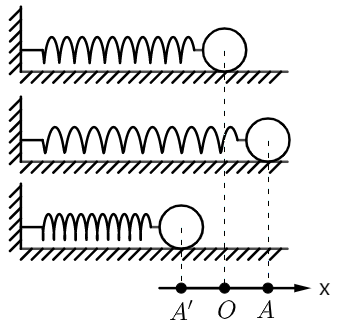
由式 2 可知简谐运动是一个周期性往复运动。振动物体经历 $A$→$O$→$A'$→$O$→$A$ 这样一个完整的振动过程，叫全振动。
| 过程或位置 | 各物理量的变化情况 |
| $A$ | $ \boldsymbol{\mathbf{x}} $ 向右，达最大值；$ \boldsymbol{\mathbf{F}} $ 及 $ \boldsymbol{\mathbf{a}} $ 向左，达最大值；$E_k$ 为零，$E_p$ 达最大值 |
| $A$→$O$ | $ \boldsymbol{\mathbf{x}} $ 向右，减小；$ \boldsymbol{\mathbf{F}} $ 及 $ \boldsymbol{\mathbf{a}} $ 向左，减小；$ \boldsymbol{\mathbf{v}} $ 向左，增大；$E_k$ 增大，$E_p$ 减小 |
| 首次经过 $O$ | $ \boldsymbol{\mathbf{x}} $、$ \boldsymbol{\mathbf{F}} $ 及 $ \boldsymbol{\mathbf{a}} $ 为零；$ \boldsymbol{\mathbf{v}} $ 向左，达最大值；$E_k$ 达最大值，$E_p$ 为零 |
| $O$→$A'$ | $ \boldsymbol{\mathbf{x}} $ 向左，增大；$ \boldsymbol{\mathbf{F}} $ 及 $ \boldsymbol{\mathbf{a}} $ 向右，增大；$ \boldsymbol{\mathbf{v}} $ 向左，减小；$E_k$ 减小，$E_p$ 增大 |
| $A'$ | $ \boldsymbol{\mathbf{x}} $ 向左，达最大值；$ \boldsymbol{\mathbf{F}} $ 及 $ \boldsymbol{\mathbf{a}} $ 向右，达最大值；$E_k$ 为零，$E_p$ 达最大值 |
| $A'$→$O$ | $ \boldsymbol{\mathbf{x}} $ 向左，减小；$ \boldsymbol{\mathbf{F}} $ 及 $ \boldsymbol{\mathbf{a}} $ 向右，减小；$ \boldsymbol{\mathbf{v}} $ 向右，增大；$E_k$ 增大，$E_p$ 减小 |
| 第二次经过 $O$ | $ \boldsymbol{\mathbf{x}} $、$ \boldsymbol{\mathbf{F}} $ 及 $ \boldsymbol{\mathbf{a}} $ 为零；$ \boldsymbol{\mathbf{v}} $ 向右，达最大值；$E_k$ 达最大值，$E_p$ 为零 |
| $O$→$A$ | $ \boldsymbol{\mathbf{x}} $ 向右，增大；$ \boldsymbol{\mathbf{F}} $ 及 $ \boldsymbol{\mathbf{a}} $ 向左，增大；$ \boldsymbol{\mathbf{v}} $ 向右，减小；$E_k$ 减小，$E_p$ 增大 |
$ \boldsymbol{\mathbf{x}} $ 为小球偏离平衡位置的位移，$ \boldsymbol{\mathbf{F}} $ 及 $ \boldsymbol{\mathbf{a}} $ 分别为小球所受回复力及加速度，$ \boldsymbol{\mathbf{v}} $ 为小球的运动速度，$E_k$ 和 $E_p$ 分别对应小球的动能和弹簧的势能。
2. 匀速圆周运动和简谐运动的联系
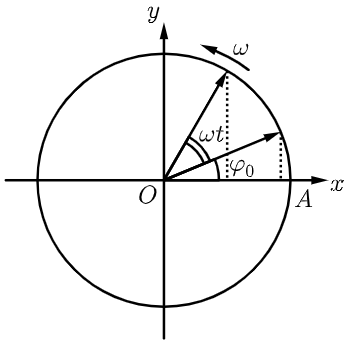
质量为 $m$ 的质点绕点 $O$ 做半径为 $A$、角速度为 $\omega$ 的匀速圆周运动（图 3 ），$t=0$ 时质点与点 $O$ 的连线与 $x$ 轴的夹角为 $\varphi_0$。质点相对圆心 $O$ 的位移在 $x$ 轴上的投影为 $x=A \cos\left(\omega t + \varphi_0\right) $，可见做匀速圆周运动的质点在直径上的投影的运动是简谐运动。
质点在上述匀速圆周运动的向心加速度大小为 $a=\omega^2 A$，向心加速度在 $x$ 轴的投影为 $a_x=-\omega^2 A \cos\left(\omega t + \varphi_0\right) $，即为简谐运动的加速度，则简谐运动的回复力可表示为
简谐运动的振动周期
3. 单摆
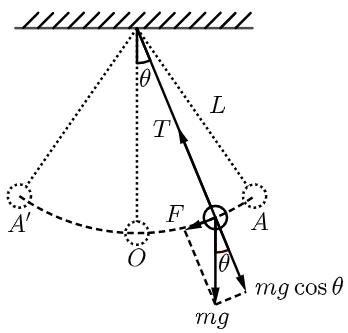
一根质量和伸缩量可以忽略不计的细绳（摆线），上端固定，下端系着一个看作质点的物体（摆球），就构成了一个单摆。单摆是实际摆的理想模型，摆球的运动是以摆线固定点为圆心的变速圆周运动，也是在平衡位置1两侧的周期性往复振动，运动过程中机械能守恒。
单摆运动时的受力分析如图 4 所示，摆球受到了重力和摆线拉力作用。摆线的拉力和摆球重力沿径向的分力的合力 $T-mg\cos\theta$ 提供了摆球做圆周运动的向心力，摆球重力沿圆弧切线方向的分力 $mg\sin\theta$ 提供了摆球振动的回复力。
当摆角 $\theta$ 很小时，有 $\sin\theta \approx \theta$2，摆球的位移大小 $x$ 近似于 $L\theta$，可得回复力 $F \approx -mgx/L$，符合式 1 的形式，此时可把单摆的摆动近似看成简谐运动，将 $k=mg/L$ 代入式 5 可得单摆做简谐运动的周期为
4. 受迫振动和共振
从上述内容可以知道，弹簧振子和单摆在不受外力时做简谐运动，其振动周期和频率只与自身的性质有关，这种振动系统不受外力的振动叫做固有振动，对应的振动频率叫做固有频率。
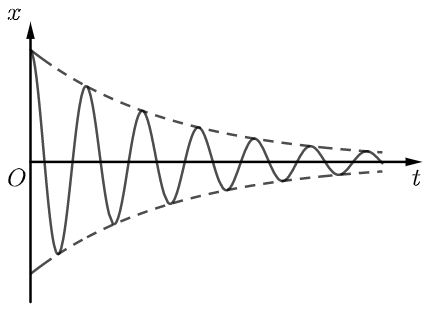
实际的振动会受到阻力的作用，系统因克服阻力做功而消耗机械能，振幅逐渐减小。振幅随时间减小的振动，叫做阻尼振动。阻尼越大，振幅减小得越快，当阻尼过大时，系统将不能发生振动。
在实际的振动中，为了保持振幅不变，我们通常会给系统施加一个周期性的外界驱动力，由于外界驱动力的作用，系统机械能得以补充，并持续振动。系统在周期性的外界驱动力作用下的振动，叫做受迫振动。当系统所做的受迫振动达稳定后，其振动频率等于驱动力的频率，与固有频率无关。
当驱动力的频率等于系统的固有频率时，系统所做受迫振动的振幅最大，这种现象叫做共振，如音叉共鸣实验所演示的就是声音的共振现象。
1. ^ 单摆自然悬挂时摆球的位置，单摆运动过程中的最低点
2. ^ 参考：小角极限（简明微积分）