贡献者: FFjet; addis
我们之前已经接触过了实函数的积分,那么我们如何推广到复数上呢?实际上,同高等数学一样,也采用 “分割”、“求和”、“取极限” 的步骤来定义积分。
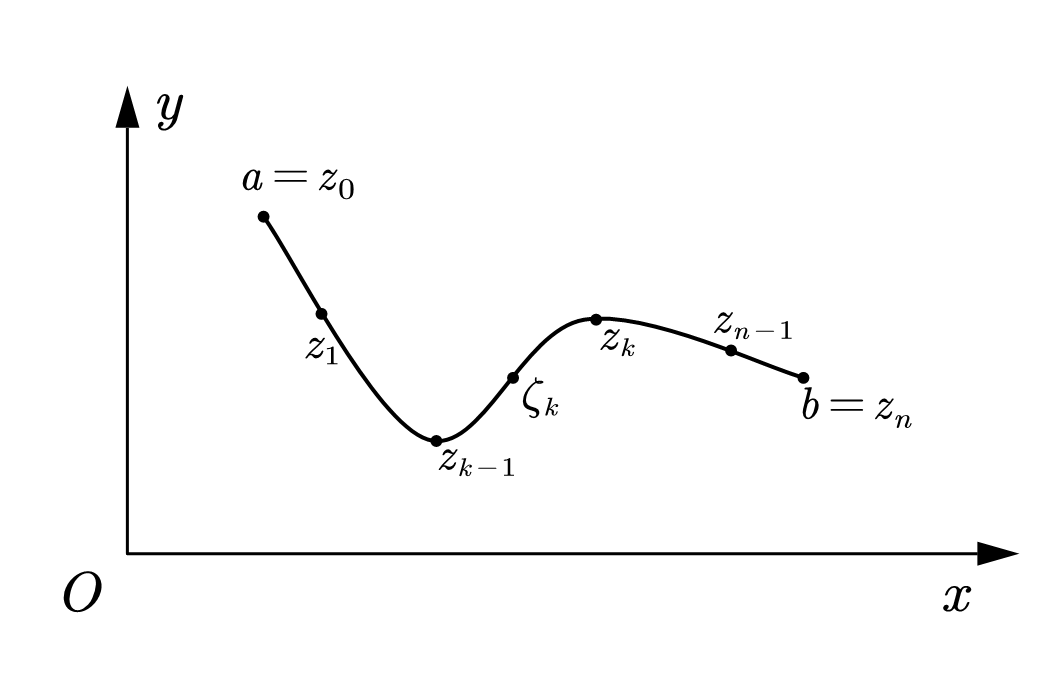
图 1:复积分的定义
定义 1 复积分的定义
设 $C$ 为复平面上一条起点在 $a$,终点在 $b$($a,b\in\mathbb C$)的有向曲线,其方程为
\begin{equation}
z(t)=x(t)+\mathrm{i} y(t) \qquad(t_a \leqslant t \leqslant t_b)~.
\end{equation}
函数 $f(z)$ 定义在 $C$ 上。用一组点 $z_{0}, z_{1}, \dots, z_{n}$ 沿曲线从 $a$ 到 $b$ 对曲线 $C$ 进行分割。当 $n$ 不断增加,设 $\Delta z_{k}=z_{k}-z_{k-1}$,$\zeta_k$ 为 $z_{k-1},z_k$ 之间任意一点,分割 $C$ 所得各个弧段长度中的最大值 $d$,不论对 $C$ 的分法及 $\zeta_k$ 的取法如何,若存在极限
\begin{equation}
S = \lim_{d \rightarrow 0} \sum_{k=1}^{n} f\left(\zeta_{k}\right) \Delta z_{k}~,
\end{equation}
则称 $f(z)$ 沿 $C $(从 $a$ 到 $b$)
可积,称 $S$ 为 $f(z)$ 沿 $C$(从 $a$ 到 $b$)的积分,记作
\begin{equation}
S=\int_{C} f(z) \mathrm{d} z~.
\end{equation}
其中 $f (z)$ 称为
被积函数,$C$ 称为
积分路径。
现在来看一下用定义计算复积分的一个简单例子。
例 1
设 $C$ 是一条起点为 $a$ 终点为 $b$ 的曲线,试计算 $\displaystyle S=\int_C\mathrm dz$。
解:用定义来计算该积分。由定义,将 $f(z)=1$ 代入,得:
\begin{equation}
\int_{C} \mathrm{d} z=\lim _{d \rightarrow 0} \sum_{k=1}^{n}\left(z_{k}-z_{k-1}\right)= b-a~.
\end{equation}
通过这道例题,我们发现对于函数 $f(z)=1$,它的积分值只依赖于积分路径 $C$ 的起点 $a$ 和终点 $b$,而与积分路径的形状是无关的。这个性质对于更一般的 $f$ 是否成立?在后面的柯西积分定理中,我们将给出答案。
有了积分定义后,最先关心的问题是:积分存在的条件,积分的性质与积分的计算。下面就来讨论这几个问题。
1. 复积分与线积分
定理 1
令复平面的实轴为 $x$ 轴,虚轴为 $y$ 轴,用两个二元实函数 $u, v$ 来表示 $f(z)$
\begin{equation}
f (z) = u(x, y) + \mathrm iv(x, y)~,
\end{equation}
令两个矢量场为($ \boldsymbol{\mathbf{r}} $ 为 $xy$ 平面上的位置矢量)
\begin{equation}
\boldsymbol{\mathbf{f}} ( \boldsymbol{\mathbf{r}} ) = u \hat{\boldsymbol{\mathbf{x}}} - v \hat{\boldsymbol{\mathbf{y}}}
\qquad
\boldsymbol{\mathbf{g}} ( \boldsymbol{\mathbf{r}} ) = v \hat{\boldsymbol{\mathbf{x}}} + u \hat{\boldsymbol{\mathbf{y}}} ~,
\end{equation}
那么积分 $\int_{C} f(z) \mathrm{d} z$ 的实部和虚部分别可以看作两个矢量场 $ \boldsymbol{\mathbf{f}} ( \boldsymbol{\mathbf{r}} ), \boldsymbol{\mathbf{g}} ( \boldsymbol{\mathbf{r}} )$ 在曲线 $C$ 上的线积分
\begin{equation}
\begin{aligned}
\int_{C} f(z) \,\mathrm{d}{z} &= \int_C \boldsymbol{\mathbf{f}} ( \boldsymbol{\mathbf{r}} ) \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } + \mathrm{i} \int_C \boldsymbol{\mathbf{g}} ( \boldsymbol{\mathbf{r}} ) \boldsymbol\cdot \,\mathrm{d}{ \boldsymbol{\mathbf{r}} } \\
&= \int_{C} u \mathrm{d} x-v \mathrm{d} y+\mathrm{i} \int_{C} v \mathrm{d} x+u \mathrm{d} y~.
\end{aligned}
\end{equation}
研究复变函数的积分问题,可以转化为研究实变量的二元实值函数沿曲线 $C$ 的线积分问题。
证明
\begin{equation}
\begin{aligned}
\int_C f(z) \,\mathrm{d}{z} &= \int_C (u+iv)( \,\mathrm{d}{x} + \mathrm{i} \,\mathrm{d}{y} )\\
&= \int_C u \,\mathrm{d}{x} - v \,\mathrm{d}{y} + \mathrm{i} \int_{C} v \mathrm{d} x+u \mathrm{d} y~.
\end{aligned}
\end{equation}
证毕。
2. 复积分的性质与计算
上面我们看到了将线积分和复积分联系起来的。容易想到,线积分的一些性质可移到复变函数的积分上来。
若 $f(z)$ 与 $g(z)$ 沿曲线 $C,C^-$($C^-$ 表示与曲线 $C$ 方向相反的同一条曲线)可积,则有
\begin{equation}
\int_{C} A f(z) \mathrm{d} z=A \int_{C} f(z) \mathrm{d} z \quad(A \text { 为复常数 })~,
\end{equation}
\begin{equation}
\int_{C}[Af(z)+ Bg(z)] \mathrm{d} z= A\int_{C} f(z) \mathrm{d} z + B\int_{C} g(z) \mathrm{d} z~,
\end{equation}
\begin{equation}
\int_{C} f(z) \mathrm{d} z=-\int_{C^{-}} f(z) \mathrm{d} z~,
\end{equation}
\begin{equation}
\int_{C} f(z) \mathrm{d} z=\int_{C_{1}} f(z) \mathrm{d} z+\int_{C_{2}} f(z) \mathrm{d} z \quad\left(C \text{ 由 } C_{1} \text{ 与 } C_{2} \text { 首尾相接而成}\right)~.
\end{equation}
设 $ L$ 为曲线 $C$ 的长度,若 $f (z)$ 沿 $C$ 可积,且在 $C$ 上满足 $ \left\lvert f(z) \right\rvert \leqslant M $,则
\begin{equation}
\left|\int_{c} f(z) \mathrm{d} z\right| \leqslant \int_{c}|f(z)| \mathrm{d} s \leqslant M L~.
\end{equation}
该式提供了一种估计复变函数积分的模的方法。
未完成:以下待审阅
到现在为止,计算复变函数积分只有两种方法,一是定义,二是。有无其他方法呢?
我们注意到,由于积分路径常取光滑曲线(或逐段光滑曲线),所以 $ f (z) $ 沿曲线 $C $ 的积分可归结为 $f [z(t)]$ 关于曲线 $C$ 的参数的积分。
事实上,若 $C$ 为光滑曲线(或逐段光滑曲线)
\begin{equation}
\begin{aligned} z &=z(t) \\ &=x(t)+\mathrm{i} y(t),(t_a \leqslant t \leqslant t_b)~. \end{aligned}
\end{equation}
则 $z^\prime(t)$ 在 $[t_a, t_b]$ 上连续,且 $z^\prime(t) = x^\prime(t) + \mathrm iy^\prime(t) \neq 0$。再设 $ f (z)$ 在 $C$ 上连续及
\begin{equation}
\begin{aligned} f[z(t)] &=u[x(t), y(t)]+\mathrm{i} v[x(t), y(t)] \\ &=u_{1}(t)+\mathrm{i} v_{1}(t)~. \end{aligned}
\end{equation}
则有
\begin{equation}
\begin{aligned} \int_{C} f(z) \mathrm{d} z &=\int u \mathrm{d} x-v \mathrm{d} y+\mathrm{i} \int_{C} v \mathrm{d} x+u \mathrm{d} y \\ &=\int_{t_a}^{t_b}\left\{u[x(t), y(t)] x^{\prime}(t)-v[x(t), y(t)] y^{\prime}(t)\right\} \mathrm{d} t+\\ & \mathrm{i} \int_{t_a}^{t_b}\left\{v[x(t), y(t)] x^{\prime}(t)+u[x(t), y(t)] y^{\prime}(t)\right\} \mathrm{d} t \\ &=\int_{t_a}^{t_b}\left[u_{1}(t)+\mathrm{i} v_{1}(t)\right]\left[x^{\prime}(t)+\mathrm{i} y^{\prime}(t)\right] \mathrm{d} t \\ &=\int_{t_a}^{t_b} f[z(t)] \mathrm{d} t ~.\end{aligned}
\end{equation}
这样一来,便将 $ f (z)$ 沿曲线 $C$ 的积分归结为 $ f (z)$ 关于曲线 $C$ 的参数 $t$ 的积分。
用式 16 来计算积分 $\displaystyle \int_{C} f(z) \mathrm{d} z$ 包含三个步骤:
- 写出曲线 $C$ 的方程 $z=z(t)=x(t)+i y(t), t_a \leqslant t \leqslant t_b$
- 将 $ z = z(t)$ 与 $\mathrm{d}z = z^\prime (t)\mathrm{d}t $ 代入所求积分 $\displaystyle \int_{c} f(z) \mathrm{d} z$ 中
- 计算式 16 右端的关于参数 $t$ 的积分。
有了上述求复变函数的积分的方法之后,我们一起来看几个例子,并尝试用不同的方法来求解。
例 2
计算 $\displaystyle \int _ C z \mathrm dz$,其中 $C$ 为起点在 $a$ 终点在 $b$ 的一条逐段光滑曲线。
我们用定义来计算一下。
由题知,$f(z)=z$。取 $\zeta_k=z_{k-1}$,则 $f\left(\zeta_{k}\right)=z_{k-1}$,作和:
\begin{equation}
A_{n}=\sum_{k=1}^{n} f\left(\zeta_{k}\right) \Delta z_{k}=\sum_{k=1}^{n} z_{k-1}\left(z_{k}-z_{k-1}\right)~.
\end{equation}
因 $f(z)=z$ 在 $C$ 上连续,所以积分一定存在,于是
\begin{equation}
\int_{C} f(\mathrm{z}) \mathrm{d} \mathrm{z}=\lim _{n \rightarrow \infty \atop d \rightarrow 0} A_{n}~.
\end{equation}
另外,若取 $\zeta_k=z_k$,则 $f\left(\zeta_{k}\right)=z_{k}$,作和:
\begin{equation}
B_{n}=\sum_{k=1}^{n} f\left(\zeta_{k}\right) \Delta z_{k}=\sum_{k=1}^{n} z_{k}\left(z_{k}-z_{k-1}\right)~.
\end{equation}
由之前的讨论知,
\begin{equation}
\int_{C} f(\mathrm{z}) \mathrm{d} \mathrm{z}=\lim _{n \rightarrow \infty \atop d \rightarrow 0} B_{n}~.
\end{equation}
由
式 18 和
式 20 知,
\begin{equation}
\begin{aligned} \int_{C} f(z) \mathrm{d} z &=\frac{1}{2} \lim _{n \rightarrow \infty \atop d \rightarrow 0}\left(A_{n}+B_{n}\right) \\ &=\frac{1}{2}\left(b^{2}-a^{2}\right)~. \end{aligned}
\end{equation}
我们再次发现:$f (z) = z$ 也有一个和 $f(z)=1$ 一样好的性质:它沿曲线 $C$ 的积分只依赖于起点与终点,而与 $C $ 的形状无关!
例 3
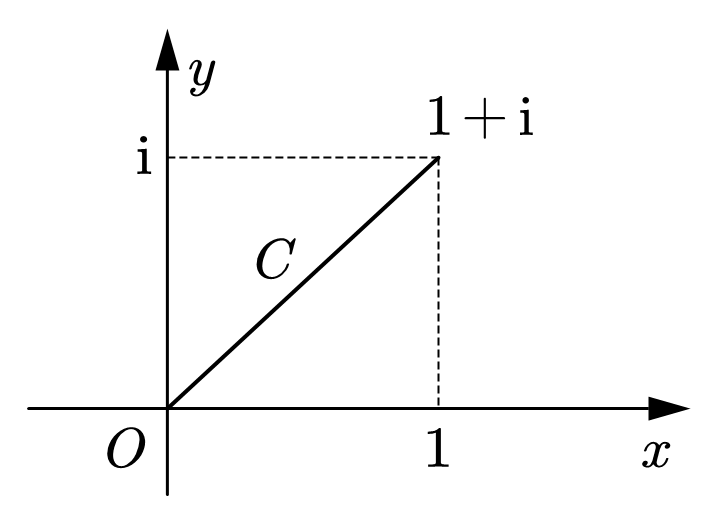
试计算 $\displaystyle \int_{C} x \mathrm{d} z$,其中 $C$ 为起点在 $z = 0$,终点在 $z =1+\mathrm i$ 的直线段。
图 2:积分路径
我们用式 16 计算。首先,写出 $C$ 的方程为
\begin{equation}
z=z(t)=(1+i) t \qquad (0 \leqslant t \leqslant 1)~.
\end{equation}
由 $x+\mathrm{i} y=z=z(t)=(1+\mathrm{i}) t$ 得 $\mathrm{d} z=z^{\prime}(t) \mathrm{d} t=(1+\mathrm{i}) \mathrm{d} t$,将 $x=t$ 和 $\mathrm dz$ 代入所求积分,得
\begin{equation}
\int_{C} x \mathrm{d} z=\int_{0}^{1}(1+\mathrm{i}) t \mathrm{d} t~,
\end{equation}
最后,计算上式右端的积分得
\begin{equation}
\int_{C} x \mathrm{d} z=\frac{1+\mathrm{i}}{2}~.
\end{equation}
例 4
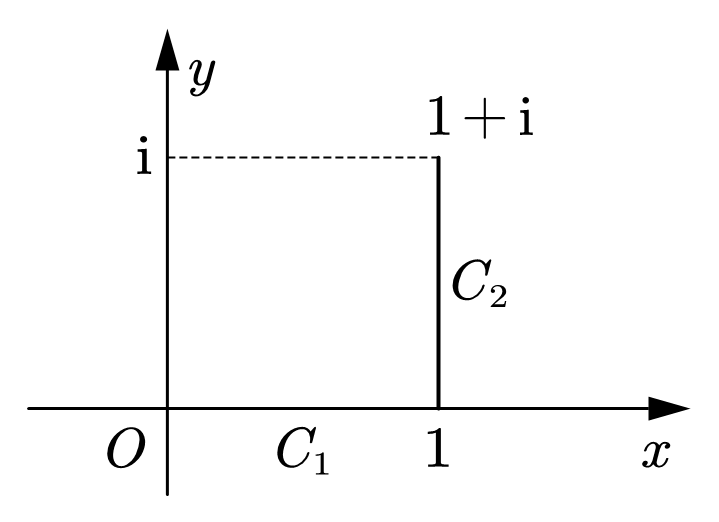
设 $\Gamma$ 为由 $C_1$ 与 $C_2$ 首尾相接而成的起点在 $z=0$,终点在 $ z =1+ \mathrm i $ 的曲线,如图 3 所示。计算 $\displaystyle \int_{\Gamma} x \mathrm{d}z$。
图 3:积分路径
首先写出 $C_1$ 和 $C_2$ 的方程为
\begin{equation}
\begin{array}{l}C_{1}: z=z(t)=t(0 \leqslant t \leqslant 1) \\ C_{2}: z=z(t)=1+\text { i }t(0 \leqslant t \leqslant 1)~.\end{array}
\end{equation}
下面分别计算 $C_1$ 和 $C_2$。
在 $C_1$ 上有 $x=t, \mathrm{d} z=\mathrm{d} t$,代入 $\displaystyle \int_{C_{1}} x \mathrm{d} z$ 得 $\displaystyle \int_{C_{1}} x \mathrm{d} z=\int_{0}^{1} t \mathrm{d} t$。在 $C_2$ 上有 $\displaystyle x=\operatorname{Re} z(t)=1, \mathrm{d} z=\mathrm{id} t$,代入 $\displaystyle \int_{C_{2}} x \mathrm{d} z$ 得到 $\displaystyle \int_{C_{2}} x \mathrm{d} z=\int_{0}^{1} \mathrm{id} t$。
最后,计算积分得
\begin{equation}
\int_{\Gamma} x \mathrm{d} z=\int_{C_{1}} x \mathrm{d} z+\int_{C_{2}} x \mathrm{d} z=\int_{0}^{1} t \mathrm{d} t+\int_{0}^{1} \mathrm{i} \mathrm{d} t=\frac{1}{2}+\mathrm{i}~.
\end{equation}
比较例 3 和例 4 ,我们发现,对于复变函数 $f(z)=x$,积分的结果却与积分路径的选取很有关系。
再来介绍一个十分重要的例题。
例 5
试证:
\begin{equation}
\oint_{C} \frac{1}{(z-a)^{n}}=
\left\{\begin{aligned}
&2 \pi \mathrm{i} && (n=1) \\
&0 && (n \neq 1 \text{且为整数})~.
\end{aligned}\right. \end{equation}
其中 $C$ 是为以 $a $ 为圆心,以 $R $ 为半径的圆周。
证明:这里的 $C $ 是一条围线,对于沿围线的积分,若无特殊声明,则今后总理解为沿围线的正向积分。
用计算积分的方法来证明本题。
首先,写出 $C $ 的方程为
\begin{equation}
\begin{aligned} z &=z(t) \\ &=a+R \mathrm{e}^{\mathrm{i} \theta} \quad(0 \leqslant \theta \leqslant 2 \pi) ~.\end{aligned}
\end{equation}
其次,$\mathrm{d} z=\mathrm{i} R \mathrm{e}^{\mathrm{i} \theta} \mathrm{d} \theta$,被积函数当 $n =1$ 时为 $(z-a)^{-1}=R^{-1} \mathrm{e}^{-\mathrm{i} \theta}$,当 $n \ne 1$ 且为整数时,为 $(z-a)^{-n}=R^{-n} \mathrm{e}^{-\mathrm{i} n \theta}$
再次,计算积分,$n=1$ 时,有
\begin{equation}
\begin{aligned} \oint_{c} \frac{1}{z-a} \mathrm{d} z &=\int_{0}^{2 \pi} \frac{\mathrm{i} R \mathrm{e}^{\mathrm{i} \theta}}{R \mathrm{e}^{\mathrm{i} \theta}} \mathrm{d} \theta \\ &=2 \pi \mathrm{i} \end{aligned}~.
\end{equation}
当 $n \neq 1$ 且为整数时,有
\begin{equation}
\begin{aligned} \oint_{C} \frac{1}{(z-a)^{n}} \mathrm{d} z &=\int_{0}^{2 \pi} \frac{\mathrm{i} R \mathrm{e}^{\mathrm{i} \theta}}{R^{n} \mathrm{e}^{\mathrm{i} n \theta}} \mathrm{d} \theta \\ &=\frac{\mathrm{i}}{R^{n-1}} \int_{0}^{2 \pi} \mathrm{e}^{-\mathrm{i}(n-1) \theta} \mathrm{d} \theta \\ &=\frac{\mathrm{i}}{R^{n-1}}\left[\int_{0}^{2 \pi} \cos\left(n-1\right) \theta \mathrm{d} \theta-\mathrm{i} \int_{0}^{2 \pi} \sin\left(n-1\right) \theta \mathrm{d} \theta\right]=0~. \end{aligned}
\end{equation}
综上所述,问题得证。
例 6
计算积分
\begin{equation}
\oint_{|z-1|=1} \frac{z}{z-1} \mathrm{d} z~.
\end{equation}
由积分路径为 $|z -1|=1$,得 $z-1=\mathrm{e}^{\mathrm{i} \theta}(0 \leqslant \theta \leqslant 2 \pi)$。于是,积分路径的方程为
\begin{equation}
z=z(\theta)=1+\mathrm{e}^{\mathrm{i} \theta},(0 \leqslant \theta \leqslant 2 \pi)~.
\end{equation}
故
\begin{equation}
\begin{aligned} \oint_{z-1} \frac{z}{z-1} \mathrm{d} z &=\int_{0}^{2 \pi} \frac{1+\mathrm{e}^{\mathrm{i} \theta}}{\mathrm{e}^{\mathrm{i} \theta}} \mathrm{ie}^{\mathrm{i} \theta} \mathrm{d} \theta \\ &=\int_{0}^{2 \pi} \mathrm{id} \theta+\int_{0}^{2 \pi}(\cos \theta+\mathrm{i} \sin \theta) \mathrm{d} \theta \\ &=2 \pi \mathrm{i} ~.\end{aligned}
\end{equation}
例 7
计算积分
\begin{equation}
\oint_{|z-2|=1} \frac{3 z^{2}}{(z-2)^{3}} \mathrm{d} z~.
\end{equation}
由 $ |z - 2| =1$ 得积分路径的方程为
\begin{equation}
z=z(\theta)=2+\mathrm{e}^{\mathrm{i} \theta},(0 \leqslant \theta \leqslant 2 \pi)~.
\end{equation}
于是
\begin{equation}
\begin{aligned} \oint_{|z-2|=1} \frac{3 z^{2}}{(z-2)^{3}} \mathrm{d} z &=\int_{0}^{2 \pi} \frac{3\left(2+\mathrm{e}^{\mathrm{i} \theta}\right)^{2}}{\left(\mathrm{e}^{\mathrm{i} \theta}\right)^{3}} \mathrm{ie}^{\mathrm{i} \theta} \mathrm{d} \theta \\ &=3 \mathrm{i} \int_{0}^{2 \pi}\left(4 \mathrm{e}^{-\mathrm{i} 2 \theta}+4 \mathrm{e}^{\mathrm{i} \theta}+1\right) \mathrm{d} \theta \\ &=6 \pi \mathrm{i}~. \end{aligned}
\end{equation}