贡献者: addis
1在一个竖直平面上任意取两个不同的点 $P_1, P_2$,$P_1$ 的高度大于等于 $P_2$。一个静止的质点在 $P_1$ 处释放,在恒定的重力的作用下沿某曲线 $\mathcal L$ 的轨道无摩擦地运动到 $P_2$,耗时为 $t$。若一条曲线 $\mathcal L$ 使得 $t$ 最短,那么这个曲线就是 $P_1, P_2$ 两点间的最速降线(brachistochrone)。
通过下文的推导可以发现,最速降线必定是摆线。然而连接两点的摆线有无穷多条,其中只有一条是最速降线。最速降线对应的摆线是起点参数为 $\theta = 0$ 的那条,即初始斜率为无穷大。
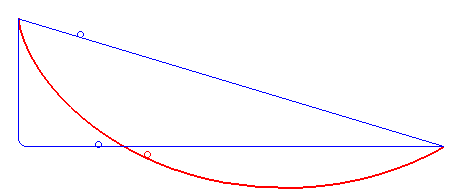
图 1:红色:摆线;蓝色:直线和圆角折线。计算证明摆线最快。
1. 推导
2令 $x$ 轴向右,$y$ 轴向下。质点由原点出发,在重力加速度 $g$ 的作用下沿函数 $y(x)$ 的曲线运动。为书写方便令质量为 $m = 1$。由动能定理得
\begin{equation}
v = \sqrt{2gy}~.
\end{equation}
曲线任意一点得斜率为($y$ 轴向下,$x$ 轴向右)
\begin{equation}
\cos\theta = \frac{1}{\sqrt{1 + \dot{y}^2}}~.
\end{equation}
注意 $\dot{y}$ 代表 $y(x)$ 对 $x$ 求导而不是对时间求导。$x$ 方向速度分量为
\begin{equation}
\frac{\mathrm{d}{x}}{\mathrm{d}{t}} = v\cos\theta~.
\end{equation}
即从 $x_1$ 滑落到点 $x_2$ 的时间为
\begin{equation}
t_{12} = \int_{x_1}^{x_2} \frac{ \,\mathrm{d}{x} }{v\cos\theta} = \int_{x_1}^{x_2} \sqrt{\frac{1 + \dot{y}^2}{2gy}} \,\mathrm{d}{x} ~,
\end{equation}
要求 $t_{12}$ 关于 $y(x)$ 的极值,可以使用拉氏方程,令 “拉格朗日量” 为被积函数
\begin{equation}
L(y, \dot y, x) = \sqrt{\frac{1 + \dot{y}^2}{2gy}}~,
\end{equation}
注意不显含 $x$,即 $ \partial L/\partial x = 0$。下面来一步步代入拉格朗日方程。先把 $L$ 对 $\dot{y}$ 求偏导,注意要把 $y$ 看作常数
\begin{equation}
\frac{\partial}{\partial{\dot{y}}} L(y, \dot{y}, x) = \frac{1}{\sqrt{2gy}}\frac{\dot{y}}{\sqrt{1 + \dot{y}^2}}~.
\end{equation}
然后对 $x$ 求全导数(把 $y, \dot{y}$ 看成 $x$ 的函数)
\begin{equation}
\frac{\mathrm{d}}{\mathrm{d}{x}} \frac{\partial L}{\partial \dot{y}} = \frac{1}{\sqrt{2gy}\sqrt{1+\dot y^2}} \left(-\frac{\dot y^2}{2y} + \ddot y - \frac{\dot y^2 \ddot y}{1 + \dot y^2} \right) ~.
\end{equation}
同理,将 $\dot y$ 看作常数,对 $y$ 求偏导得
\begin{equation}
\frac{\partial L}{\partial y} = -\frac{1}{2} \sqrt{\frac{1 + \dot{y}^2}{2gy}} \frac{1}{y}~.
\end{equation}
以上两式代入拉氏方程(
式 1 ),即令两式相等,并化简得
\begin{equation}
2y\ddot y + \dot y^2 + 1 = 0~.
\end{equation}
令 $z=\dot{y}$,则
式 9 化为
\begin{equation}
2yz \frac{\mathrm{d}{z}}{\mathrm{d}{y}} +z^2+1=0~,
\end{equation}
分离变量得
\begin{equation}
\frac{2z}{z^2+1} \,\mathrm{d}{z} = -\frac{ \,\mathrm{d}{y} }{y}~.
\end{equation}
该方程的解为
\begin{equation}
\frac{y}{a} = 1 - \cos \left[\frac{x + \sqrt{y(2a-y)}}{a} \right] ~,
\end{equation}
其中 $a$ 是大于零的参数。令方括号部分为 $\theta$,该方程能写成 $\theta$ 的参数方程,该曲线被称为
摆线(cycloid)或
滚轮线。
\begin{equation}
\left\{\begin{aligned}
x &= a(\theta - \sin\theta)\\
y &= a(1 - \cos\theta)
\end{aligned}\right. ~.\end{equation}
并且有
\begin{equation}
\dot y = \frac{\sin\theta}{1 - \cos\theta} ~,\qquad
\ddot y = -\frac{1}{a(1-\cos\theta)^2}~,
\end{equation}
代入
式 9 可验证成立。
由于我们一开始假设了起点处 $y_1 = 0$,在式 13 中对应的是滚轮线的任意尖端($\theta_1 = 2\pi n$)。不妨假设起点处 $\theta_1 = 0$,即 $x_1 = 0$。接下来,由于 $(x_2, y_2)$ 必须落在曲线上, $a$ 的值可以由此确定。
代入式 4 得质点沿最速降线滑动的时间为
\begin{equation}
t_{12} = \sqrt{\frac{a}{g}}(\theta_2 - \theta_1) = \sqrt{\frac{a}{g}} \theta_2~,
\end{equation}
其中 $\theta_2$ 为 $x_2, y_2$ 对应的参数。
2. 证明摆线是等时线
摆线有另一个奇妙的性质:对于固定的 $a$,无论从曲线哪个位置释放质点,质点来回振动的周期都是相同的。这个结论可以用于制造精确的钟摆,由惠更斯于 1638 年在 《摆钟论》 中提出,比牛顿的 《原理》(1686)早了约 50 年。
令质点的起始位置对应的参数为 $\theta = \theta_0$,滚动到底部时参数为 $\theta = \pi$。
若不改变坐标系,则所需时间变为3
\begin{equation}
\begin{aligned}
t_{12} &= \int_{x_1}^{x_2} \sqrt{\frac{1 + \dot{y}^2}{2g(y - y_0)}} \,\mathrm{d}{x}
= \int_{x_1}^{x_2} \sqrt{\frac{2/(1 - \cos\theta)}{2ga(\cos\theta_0 - \cos\theta)}} \,\mathrm{d}{x} \\
&= \sqrt{\frac{a}{g}}\int_{\theta_0}^{\pi} \sqrt{\frac{1 - \cos\theta}{\cos\theta_0 - \cos\theta}} \,\mathrm{d}{\theta}
= \pi\sqrt{\frac{a}{g}}~.
\end{aligned}
\end{equation}
可以发现这与 $\theta_0$ 无关,且 $\theta_0 = 0$ 时与
式 15 吻合。所以从摆线的任何位置释放周期都相同。摆动周期为
\begin{equation}
T = 4\pi\sqrt{\frac{a}{g}}~.
\end{equation}
这相当于摆长为 $2a$ 的
单摆的小幅摆动周期,因为摆线底部的
曲率半径是 $2a$。
1. ^ 参考 Wikipedia 相关页面。
2. ^ 参考 Wolfram MathWorld 相关页面,以及 [1] 的相关章节。
3. ^ 最后一步积分笔者使用了 Mathematica。
[1] ^ Herbert Goldstein. Classical Mechanics 3ed