仿射法在解析几何中的应用
贡献者: 赵淦是
- 本文存在未完成的内容。 {缺少仿射变换的一般定义及性质证明}
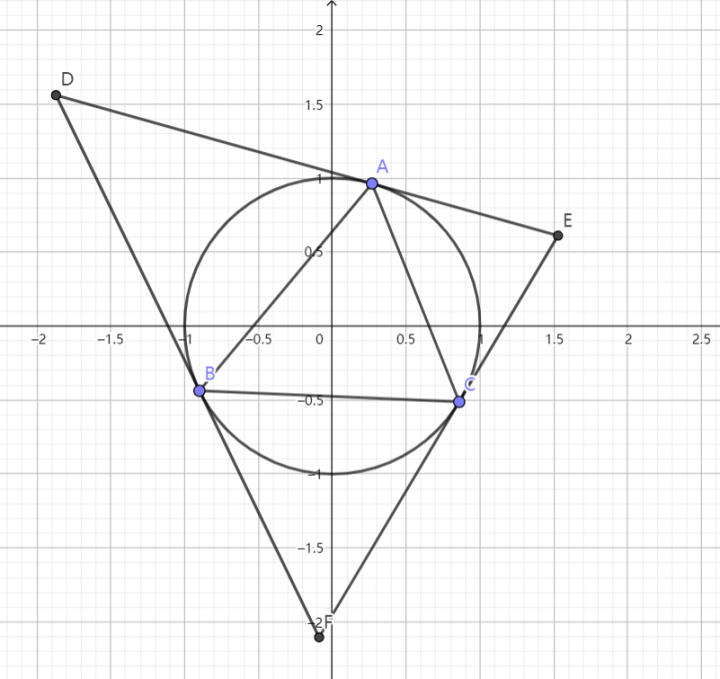
1. 引例:2022 年全国乙卷解析几何大题
已知椭圆 $\displaystyle{E}$ 的中心为坐标原点,对称轴为 $\displaystyle{x}$ 轴、$\displaystyle{y}$ 轴,且过 $\displaystyle{A(0,-2)}$,$\displaystyle{B\left(\frac{3}{2},-1\right)}$ 两点。
(1)求 $\displaystyle{E}$ 的方程;
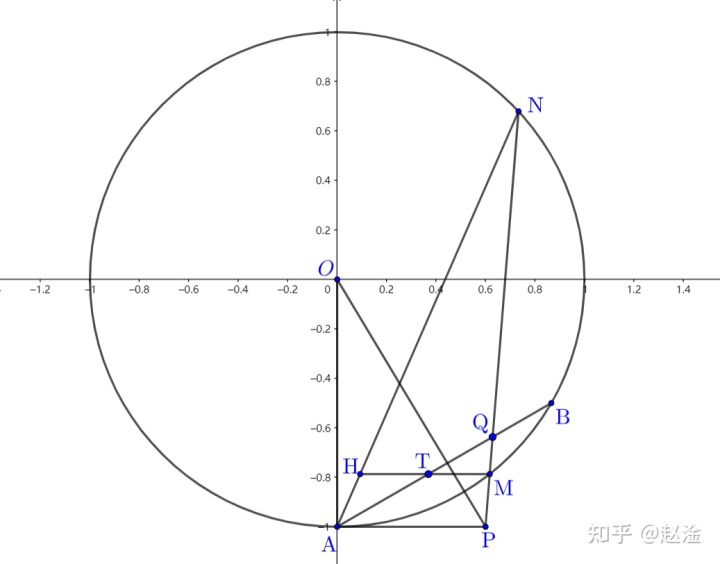
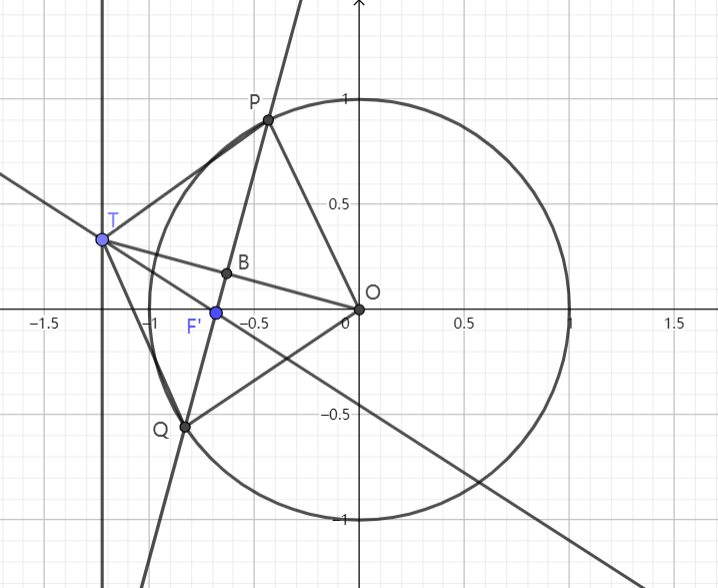
(2)设过点 $\displaystyle{P(1,-2)}$ 的直线交 $\displaystyle{E}$ 于 $\displaystyle{M,N}$ 两点,过 $\displaystyle{M}$ 且平行于 $\displaystyle{x}$ 轴的直线与线段 $\displaystyle{AB}$ 交于点 $\displaystyle{T}$。点 $\displaystyle{H}$ 满足 $\displaystyle{\overrightarrow{MT}=\overrightarrow{TH}}$,证明:直线 $\displaystyle{HN}$ 过定点。
解:(1)$\displaystyle{E:\frac{x^2}{3}+\frac{y^2}{4}=1}$
(2)置 $\displaystyle{x'=\frac{x}{\sqrt{3}},y'=\frac{y}{2}}$
则 $\displaystyle{E}$ 化为单位圆 $\displaystyle{x'^2+y'^2=1}$,且 $\displaystyle{\text{A}'(0,-1)\,,\text{B}'\left(\frac{\sqrt{3}}{2},-\frac{1}{2}\right)\,,\text{P}'\left(\frac{\sqrt{3}}{3},-1\right)}~.$
容易发现 $\displaystyle{\triangle \text{OAB}}$ 为等边三角形 我们猜想 $\displaystyle{\text{HN}}$ 恒过 $\displaystyle{\text{A}}$,故只需证 $\displaystyle{\text{H},\text{N},\text{A}}$ 三点共线,只需证: $$\frac{\text{MN}}{\text{PN}}=\frac{\text{HM}}{\text{AP}}~.$$ 而我们知道 $\displaystyle{\frac{\text{QM}}{\text{PQ}}=\frac{\text{TM}}{\text{AP}}}~,$ 即: $$1-\frac{\text{PM}}{\text{PQ}}=\frac{\text{TM}}{\text{AP}}~.$$ 两式相除,得: $$\frac{1-\frac{\text{MP}}{\text{PQ}}}{\frac{\text{MN}}{\text{PN}}}=\frac{1}{2}~,$$ 即: $$\frac{\text{PN}}{\text{MN}}-\frac{\text{PM}\cdot\text{PN}}{\text{PQ}\cdot\text{MN}}=\frac{1}{2}~.$$ 由切割线定理: $${\text{PM}}\cdot{\text{PN}}=\text{AP}^2=\frac{1}3~.$$ 又: $$\text{PQ}=\frac{\sqrt{3}}{6\cos\angle\text{OPN}}~.$$ 故 $\displaystyle{\text{PN}-\frac{2\sqrt{3}}{3}\cos\angle\text{OPN}=\frac{1}{2}\text{MN}}$,即: $$\text{PN}-\text{OP}\cos\angle\text{OPN}=\frac{1}{2}\text{MN}~.$$ 此式显然
2. 仿射法的定义及性质
定义 1 仿射变换
设椭圆 $\displaystyle{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$,其中 $\displaystyle{a>b>0}$,置变换: $$x'=\frac{x}{a},y'=\frac{y}{b}~.$$ 则椭圆化为单位圆 $\displaystyle{C:x'^2+y'^2=1}~.$
届时,我们可以就可以抛开繁琐的代数计算,运用几何性质解决问题。此前,我们先介绍仿射变换的几个性质。
引理 1
变换后,平面内任意一条直线的斜率变为原来的 $\displaystyle{\frac{a}{b}}~.$
引理 2
变换后,平面上任意区域的面积变为原来的 $\displaystyle{\frac1{ab}}~.$
引理 3
变换后,线段中点依然是线段中点;关于水平线、铅垂线、坐标原点对称的元素依然对称;平面区域的重心保持不变
引理 4
变换前后,平行关系保持不变
引理 5
变换前后,平行线段的长度比保持不变
3. 仿射法导出的常用结论
推论 1
设椭圆 $\displaystyle{\frac{x^2}{a^2}+\frac{y^2}{b^2}}$,直线 $\displaystyle{l}$ 交椭圆于点 $\displaystyle{A}$ 和 $\displaystyle{B}$,点 $\displaystyle{P(x_0,y_0)}$ 为线段 $\displaystyle{AB}$ 的中点,求直线斜率
解:作变换 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为单位圆 $\displaystyle{C:x'^2+y'^2=1}$,且 $\displaystyle{P'\left(\frac{x_0}{a},\frac{y_0}{b}\right)}$
故 $\displaystyle{k_{OP'}=\frac{ay_0}{bx_0}}~.$
由性质 3,$\displaystyle{P'}$ 为 $\displaystyle{A'B'}$ 的中点
在圆中,由垂径定理,$\displaystyle{OP'\bot A'B'}~.$
而 $\displaystyle{k_{A'B'}\cdot k_{OP'}=-1}$,得 $\displaystyle{k_{A'B'}=-\frac{bx_0}{ay_0}}~.$
由上述性质,$\displaystyle{k_l=\frac{b}{a}\cdot k_{A'B'}=-\frac{b^2x_0}{a^2y_0}}~.$
推论 2
设椭圆 $\displaystyle{\Gamma:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)}$,直线 $\displaystyle{l}$ 切椭圆于点 $\displaystyle{P(x_0,y_0)}$,求直线斜率
解:作变换 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为单位圆 $\displaystyle{C:x'^2+y'^2=1}$,$\displaystyle{P'\left(\frac{x_0}{a},\frac{y_0}{b}\right)}~.$
故 $\displaystyle{k_{OP'}=\frac{ay_0}{bx_0}}~.$
在圆中,由切线定理,$\displaystyle{OP'\bot l'}~.$
而 $\displaystyle{k_{l'}\cdot k_{OP'}=-1}$,得 $\displaystyle{k_{l'}=-\frac{bx_0}{ay_0}}~.$
由上述性质 1,$\displaystyle{k_l=\frac{b}{a}\cdot k_{l'}=-\frac{b^2x_0}{a^2y_0}}~.$
推论 3
设椭圆 $\displaystyle{\Gamma:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)}$,$\displaystyle{A}$、$\displaystyle{B}$ 和 $\displaystyle{M}$ 为椭圆上的点,点 $\displaystyle{A}$ 和 $\displaystyle{B}$ 关于原点对称,求证:$\displaystyle{k_{MA}\cdot k_{MB}}$ 为一定值
证明:作变换 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为单位圆 $\displaystyle{C:x'^2+y'^2=1}~.$
则 $\displaystyle{A'B'}$ 为圆 $\displaystyle{C}$ 的直径,所以 $\displaystyle{M'A'\bot M'B'}$,$\displaystyle{k_{M'A'}\cdot k_{M'B'}=-1}~.$
由性质 1,$\displaystyle{k_{MA}\cdot k_{MB}=-1\cdot \frac{b}{a}\cdot \frac{b}{a}=-\frac{b^2}{a^2}}~.$
推论 4
设椭圆 $\displaystyle{\Gamma:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)}$,$\displaystyle{A}$ 和 $\displaystyle{B}$ 为椭圆上的点,点 $\displaystyle{M}$ 为 $\displaystyle{AB}$ 的中点,求证:$\displaystyle{k_{AB}\cdot k_{OM}}$ 为一定值
证明:作变换 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为单位圆 $\displaystyle{C:x'^2+y'^2=1}~.$
由性质 3,$\displaystyle{M'}$ 为 $\displaystyle{A'B'}$ 的中点,由垂径定理,$\displaystyle{O'M'\bot A'B'}$ , $\displaystyle{k_{OM'}\cdot k_{A'B'}=-1}~.$
由性质 1,$\displaystyle{k_{OM}\cdot k_{AB}=-1\cdot \frac{b}{a}\cdot \frac{b}{a}=-\frac{b^2}{a^2}}~.$
推论 5 等角定理
设椭圆 $\displaystyle{\Gamma:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1(a>b>0)}$,$\displaystyle{A}$ 和 $\displaystyle{B}$ 为椭圆上的点,直线 $\displaystyle{AB}$ 交 $\displaystyle{x}$ 轴于点 $\displaystyle{P(x_0,0)}$,在 $\displaystyle{x}$ 轴上求一点 $\displaystyle{G}$,使 $\displaystyle{x}$ 轴平分 $\displaystyle{\angle AGB}$
解:作变换 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为单位圆 $\displaystyle{C:x'^2+y'^2=1}$,$\displaystyle{P'\left(\frac{x_0}{a},0 \right)}~.$
由性质 3,$\displaystyle{\angle A'G'B'}$ 依然被 $\displaystyle{x}$ 轴平分,记 $\displaystyle{B'G'}$ 交圆 $\displaystyle{O}$ 于另一点 $\displaystyle{D'}$
易见 $\displaystyle{\angle A'OG'=\frac{1}{2}\cdot\angle A'OD'=\angle A'B'D'}~.$
又 $\displaystyle{\angle A'P'O=\angle B'P'G'}~,$
所以 $\displaystyle{\angle OA'P'=\angle OG'B'}~.$
又 $\displaystyle{\angle A'G'O=\angle B'G'O}~,$
故 $\displaystyle{\angle OA'B'=\angle A'G'O}~.$
又 $\displaystyle{\angle A'OG'=\angle A'OG'}~,$
故 $\displaystyle{\triangle A'OG'\sim \triangle P'OA'}~.$
进而 $\displaystyle{\frac{OP'}{OA'}=\frac{OA'}{OG'}}~,$
故 $\displaystyle{OP'\cdot OG'=OA'^2=1}~.$
即 $\displaystyle{G'\left(\frac{a}{x_0},0\right)}~.$
由性质 1,$\displaystyle{G\left( \frac{a^2}{x_0},0\right)}~.$
推论 6
过椭圆 $\displaystyle{\Gamma:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$ 上任一点 $\displaystyle{A(x_0,y_0)}$ 作两条倾斜角互补的直线交椭圆于点 $\displaystyle{P}$,$\displaystyle{Q}$,求证:$\displaystyle{k_{PQ}}$ 为一定值
证明:作变换 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为单位圆 $\displaystyle{C:x'^2+y'^2=1}$ , $\displaystyle{A\left(\frac{x_0}{a},\frac{y_0}{b}\right)}~.$
由性质 3,$\displaystyle{A'P'}$,$\displaystyle{A'Q'}$ 仍然关于铅垂线对称,故 $\displaystyle{\angle P'A'B'=\angle OA'B'}~.$
同弧所对的圆周角等于圆心角的一半,故 $\displaystyle{\angle P'OB'=\angle Q'OB'}~.$
又 $\displaystyle{OP'=OQ'}$,等腰三角形三线合一,所以 $\displaystyle{OB'\bot P'Q' }$, $\displaystyle{k_{P'Q'}\cdot k_{OB'}=-1}~.$
又因为 $\displaystyle{k_{OA'}=-k_{OB'}}$ ,所以 $\displaystyle{k_{OA'}\cdot k_{P'Q'}=1~,}$
而 $\displaystyle{k_{OA'}=\frac{a\cdot y_0}{b\cdot x_0}}$ ,因此 $\displaystyle{k_{P'Q'}=\frac{b\cdot x_0}{a\cdot y_0}}~.$
由性质 1,$\displaystyle{k_{PQ}=\frac{b^2\cdot x_0}{a^2 \cdot y_0}}~.$
推论 7
求椭圆 $\displaystyle{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$ 内接三角形的最大面积和外切三角形的最小面积
解:作变换 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为单位圆 $\displaystyle{C:x'^2+y'^2=1}~.$
由琴生不等式: $$S'_{\text{ins}}\leq \frac{3}{2}\cdot \sin\frac{\pi}{3}=\frac{3\sqrt{3}}{4}, S'_{\text{ext}}\geq 3\cot\frac{\pi}{6}=3\sqrt{3}~.$$
由性质 2: $$S_{\text{ins}\max}=\frac{3\sqrt{3}}{4}\cdot ab, S_{\text{ext}\max}=3\sqrt{3}\cdot ab~.$$
推论 8
求以 $\displaystyle{O}$ 为重心的椭圆 $\displaystyle{\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$ 的内接三角形 $\displaystyle{\triangle ABC}$ 的面积
解:作变换 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为单位圆 $\displaystyle{C:x'^2+y'^2=1}~.$
由性质 3,$\displaystyle{O}$ 仍为 $\displaystyle{\triangle A'B'C'}$ 的重心,故 $\displaystyle{\vec{OA'}=\vec{OB'}=\vec{OC'}}$ , $\displaystyle{\triangle A'B'C'}$ 为等边三角形
故 $\displaystyle{S_{\triangle A'B'C'}=\frac{3\sqrt{3}}{4}}$ ,由性质 3,$\displaystyle{S_{\triangle ABC}=\frac{3\sqrt{3}}{4}\cdot ab}~.$
推论 9 软解定理
已知椭圆 $\displaystyle{\Gamma:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$,过 $\displaystyle{T(t,0)}$ 的直线 $\displaystyle{l}$ 交 $\displaystyle{\Gamma}$ 于 $\displaystyle{A}$,$\displaystyle{B}$ 两点,且 $\displaystyle{\frac{AT}{BT}=p}$ ,求 $\displaystyle{l}$ 斜率
解:作变换 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为单位圆 $\displaystyle{C:x'^2+y'^2=1}~.$
由性质 5,仍有 $\displaystyle{\frac{A'T'}{B'T'}=p}$ ,记 $\displaystyle{m=A'T',n=B'T'}$ ,于是 $\displaystyle{\frac{m}{n}=p}~.$
由切割线定理,$\displaystyle{A'T'\cdot B'T'=MT'\cdot NT'}$ ,其中 $\displaystyle{M}$,$\displaystyle{N}$ 为单位圆与 $\displaystyle{x}$ 轴的两交点
即 $\displaystyle{m\cdot n=(1+t')(1-t')=1-t'^2}~.$
接着, $$(m+n)^2=m^2+n^2+2mn=\frac{mn}{\frac{m}{n}}+\frac{mn}{\frac{n}{m}}+2mn=\left(p+\frac{1}{p}+2\right)(1-t'^2)~.$$ 由垂径定理 $$1-\frac{k'^2t'^2}{k'^2+1}=\frac{1}{4}\left(p+\frac{1}{p}+2\right)(1-t'^2)~.$$ 整理,由性质 1 得: $$\frac{1}{1+(\frac{b}{ak})^2}=1-\frac{1}{4}\left(p+\frac{1}{p}+2\right)\left(1-\frac{t}{a}^2\right)~.$$
推论 10
设椭圆 $\displaystyle{\Gamma:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$ ,$\displaystyle{C}$ 为第三象限内椭圆上的一点,$\displaystyle{A}$,$\displaystyle{B}$ 分别是椭圆的上顶点、右顶点,直线 $\displaystyle{OA}$ 与 $\displaystyle{y}$ 轴交于点 $\displaystyle{M}$,直线 $\displaystyle{OB}$ 与 $\displaystyle{x}$ 轴交于点 $\displaystyle{N}$,求证:四边形 $\displaystyle{ABNM}$ 的面积为定值
证明:作变换 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为单位圆 $\displaystyle{O:x'^2+y'^2=1}~.$
于是 $\displaystyle{OM'=\tan{\beta},ON'=\tan{\alpha},\alpha+\beta=\frac{\pi}{4}}~.$
于是 $$ \begin{aligned} S'&=\frac{1}{2}\cdot B'M'\cdot A'N'\\ &=\frac{1}{2}(\tan\alpha+1)(\tan\beta+1)\\ &=\frac{1}{2}\cdot\left[\tan\alpha\tan\beta+(\tan\alpha+\tan\beta)+1\right]\\ &=\frac{1}{2}\cdot[\tan\alpha\tan\beta+1-\tan\alpha\tan\beta+1]\\ &=1 ~. \end{aligned} $$ 由性质 2,$\displaystyle{S=ab}~.$
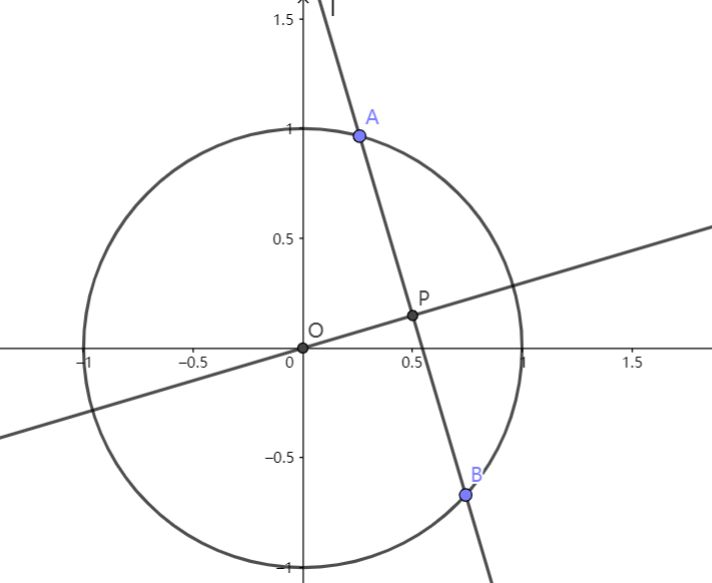
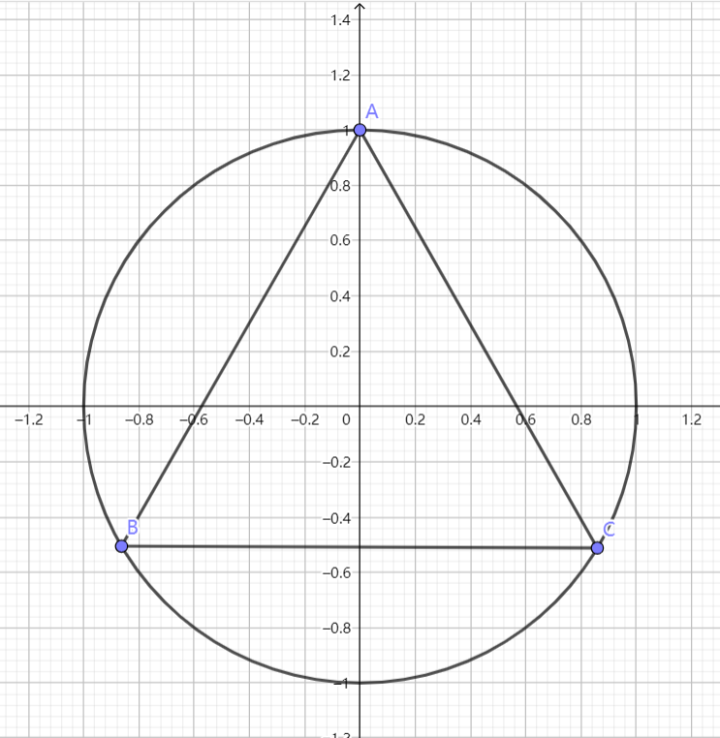
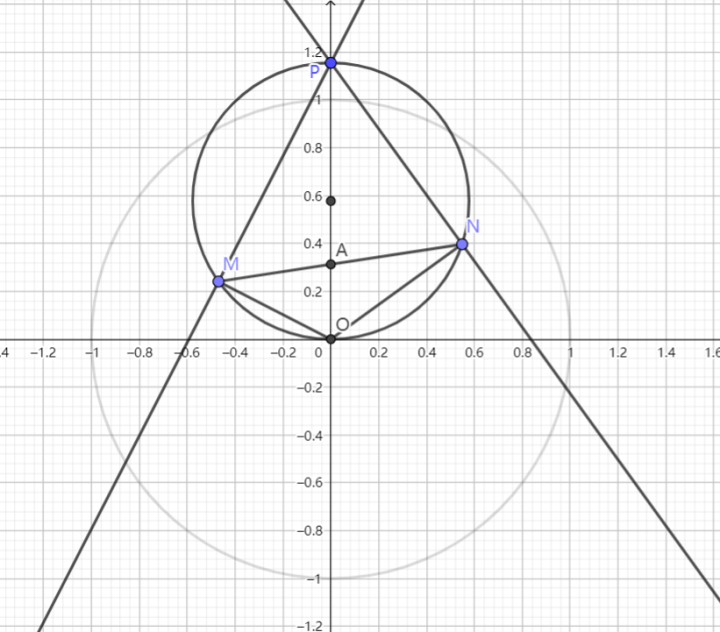
推论 11 蒙日圆
求椭圆 $\displaystyle{\Gamma:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$ 两垂直切线的交点的轨迹方程
解:置 $\displaystyle{x'=\frac{x}{a}\,,y'=\frac{y}b}$,则椭圆化为单位圆 $\displaystyle{x'^2+y'^2=1}~.$
如图,设直线 $\displaystyle{\text{AB}}$,$\displaystyle{\text{AC}}$ 的斜率分别为 $\displaystyle{k_1}$,$\displaystyle{k_2}$,由仿射性质,$\displaystyle{k_1k_2=-\frac{a^2}{b^2}}~.$
设 $\displaystyle{\text{A}(x_0,y_0)}$,于是: $$\text{AB}:y=k_1(x-x_0)+y_0\text{BC}:y=k_2(x-x_0)+y_0 ~.$$
原点到切线的距离为圆的半径,即:$\displaystyle{\frac{|k_{1,2}x_0-y_0|}{\sqrt{k_{1,2}^2+1}}=1}~.$
化简得: $$(x_0^2-1)k_{1,2}^2-2x_0y_0k_{1,2}+y_0^2-1=0~.$$
由韦达定理: $$\frac{y_0^2-1}{x_0^2-1}=-\frac{a^2}{b^2}~.$$
即: $$a^2x_0^2+b^2y_0^2=a^2+b^2~.$$
回代,得: $$\text{M}:x^2+y^2=a^2+b^2~.$$
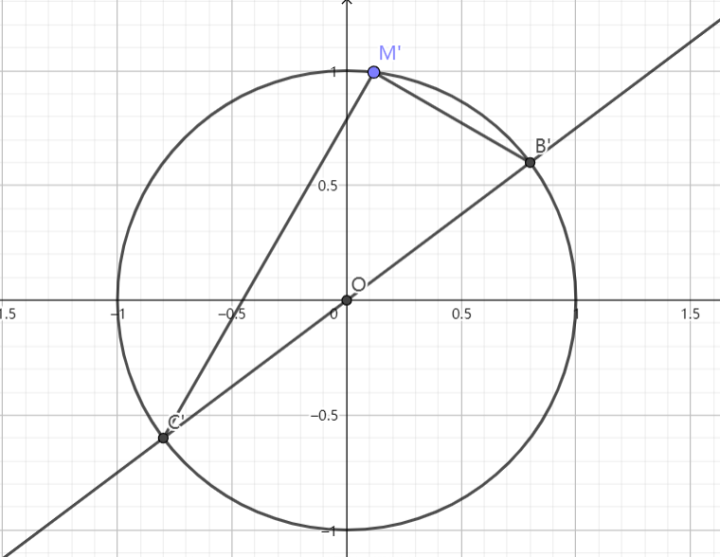
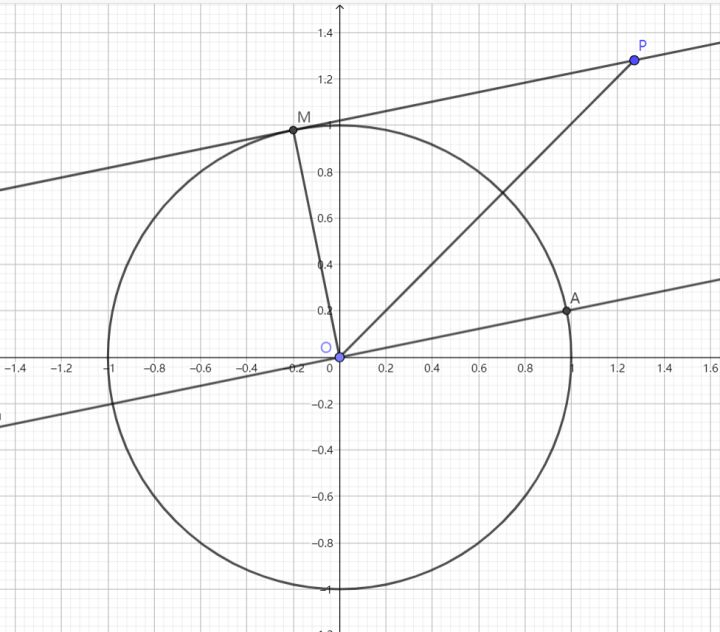
推论 12
设过椭圆 $\displaystyle{\Gamma:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1}$ 外一点 $\displaystyle{P(x_0,y_0)}$ 作椭圆的一条切线 $\displaystyle{l}$ 切椭圆于 $\displaystyle{M}$,连结 $\displaystyle{PM}$,求 $\displaystyle{|PM|}$
解:过 $\displaystyle{O}$ 作直线 $\displaystyle{l'}$ 交椭圆于两点,靠近点 $\displaystyle{P}$ 一侧的点为 $\displaystyle{A}$,设 $\displaystyle{|PM|=\lambda|OA|}$,我们只需要求出 $\displaystyle{\lambda}$ 以及 $\displaystyle{|OA|}$
不妨令 $\displaystyle{x'=\frac{x}{a},y'=\frac{y}{b}}$,则椭圆化为圆 $\displaystyle{C:x'^2+y'^2=1}~.$
变换前后,平行线段比例不变,故 $\displaystyle{\lambda=\frac{|P'M'|}{|OA'|}=\sqrt{\frac{m^2}{a^2}+\frac{n^2}{b^2}-1}}~.$
至于 $\displaystyle{|OA|}$,可以求出切线斜率,与椭圆联立,这里不再赘述
4. 杂例
这里列举一些利用仿射法解决解析几何问题的例子,其中蕴含着该方法的常用技巧
例 1
已知点 $\displaystyle{P\left(t,\frac{1}{2}\right)}$ 在椭圆 $\displaystyle{\Gamma:\frac{x^2}{2}+y^2=1}$ 内,过点 $\displaystyle{P}$ 的直线 $\displaystyle{l}$ 与椭圆 $\displaystyle{\Gamma}$ 相交于 $\displaystyle{A}$ 和 $\displaystyle{B}$ 两点,且点 $\displaystyle{P}$ 是线段 AB 的中点,O 为坐标原点。求 $\displaystyle{S_{\triangle OAB}}$ 的最大值
解:令 $\displaystyle{x'=\frac{x}{\sqrt{2}},y'=y}$,则 $\displaystyle{C:x'^2+y'^2=1}$ ,$\displaystyle{P'\left(\frac{\sqrt{2}}{2}\cdot t,\frac{1}{2}\right)}~.$
$\displaystyle{OP'=\sqrt{\left(\frac{\sqrt{2}}{2}\cdot t\right)^2+{\frac{1}{2}}^2}=\sqrt{\frac{t^2}{2}+\frac{1}{4}}}~.$
由性质 3,$\displaystyle{P'}$ 为 $\displaystyle{A'B'}$ 的中点
由垂径定理,$\displaystyle{OP'\bot A'B'}$ 故 $\displaystyle{A'B'=2\sqrt{1-OP'^2}=2\sqrt{\frac{3}{4}-\frac{t^2}{2}}}~.$
$\displaystyle{S'=\frac{1}{2}\cdot OP' \cdot A'B'=\sqrt{\left(\frac{t^2}{2}+\frac{1}{4}\right)\left(\frac{3}{4}-\frac{t^2}{2}\right)},t\in[-1,1]}~.$
$\displaystyle{S'_{max}=\frac{1}{2}}~.$
由性质 2,$\displaystyle{S_{max}=\frac{\sqrt{2}}{2}}~.$
例 2
已知椭圆 $\displaystyle{\Gamma:\frac{x^2}{b^2}+\frac{y^2}{b^2}=1(a>b>0)}$ 的左焦点为 $\displaystyle{F(-2,0)}$ ,离心率为 $\displaystyle{\frac{\sqrt{6}}{3}}$.
(1)求椭圆 $\displaystyle{\Gamma}$ 的标准方程;
(2)设 $\displaystyle{T}$ 为直线 $\displaystyle{x=-3}$ 上一点,过点 $\displaystyle{F}$ 作 $\displaystyle{TF}$ 的垂线交椭圆于 $\displaystyle{P,Q}$ 两点,当四边形 $\displaystyle{OPTQ}$ 是平行四边形时,求四边形 $\displaystyle{OPTQ}$ 的面积。
解:(1)椭圆的标准方程为 $\displaystyle{\frac{x^2}{6}+\frac{y^2}{2}=1}$
(2)令 $\displaystyle{x'=\frac{x}{\sqrt{6}},y'=\frac{y}{\sqrt{2}}}$,则 $\displaystyle{F'\left(-\frac{2}{\sqrt{6}},0\right) , l':x'=-\frac{3}{\sqrt{6}}}~.$
由性质 4,$\displaystyle{OP'T'Q'}$ 仍为平行四边形,又 $\displaystyle{OP'=OQ'}$ , $\displaystyle{OP'T'Q'}$ 为菱形
故 $\displaystyle{P'Q'\bot OT'}~.$
记 $\displaystyle{l'\bot x}$ 轴于 $\displaystyle{H'}~,$
因为 $\displaystyle{\angle {T'H'O}=\angle {F'BO},\angle T'OH'=\angle T'OH'}~,$
所以 $\displaystyle{\triangle T'OH'\sim\triangle F'BO}~.$
故 $\displaystyle{\frac{OF'}{OT'}=\frac{OB}{OH'}}~,$
得 $\displaystyle{OB=\frac{\sqrt{2}}{2}}~.$
由垂径定理,$\displaystyle{P'Q'=2P'B=2\sqrt{1-OB^2}=\sqrt{2}}~.$
则 $\displaystyle{S_{\text{菱形}OP'T'Q'}=\sqrt{2}\cdot\frac{\sqrt{2}}{2}=1}~.$
由性质 2,$\displaystyle{S_{\text{四边形}OPTQ}=1\cdot \sqrt{6}\cdot\sqrt{2}=2\sqrt{3}}~.$
例 3
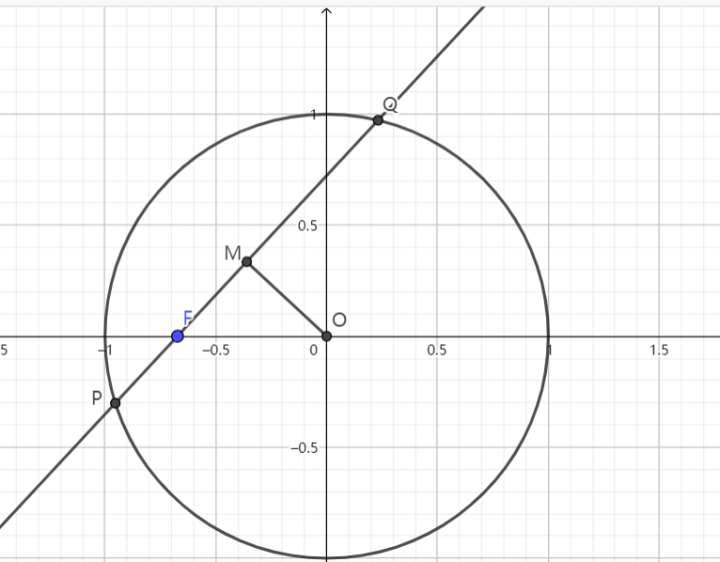
已知椭圆 $\displaystyle{\Gamma:\frac{x^2}{2}+y^2=1}$ ,过左焦点 $\displaystyle{F}$ 的直线 $\displaystyle{l}$ 交椭圆于 $\displaystyle{P,Q}$ 两点,$\displaystyle{M}$ 为 $\displaystyle{PQ}$ 的中点,$\displaystyle{O}$ 为坐标原点。若 $\displaystyle{\triangle FMO}$ 是以 $\displaystyle{OF}$ 为底边的等腰三角形,求直线 $\displaystyle{l}$ 的方程
解:令 $\displaystyle{x'=\frac{x}{\sqrt{2}},y'=y}$,则 $\displaystyle{F'\left(-\frac{1}{\sqrt{2}},0\right)}~.$
由性质 3,$\displaystyle{M'F',OM'}$ 仍旧关于铅垂线对称
在圆中,由垂径定理,$\displaystyle{OM'\bot P'Q'}~.$
故 $\displaystyle{\triangle OM'F'}$ 为等腰直角三角形,$\displaystyle{OF'=\sqrt{2} OM'}~.$
设 $\displaystyle{l':y'=k'\left(x'+\frac{1}{\sqrt{2}}\right)}$ ,于是 $\displaystyle{\frac{1}{\sqrt{2}}=\sqrt{2}\cdot \frac{k'}{\sqrt{2(k'^2+1)}}}~.$
解得 $\displaystyle{k'=1}$ ,由性质 1,$\displaystyle{k=\frac{\sqrt{2}}{2}}~.$
故 $\displaystyle{l:y=\frac{\sqrt{2}}{2}(x+1)}~.$
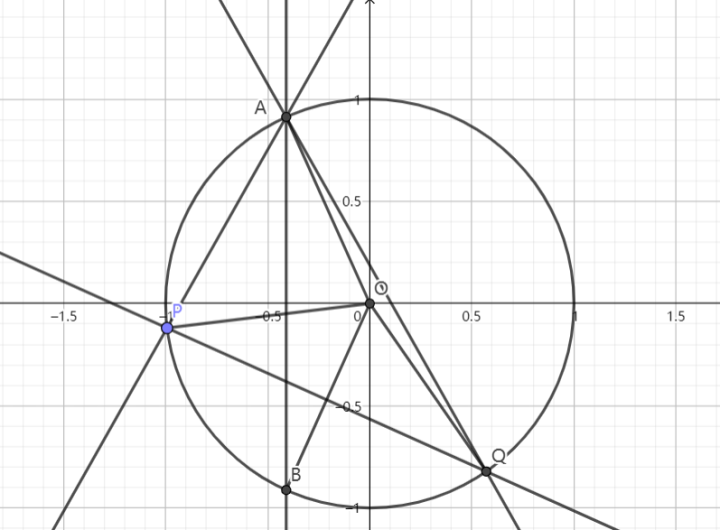
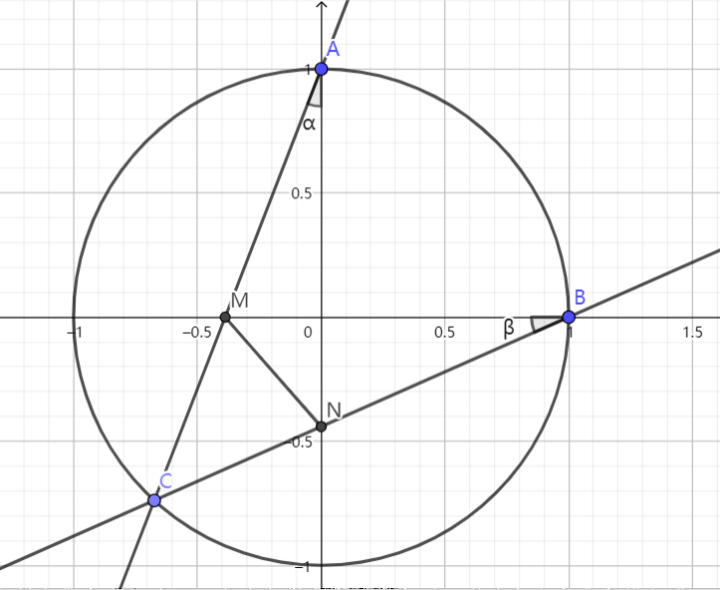
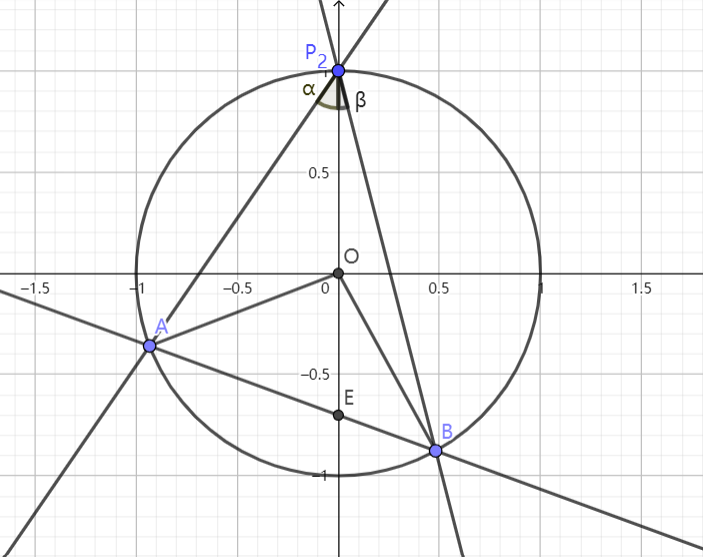
例 4 2017 全国 I 理
已知 $\displaystyle{C:\frac{x^2}4+y^2=1,P_2(0,1)}$,设直线 $\displaystyle{l}$ 不经过 $\displaystyle{P_2}$ 点且与 $\displaystyle{C}$ 相交于 $\displaystyle{A,B}$ 两点,若直线 $\displaystyle{P_2A}$ 与直线 $\displaystyle{P_2B}$ 的斜率之和为 $\displaystyle{-1}$,求证:$\displaystyle{l}$ 过定点
解:作变换 $\displaystyle{x'=\frac{x}{2},y'=y}$ ,则椭圆化为单位圆 $\displaystyle{x'^2+y'^2=1}~.$
记如图所示的 $\displaystyle{\alpha,\beta}$,则 $\displaystyle{A'(\cos2\alpha,\sin2\alpha),B'(\cos2\beta,\cos2\beta)}~.$
$\displaystyle{k_1'=\cot{\alpha},k_2'=\cot{\beta}}$ ,由性质 1,$\displaystyle{k_1'+k_2'=-2}$ ,即 $\displaystyle{\cot{\alpha}+\cot{\beta}=-2}~.$
移项,得 $\displaystyle{\cot\alpha+\cot \beta+2=0}~.$
进而 $\displaystyle{(\cot\alpha+\cot \beta+2)(\cot \alpha+\cot\beta)=0}~.$
展开,得 $\displaystyle{\cot^2\alpha+2\cot\alpha=\cot^2\beta+2\cot\beta}~.$
所以 $\displaystyle{\cot^2\alpha+2\cot\alpha+\frac{1}{2}=\cot^2\beta+2\cot\beta+\frac{1}{2}}~.$
整理,得 $\displaystyle{-\frac{(\tan\alpha+1)^2}{2\tan^2\alpha}=-\frac{(\tan\beta+1)^2}{2\tan^2\beta}}~,$
得 $$\frac{\frac{2\tan\alpha}{1+\tan^2\alpha}+1}{\frac{1-\tan^2\alpha}{1+\tan^2\alpha}-1}=\frac{\frac{2\tan\beta}{1+\tan^2\beta}+1}{\frac{1-\tan^2\beta}{1+\tan^2\beta}-1}~.$$
由万能公式,$\displaystyle{\frac{\sin2\alpha+1}{\cos2\alpha-1}=\frac{\sin2\beta+1}{\cos2\beta-1}}~.$
所以 $\displaystyle{l'}$ 恒过定点 $\displaystyle{(1,-1)}~,$
所以 $\displaystyle{l}$ 恒过定点 $\displaystyle{(2,-1)}~.$
例 5
已知椭圆 $\displaystyle{\Gamma:\frac{x^2}{9}+\frac{y^2}{3}=1}$,过点 $\displaystyle{P(0,2)}$ 作两直线分别交 $\displaystyle{\Gamma}$ 于 $\displaystyle{A,B}$ 和 $\displaystyle{C,D}$ , $\displaystyle{AB,CD}$ 的中点分别为 $\displaystyle{M,N}$,且 $\displaystyle{k_{AB}\cdot k_{CD}=-2}$ ,证明:$\displaystyle{MN}$ 过定点
证明:作变换 $\displaystyle{x'=\frac{x}{3},y'=\frac{y}{\sqrt{3}}}$ ,则椭圆化为单位圆 $\displaystyle{x'^2+y'^2=1}$,$\displaystyle{P'\left(0,\frac{2}{\sqrt{3}}\right)}$
由性质 1,$\displaystyle{k_{A'B'}\cdot k_{C'D'}=-6}~.$
由性质 3,$\displaystyle{M',N'}$ 仍为 $\displaystyle{P'A',P'B'}$ 的中点
由垂径定理,$\displaystyle{OM'\bot P'A',ON'\bot P'B'}~,$
所以 $\displaystyle{O,N',M',P'}$ 四点共圆,则 $$\frac{P'G'}{M'G'}=\frac{N'G'}{OG'}=\frac{P'N'}{OM'}~,$$ $$\frac{P'G'}{N'G'}=\frac{M'G'}{OG'}=\frac{P'M'}{ON'}~.$$
所以 $\displaystyle{\frac{P'G'^2}{OG'^2}=\left(\frac{P'N'\cdot P'M'}{OM'\cdot ON'}\right)^2=\left(k_{A'B'}\cdot k_{C'D'}\right)^2=36}~,$
故 $\displaystyle{\frac{P'G'}{OG'}=6}~.$
又 $\displaystyle{OG'+P'G'=OP'=\frac{2\sqrt{3}}{3}}~,$
故 $\displaystyle{OG'=\frac{2\sqrt{3}}{3}\cdot\frac{1}{7}\,,OG=\frac{2}{7}}~.$
即 $\displaystyle{MN}$ 过定点 $\displaystyle{\left(0,\frac{2}{7}\right)}~.$
5. 习题
习题 1 2019 全国 II 理
已知 $\displaystyle{C:\frac{x^2}4+\frac{y^2}2=1}$,过坐标原点的直线交 $\displaystyle{C}$ 于 $\displaystyle{P,Q}$ 两点,$\displaystyle{P}$ 在第一象限,$\displaystyle{PE\bot x}$ 轴,垂足为 $\displaystyle{E}$,联结 $\displaystyle{QE}$ 并延长交 $\displaystyle{C}$ 于 $\displaystyle{G}$。求证:$\displaystyle{\triangle PQG}$ 是直角三角形
习题 2 2020 全国 I 理
已知椭圆 $\displaystyle{\Gamma:\frac{x^2}{9}+y^2=1}$ , $\displaystyle{A,B}$ 是椭圆的左、右顶点,过直线 $\displaystyle{l:x=6}$ 上一点 P 作 $\displaystyle{PA,PB}$ 分别交椭圆于 $\displaystyle{C,D}$,证明:$\displaystyle{CD}$ 过定点
习题 3
$\displaystyle{P,Q}$ 是椭圆 $\displaystyle{\Gamma:\frac{x^2}{8}+\frac{y^2}{2}=1}$ 上两动点,$\displaystyle{\angle PAQ}$ 的角平分线恒垂直于 $\displaystyle{x}$ 轴,试判断直线 $\displaystyle{PQ}$ 的斜率是否为定值
友情链接: 超理论坛 | ©小时科技 保留一切权利