量子比特

贡献者： certain_pineapple; ASAHI

　　 在经典信息学中，一个比特（bit）代表着一个取值为 0 或者 1 的随机变量。比如一个电容器的状态可以离散表示为一个比特。当电容器处于高电平的时候，我们将其状态记为 1，否则则记为 0。在基于经典物理的信息论中，我们认为 0 和 1 这两种状态是可以被准确无误地区分开的。

　　 在量子信息处理中，量子比特（qubit）是比特这个概念的量子对应。它描述了一个由 $ \left\lvert 0 \right\rangle , \left\lvert 1 \right\rangle $ 表示的二能级量子系统的状态。我们仍然希望两种 “量子状态” 是可以被准确无误地区分开的，这自然要求着 $ \left\langle 0 \middle| 1 \right\rangle =0$。也就是说，$ \left\lvert 0 \right\rangle , \left\lvert 1 \right\rangle $ 张成了一个二维希尔伯特空间。

　　 和经典比特不同的是，量子比特可以处于两种状态的叠加态上。也就是说，一个一般的量子比特可以处在状态

　　 我们目前讨论的全部都是纯态，这相当于是在说，系统的信息已经完全被掌握了（在经典物理中，这代表着系统处于相空间中的一个点）。但是即使我们掌握了系统的全部信息，伴随我们的测量仍然会出现随机性。这也是量子力学和经典世界很不一样的地方。

1. 物理实现

　　 有很多种不同的物理系统都可以实现量子比特。最简单的例子是自旋-1/2 系统，它自然带有一个二维希尔伯特空间。不那么平凡的例子是光子的偏振自由度。虽然光子是自旋-1 的系统，但是因为其没有静止质量，纵波方向的自由度被禁止。因此其偏振只能有两个取值，因此也可以作为量子比特的载体。此外，即使系统有着多于两个能级，比如很多类型的原子和介观量子电路，只要我们只考虑其中的两个能级，并保证有办法确定系统具体处在什么能级上，那么也可以将其作为量子比特的载体。

　　 本部分不会花过多篇幅来讨论实际的物理载体，但是需要强调的是，量子信息科学并不是建立在抽象数学上的空中楼阁，而是有着扎实的物理根基。

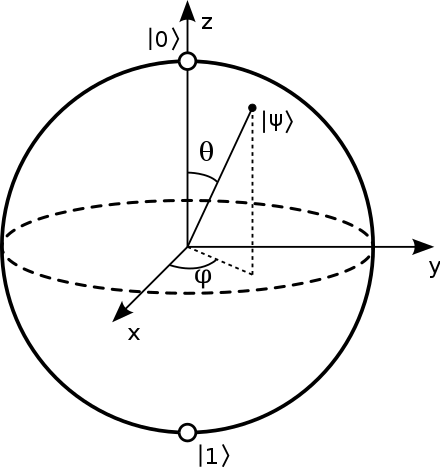
2. 布洛赫（Bloch）球表示

纯态情况

　　 我们来数一数一个量子比特有多少自由的（实数）参数。$a,b$ 各有两个参数，$|a|^2+|b|^2=1$ 构成一个约束条件，看起来有三个约束，但是由于量子态的全局相位可以忽略，因此又会少一个自由度。因此描述一个量子比特只需要两个实数参数就够了。

　　 根据归一化条件，一个一般的量子比特的描述也可以用

　　 由于全局相位 $\alpha$ 并不重要，因此我们总可以使用 $\theta\in[0,\pi]$ 和 $\phi\in[0,2\pi]$ 来表示一个任意的量子态。

　　 可以看到在 Bloch 球表示当中，$\theta$ 和 $\phi$ 刚好就是 Bloch 球上的球坐标。也就是说，任意一个量子比特所处的态都位于 Bloch 球面上。

　　 容易验证，当 Bloch 球上的两个量子态正交时，它们在球面上的点的连线会过球心。这样的点对被称为对径点对。这些点对中最重要的有三对，它们分别对应着 $z,x,y$ 三个坐标轴与球面的交点：

　　 另一个重要的性质是，Bloch 球面上方向 $ \hat{\boldsymbol{\mathbf{n}}} =(\sin\theta\cos\phi,\sin\theta\sin\phi,\cos\theta)$ 所对应的量子态 $\cos\frac{\theta}{2} \left\lvert 0 \right\rangle +\sin\frac{\theta}{2}e^{i\phi} \left\lvert 1 \right\rangle $，刚好是矩阵 $ \hat{\boldsymbol{\mathbf{n}}} \cdot \boldsymbol{\mathbf{\sigma}} $ 本征值为 $+1$ 的本征态。而对径点 $\sin\frac{\theta}{2} \left\lvert 0 \right\rangle -\cos\frac{\theta}{2}e^{i\phi} \left\lvert 1 \right\rangle $ 则是 $ \hat{\boldsymbol{\mathbf{n}}} \cdot \boldsymbol{\mathbf{\sigma}} $ 本征值为 $-1$ 的本征态。这一结论将会在单比特量子门中有重要应用。

混态情况

　　 接下来的部分内，我们将建立了一个自旋 $\frac{1}{2}$ 系统的密度矩阵与 Bloch 球壳及球内的点的一一对应，并且说明Bloch 球壳上的点对应纯态的密度矩阵，而Bloch 球内的点对应混态的密度矩阵，Bloch 球外的点没有与之相对应的密度矩阵。

　　 在真正讨论如何描述混态之前，我们首先重新用密度矩阵的语言描述一下纯态的情况。

　　 上文中提到，Bloch 球面上存在如下对应关系：

　　 运用密度矩阵的知识，也可以很轻易地写出其对应的密度矩阵：

　　 上式中泡利矩阵遵循定义 1 中定义，$\sigma_0$ 表示 $2\times 2$ 的单位阵，$ \boldsymbol{\mathbf{\sigma}} = \left( \sigma_1 ,~\sigma_2,~\sigma_3 \right)$。

　　 上式更好的说明了 Bloch 矢量是如何与一个量子态相对应的。

　　 值得注意的是 Bloch 矢量的分量 $n_a$ 也是有物理意义的，它恰好是所对应的泡利矩阵的期望：

　　 上式运算中遵循爱因斯坦求和约定，最后一步运用了泡利矩阵迹为 $0$ 的性质，同时运算中使用了泡利矩阵之间的乘积公式式 6 。

　　 下面让我们的目光回到一般的密度矩阵上，我们知道，对于一个任意的 $2\times 2$ 厄米矩阵，可以写成以下形式：

　　 其中，$m_1,~m_2,~a,~b$ 都为实数。可见所有 $2\times 2$ 厄米矩阵厄米矩阵都可以写成泡利矩阵和的形式，也就是密度矩阵可写成上边的形式。

　　 考虑密度矩阵的迹为 $1$，而泡利矩阵 $\sigma_1$，$\sigma_2$，$\sigma_3$ 迹为 0，所以密度矩阵所对应 $\frac{m_1+m_2}{2}$ 应为 $\frac{1}{2}$，则：

　　 上式中的 $ \boldsymbol{\mathbf{n}} $ 即使密度矩阵对应的 Bloch。由于密度矩阵的半正定性，应当有 $ \operatorname {det}\rho \geqslant 0$，则：

　　 上式当且仅当 $ \operatorname {det} \rho = 0 $ 时取等号，$ \operatorname {det}\rho = 0$ 意味着 $\rho$ 仅有一个为 $1$ 的本征值，也就是纯态，那么可以说，当且仅当密度矩阵描述的是一个纯态时，所对应的 $ \left\lvert \boldsymbol{\mathbf{n}} \right\rvert ^2 = 1$。混态时，$ \left\lvert \boldsymbol{\mathbf{n}} \right\rvert ^2\leqslant 1$，也就是对应的 Bloch 矢量在 Bloch 球内部。由此，我们给出了一个密度矩阵如何唯一对应一个 Bloch 矢量，同时，任意一个 Bloch 球内部的矢量也可以唯一对应一个密度矩阵，方法是用其在直角坐标系下的三个坐标代替上文中 $n_1,~n_2,~n_3$。球外的点因为 $ \left\lvert \boldsymbol{\mathbf{n}} \right\rvert ^2\geqslant1$ 所以没有与之相对应的密度矩阵。

　　 这样定义出来的混态的 Bloch 矢量有意义吗？答案是有的，因为我们式 6 推导出来的 Bloch 矢量相关的性质并没有依赖 $ \left\lvert \boldsymbol{\mathbf{n}} \right\rvert ^2 = 1$。

　　 特别的，密度矩阵为 $2\times 2$ 单位矩阵的量子态所对应的 Bloch 矢量为零矢量。

　　 综上所述，我们建立了一个自旋 $\frac{1}{2}$ 系统的密度矩阵与 Bloch 球壳及球内的点的一一对应，并且说明了球壳上的点对应纯态的密度矩阵，而球内的点对应混态的密度矩阵，球外的点没有与之相对应的密度矩阵。

3. 高维量子比特

　　 如果不加说明，量子比特都指代的是包含两个能级的量子系统的状态，不过在一些特殊情况下，我们也可以考虑更加高维的量子比特。为了做到这点只需要将希尔伯特空间的维度推广到 $d$ 维。

　　 当 $d=3$ 时，我们称此时的量子比特为 qutrit，在 $d$ 为任意大于等于 2 的正数时，我们称此时的量子比特为 qudit。

4. 多个量子比特

　　 单个量子比特构成了量子信息的基本单元。在更加一般的量子信息处理任务中，我们往往需要处理 $n$ 个不同的量子比特。复合系统的原理告诉我们，如果系统由两个子系统 $A,B$ 所构成，那么这个系统的希尔伯特空间由子系统希尔伯特空间的张量积 $\mathcal{H}_{AB}=\mathcal{H}_A\otimes\mathcal{H}_B$ 描述。这保证了我们可以合理地描述多个量子比特的量子态。

　　 如果系统含有 $n$ 个量子比特，并且记录第 $k$ 个量子比特对应的系统的基矢为 $\{ \left\lvert 0 \right\rangle _k, \left\lvert 1 \right\rangle _k\}$，那么¹$$ |\psi\rangle=\sum_{j_1, j_2, \ldots, j_n \in\{0,1\}} \alpha_{j_1 j_2 \ldots j_n}\left|j_1\right\rangle_1 \otimes\left|j_2\right\rangle_2 \otimes \cdots \otimes\left|j_n\right\rangle_n~, $$其中 $\alpha_{j_1j_2\ldots j_n}$ 是复数而且满足归一化条件 $\sum_{j_1j_2\ldots j_n}|a_{j_1j_2\ldots j_n}|^2=1$。

　　 在不引起歧义的情况下，我们往往会将多比特空间的基矢量简记为$$\left|j_1\right\rangle_1 \otimes\left|j_2\right\rangle_2 \otimes \cdots \otimes\left|j_n\right\rangle_n\to \left\lvert j_1j_2\ldots j_n \right\rangle ~. $$

　　 张量积的一个重要特性是：$\mathcal{H}_{AB}$ 中的态 $ \left\lvert \psi \right\rangle _{AB}$ 不一定能够写作 $\mathcal{H}_A$ 和 $\mathcal{H}_B$ 中的态的张量积。如果一个两比特纯态满足这个性质，那么我们称这个态是两比特纠缠态。

　　 纠缠在信息的角度代表着不平凡的量子关联，在后面的章节中我们将会详细地讨论这件事情。

1. ^ 这里用到了一个隐含假设，那就是每个量子比特对应的系统都是可编号、可区分的。这并不与量子力学中的全同性假设矛盾。比如在定域系统等体系中，我们仍然可以对不同的量子模式进行区分。