贡献者: addis
预备知识 高中立体几何
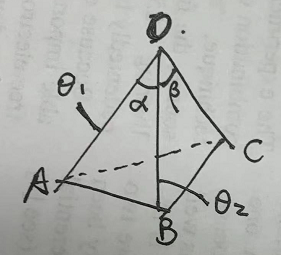
图 1:(左图)已知 $\theta_1$,$\theta_2$ 和 $\phi$ 求 $\alpha$;(右图)已知 $\theta$ 和 $\phi$ 求 $\gamma$
我们考虑如图 1 中三棱锥顶点 $O$ 处的 3 条棱和 3 个面之间的角度关系。这里涉及了三种角:两条棱之间的夹角(线线角)$\theta$,棱和面的夹角(线面角)$\gamma$,以及面和面的夹角(面面角)$\phi$。对给定的顶点,每种角都有各有 3 个,共 9 个。我们先不讨论底面 $ABC$ 的位置如何,如果顶点的三条棱的方向都确定,我们就说顶点的形状确定。
显然,我们无需知道所有 9 个角的大小才能确定顶点的形状。这里给出一个类似于三角形余弦定理的公式,将线线角和面面角联系起来。线线角可以类比余弦定理中的边长,面面角类比余弦定理中的夹角。
\begin{equation}
\cos\alpha = \cos\theta_1 \cos\theta_2 + \sin\theta_1 \sin\theta_2 \cos\phi~.
\end{equation}
如果已知该式中的 4 个角中的 3 个,就可以求出另一个角。与余弦定理类似,在求解 $\theta_1$ 或 $\theta_2$ 时可能存在两个解,也可能无解。注意如果我们交换 $\theta_1$ 和 $\theta_2$ 的值,上式仍然满足(这相当于创造一个镜像三棱锥)。
一个关于线面角的常用公式是
\begin{equation}
\sin\gamma = \sin\phi\sin\theta_1~,
\end{equation}
其中 $\gamma$ 是线段 $OB$ 和三角形 $OAC$ 的线面角。虽然乍看之下从该式无法判断出 $\gamma$ 是钝角还是锐角,但仔细分析可以发现若 $\phi$ 为钝角 $\gamma$ 也一定是钝角。
例 1 已知三个线线角求线面角
若已知 $\theta_1$,$\theta_2$ 和 $\alpha$,则
\begin{equation}
\cos\phi = \frac{\cos\alpha - \cos\theta_1 \cos\theta_2}{\sin\theta_1 \sin\theta_2}~.
\end{equation}
例 2
未完成:图
若一个正方形,一个正五边形,一个正六边形拼在一起,求正方形和正五边形的共同边与正六边形所成的线面角。
利用式 1 , 令正方形的内角为 $\theta_1 = \pi/2$,六边形的内角为 $\theta_2 = 2\pi/3$, 五边形的内角为 $\alpha = 3\pi/5$,代入式 1 解得正方形与六边形的二面角为 $\phi$ 为
\begin{equation}
\phi = \arccos\frac{\cos\alpha - \cos\theta_1 \cos\theta_2}{\sin\theta_1\sin\theta_2} \approx 1.936 \,\mathrm{rad} \approx 110.9^\circ~,
\end{equation}
再代入式 2 ,$\phi$ 是钝角,所以 $\gamma$ 也是钝角,所以
\begin{equation}
\gamma = \pi - \arcsin\left(\sin\phi \sin\theta_1\right) \approx 1.9357 \,\mathrm{rad} \approx 110.9^\circ~.
\end{equation}
这与 $\phi$ 相同,这是因为我们有一个正方形。
角边角
事实上解三棱锥顶角和解三角形类似,面面角可以看作三角形的 “角”,而两条棱之间的角可以看作三角形的 “边”。例如式 1 就可以看作 “边角边” 问题(已知 $\theta_1, \phi, \theta_2$)求第三边 $\alpha$。
那么我们再来看若已知 “角边角”($\theta_1, \alpha, \theta_2$)求下一边 $\beta$(图 2 )
图 2:角边角问题
$\beta$ 满足
\begin{equation}
(C_1^2 - S_\alpha^2 C_1^2 C_2^2 - C_\alpha^2 C_2^2)T_\beta^2 + 2S_\alpha C_\alpha S_1^2 C_2 T_\beta - S_1^2 S_\alpha^2 = 0~,
\end{equation}
其中 $C,S,T$ 分别代表 $\cos, \sin, \tan$,$C_1 = \cos\theta_1, C_2 = \cos\theta_2$。该式子可以直接使用两次 “边角边” 公式解出来。注意上式若存在两个解,必须剔除一个无意义的解。
1. 证明
我们可以用球坐标系来证明式 1 。令极坐标 $(\theta_1, \phi_1)$ 和 $(\theta_2, \phi_2)$ 代表的两个单位矢量的坐标分别为
\begin{equation}
(\sin\theta_1\cos\phi_1, \sin\theta_1\sin\phi_1, \cos\theta_1)~,
\qquad
(\sin\theta_2\cos\phi_2, \sin\theta_2\sin\phi_2, \cos\theta_2)~,
\end{equation}
\begin{equation}
\cos\alpha = \cos\theta_1 \cos\theta_2 + \sin\theta_1 \sin\theta_2 \cos\left(\phi_2 - \phi_1\right) ~.
\end{equation}
证毕。
再来证明式 2 ,我们仍然使用球坐标,将射线 OA 作为极轴,面 OAC 为 $xz$ 平面,线面角中 “线” 的极坐标为 $(1, \theta, \phi)$,该点的 $y$ 坐标为 $\sin\theta \sin\phi$ 而 $y = \sin\gamma$,所以 $\sin\gamma = \sin\theta \sin\phi$。证毕。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。