相移

贡献者： Zona; addis

　　 当光线以不同入射角入射时，振幅反射系数 $r$ 与振幅透射系数 $t$ 可能出现负数情形，其负号的物理意义为电场 $\mathbf{E}$ 的相应分量反向，相当于发生 $\pi$ 弧度的相移。相移在光的干涉与衍射中有重要影响。 下面我们分情况讨论相移：

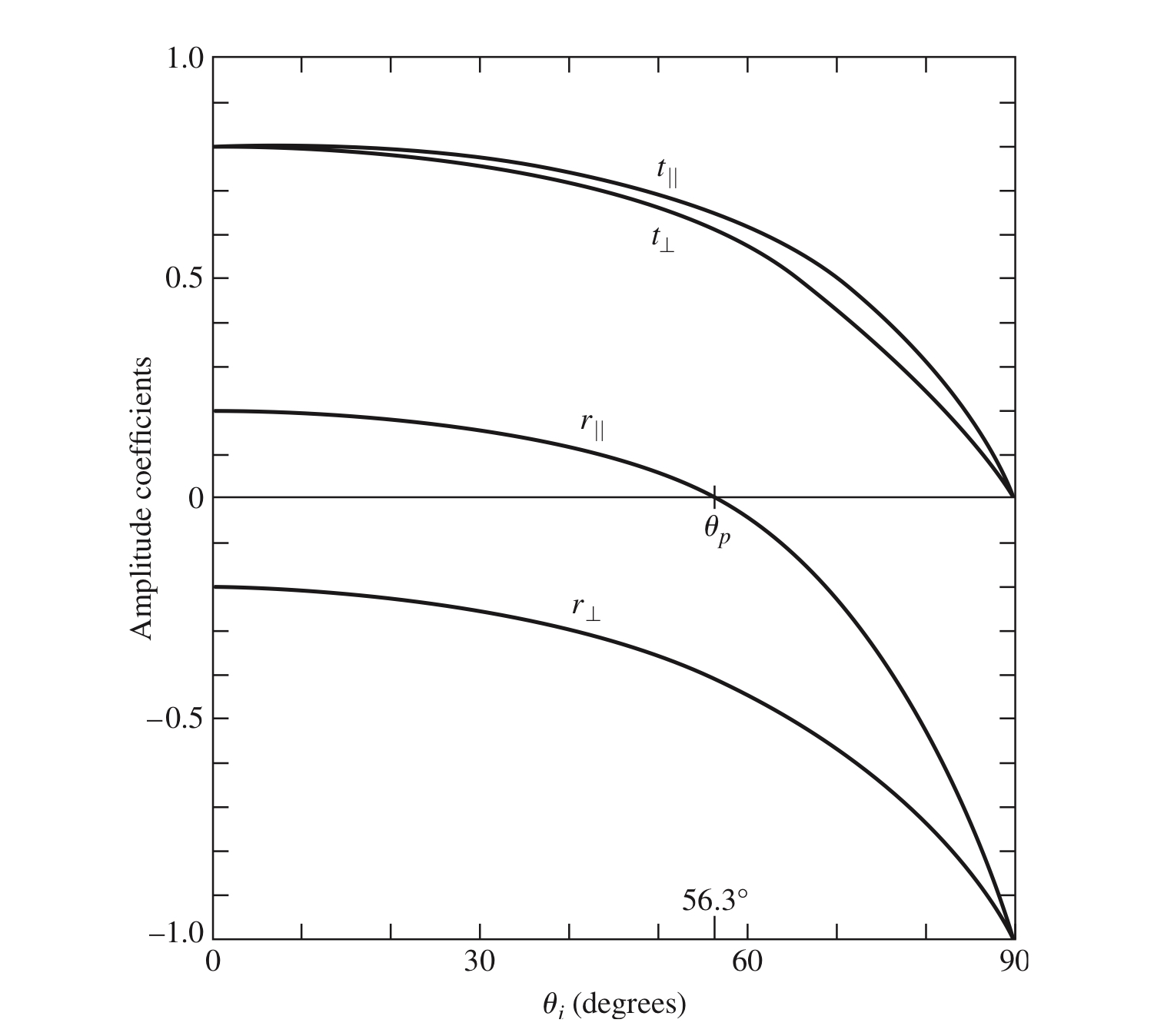
　　 1. 若 $\mathbf{E}$ 平行于入射面，令 $$r_p={\displaystyle \frac{n_2\cos {\theta }_i-n_1\cos {\theta }_t}{n_1\cos {\theta }_t+n_2\cos {\theta }_i}}<0.$$ 化简得 $$\sin ({\theta }_i-{\theta }_t)\cos ({\theta }_i+{\theta }_t)>0.$$

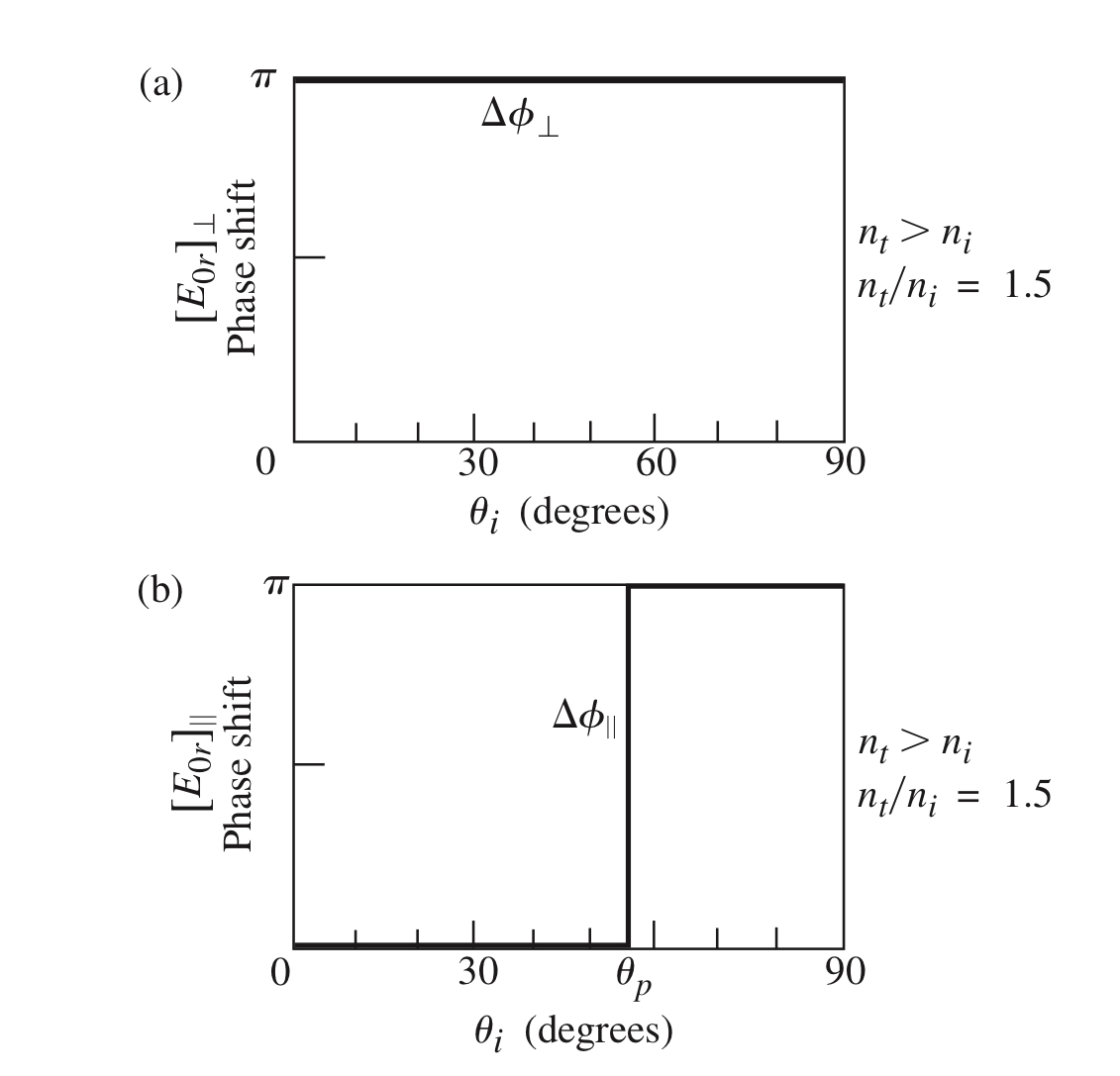
　　 对于外反射情形，$n_t>n_i\Rightarrow {\theta }_i>{\theta }_t$，则 $${\theta }_i+{\theta }_t>\frac{\pi }{2}.$$ 以 ${\theta }_i+{\theta }_t=\pi /2$ 为界，由于 ${\theta }_i\propto {\theta }_t$，则当 ${\theta }_i>{\theta }_B$ 时，${\theta }_i+{\theta }_t>\pi /2$。也即，当入射角大于布儒斯特角时，电场的平行分量发生 $\pi$ 弧度的相移。

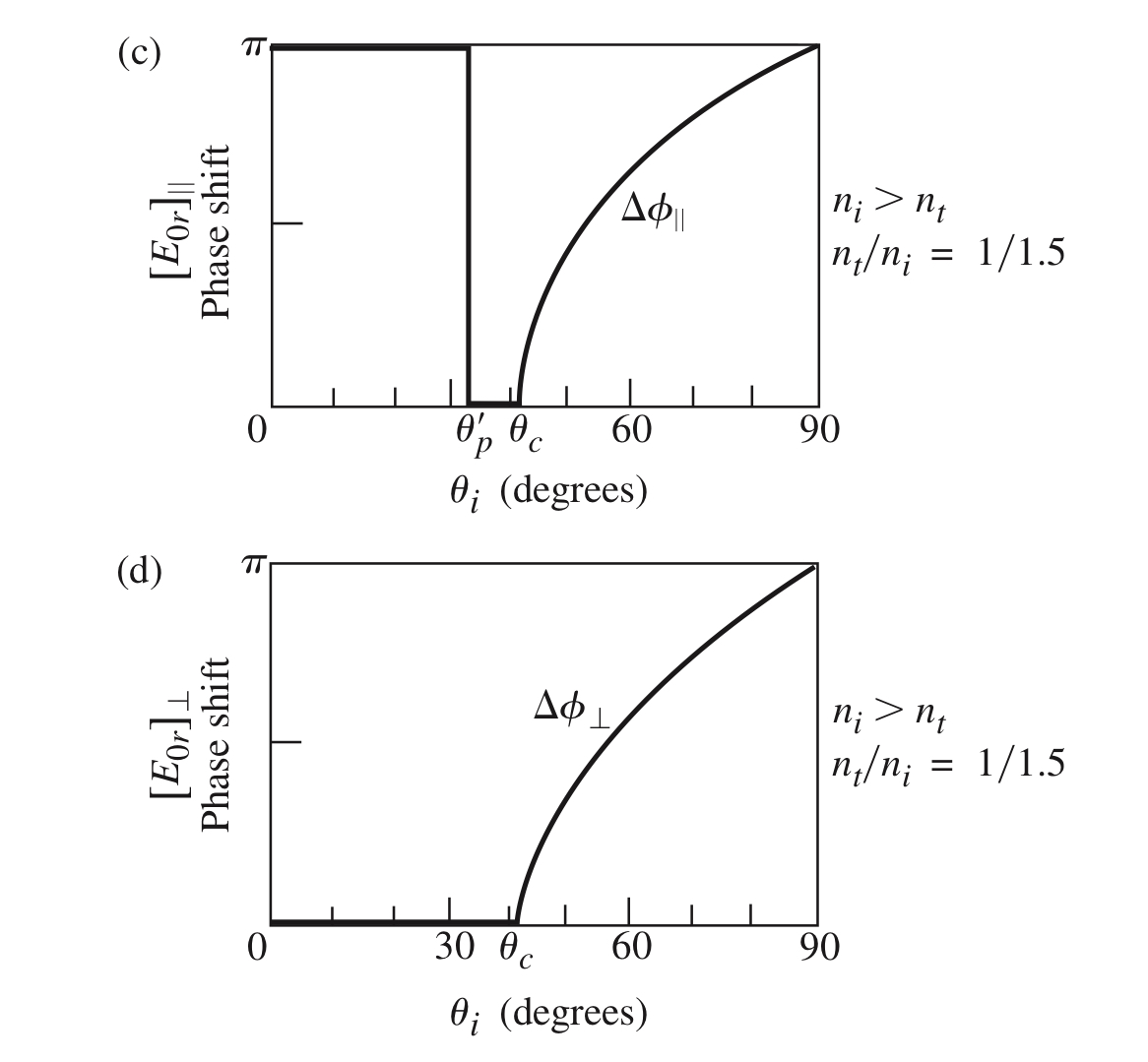
　　 对于内反射情形，$n_t<n_i\Rightarrow {\theta }_i<{\theta }_t$，则 $${\theta }_i+{\theta }_t<\frac{\pi }{}.2.$$ 同理可得，当入射角小于布儒斯特角时，电场的平行分量发生 $\pi$ 弧度的相移。

　　 2. 若 $\mathbf{E}$ 垂直于入射面，令 $$r_s=\frac{n_1\cos {\theta }_i-n_2\cos {\theta }_t}{n_1\cos {\theta }_i+n_2\cos {\theta }_t}<0,$$ 化简得 $$\sin ({\theta }_t-{\theta }_i)<0.$$ 同理可知，对于外反射，电场垂直分量相移恒为 $\pi$；对于内反射，入射角小于临界角 ${\theta }_c$ 时，相移恒为 0。

　　 3. 我们并没有讨论 $t_s$ 和 $t_p$ 与入射角关系，是由于无论入射角取何值，$t$ 恒大于 0。

　　 内反射： $r$、$t$ 作为入射角的函数（同图 1 ）

　　 综上所述，在考虑一般的问题时，我们可以使用以下口诀来判断电场分量所发生的相移： 外直内平相差 $\pi$。 意思是，当 $n_t>n_i$ 时，电场的垂直分量有相移 $\pi$；当 $n_t<n_i$ 时，电场的平行分量有相移 $\pi$。