贡献者: addis; Connection; JierPeter; Giacomo; 欄、停敘
微积分的核心概念是极限(Limit),常见的极限有数列的极限,函数的极限等。数列是离散的,比较容易理解。事实上,数列就是一种特殊的函数(定义域为 $N^{*}$)。
我们通过一些例子引入。
例 1 圆周率
我们知道 $\pi$ 是一个无理数,所以 $\pi$ 的小数部分是无限多的。目前用计算机已经可以将 $\pi$ 精确地计算到小数点后数亿位。然而在实际应用中,往往只用取前几位小数的近似即可。下面给出一个数列,定义第 $n$ 项是 $\pi$ 的前 $n$ 位小数近似(去尾),即
\begin{equation}
a_0 = 3,\,\, a_1 = 3.1,\,\, a_2 = 3.14,\,\, a_3 = 3.141,\,\dots~
\end{equation}
显而易见,当 $n$ 趋于无穷时,$a_n$ 趋于 $\pi$。无穷(Infinity)用符号 $\infty$ 来表示。我们说该数列的极限值是 $\pi$,也可以简称极限(Limit)。以上这种情况,用极限符号表示,就是
\begin{equation}
\lim_{n \to \infty } {a_n} = \pi ~.
\end{equation}
这里 $\lim$ 是极限的数学符号,下方用箭头表示某个量 “无止境” 变化的过程。对于数列而言,唯一的 “无止境” 变化就是项标 $n$ 不断增加。
$\lim\limits_{n \to \infty }$ 在这里相当于一个 “操作”,叫做算符(operator)。它作用在整个数列上,并输出一个数,也就是数列的极限值。这有些类似于函数输入一个自变量并输出一个函数值,只不过 $\lim$ 算符的自变量从数换成了数列。所以不要误以为式 2 是说当 $n = \infty$ 时,有1 $a_n=\pi$,而要理解成数列 $a_n$ 经过算符 $\lim\limits_{n \to \infty }$ 的作用以后,得出的结果是 $\pi$。类比函数 $\sin x = y$,是说 $x$ 经过正弦函数作用后等于 $y$。所以从概念上来说,极限中的 “趋于” 和 “等于” 是不同的。趋于是数列整体的性质,而不是某一个项的性质。
我们可以总结出以上数列的一个性质,并把它作为数列极限的一般定义。具有极限的数列最显著的特征是,随着 $n$ 增加,后面的所有项都越来越接近极限值。可是一个难点在于如何定义 “越来越接近”。先看一个错误的理解:考虑数列
\begin{equation}
a_1 = 3.21,\ a_2 = 3.201,\ a_3 = 3.2001,\ a_4 = 3.20001, \dots~
\end{equation}
这个数列也同样越来越接近 $\pi$,但直觉告诉我们,它的极限是 $3.2$ 而不是 $\pi$。
既然要讨论有多接近,那就要引入距离。我们可以把第 $a_n$ 和极限值 $\pi$ 的距离用绝对值定义为 $ \left\lvert a_n - \pi \right\rvert $。对式 1 的数列,可以发现这个距离不光是越来越小,而且想要多小就有多小。例如要求 $ \left\lvert a_n - \pi \right\rvert < 10^{-2}$,容易发现 $n > 1$ 时就总能满足;又例如要求 $ \left\lvert a_n - \pi \right\rvert < 10^{-10}$,容易发现 $n > 9$ 时就总能满足;一般地如果要求 $ \left\lvert a_n - \pi \right\rvert < 10^{-q}$($q$ 为整数),只要 $n > q-1$ 就总能满足,这就意味着 $\lim\limits_{n \to \infty } a_n = \pi$。
有了这个定义,我们就可以轻易地判断式 3 的极限不是 $\pi$。因为无论 $n$ 为多大,总是有 $ \left\lvert a_n - \pi \right\rvert > 3.2 - \pi > 0.05$,所以如果要求一个比这更小的距离,那么就没有任何 $n$ 可以满足。
定义 1 数列的极限
考虑无穷项的实数数列 $a_1, a_2, \dots$,若存在一个实数 $A$,使得:无论多么小的正数 $\varepsilon$,总存在正整数 $N$,对任意 $n > N$ 都满足 $ \left\lvert a_n - A \right\rvert < \varepsilon$,则该数列的极限就是 $A$。
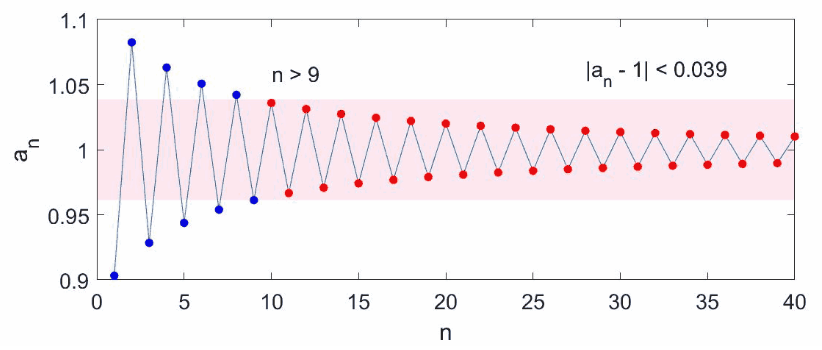
图 1:数列的极限(
查看动画):图中每点代表数列的一项,数列的极限值为 $1$,红色区域表示对距离 $ \left\lvert a_n - A \right\rvert $ 的要求,满足要求的 $a_n$ 为红色,不满足的为蓝色。无论红色区域有多窄(只要不为零),总能找到一个不等式 $n > N$ 使之后所有的点都是红色。
我们来看几个简单的例题,加深一下印象。
例 2 根据定义证明对数列 $\displaystyle a_n= {(-1)^n}{1\over{2^n}}$,$\lim\limits_{n\to\infty}a_n=0$
证明:
对任意 $\varepsilon$,取 $N=[-\log_2\varepsilon]$,则 $n>N$ 时有
$n>-\log_2\varepsilon$,即 $2^{-n}<\varepsilon$。又 $|a_n-0|=2^{-n}$。
因此,对任意 $\varepsilon$,存在 $N=[-\log_2\varepsilon]$,使得当 $n>N$ 时,$|a_n-0|<\varepsilon$。根据定义有 $\lim\limits_{n\to\infty}a_n=0$。
一些数列不存在极限:
习题 1
考虑数列 $a_n = n$ 以及 $a_n=(-1)^n$。它们存在极限吗?
定义 2 数列的敛散性
如果一个数列不存在极限,就称它是发散(divergent)的。如果存在极限,则称它是收敛(convergent)的。
例 3
容易发现数列的极限和前面有限项的值都无关,例如把式 1 中的前 10 项都改成 $0$,那么该数列的极限仍然是 $\pi$。把前一万项改成 $0$ 也同理。
例 4
根据定义,数列极限也并不要求 $n\to \infty$ 时数列的项不能等于极限值,例如数列
\begin{equation}
b_0 = 3.3~,\,\, b_1 = 3.2~, \,\, b_2 = \pi~, \,\, b_3 = \pi~, \,\, b_n = \pi \;\; (n \ge 2)~.
\end{equation}
当 $n \ge 2$ 时所有的项都等于 $\pi$,那么根据
定义 1 他的极限显然也是 $\pi$。因为令 $n > 1$ 即可满足定义中对距离的任何限制。
例 5
注意存在极限的数列未必要求距离 $ \left\lvert a_n - A \right\rvert $ 是严格递减的,例如数列
\begin{equation}
\frac{1}{2},\;\; \frac{1}{4},\;\; \frac{1}{3},\;\; \frac{1}{5},\;\; \frac{1}{4},\;\; \frac{1}{6},\;\; \frac{1}{5},\;\; \frac{1}{7},\;\; \dots~
\end{equation}
的极限是 $0$。
1. ^ 有两个理由可以说明这种理解不正确:首先,按定义,每个 $a_n$ 都是有理数,而 $\pi$ 是无理数,所以不应该有任何一个 $a_n=\pi$;其次,$\infty$ 不是一个实数,不存在 $n=\infty$ 的说法。这里的 $n\to\infty$ 只是表示 $n$ 无限增加的过程。
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。