弧度制与任意角（高中）

                     

贡献者： 欄、停敘; jingyuan; addis; Giacomo

　　 任意角和弧度制在高中数学中属于基础概念。类似于 “实数”，尽管在后续课程中起着重要作用，但许多教材在讲解时往往只是定义角的正负方向，并给出它们与坐标系的关系，而缺乏直观的动机和背景，使得学生在初学时难以理解其意义。而关于弧度制，传统教科书在介绍时，通常直接抛出弧度与角度之间的转化公式，而没有详细解释引入弧度制的必要性，这让许多人在初次接触弧度制时感到困惑：“为什么需要弧度制？”。另外，日常生活中以 “度” 作为单位描述角度早已深入人心，且这些角度通常是简单的整数，而弧度值却常以分数乘以 $\pi$ 的形式出现，其表达的复杂性在视觉上与角度形成了鲜明对比，这进一步加剧了初学者对弧度制的抗拒心理。

　　 本文针对这些问题进行补充，不仅介绍弧度制和任意角的定义，还会探讨它们的必要性和直观理解，使读者不会有 “空降知识” 的感觉，而是能够循序渐进地理解这些概念为何被引入，以及它们如何在数学中发挥作用。另外需要注意，尽管二者通常放在一起学习，但弧度制和任意角并不必然关联。

1. 为什么采用弧度制？

　　 在日常生活中，角的使用主要集中在两种情境：一是描述两条直线之间的倾斜关系，二是通过圆心角来分割圆周。在表达倾斜的角度时，“度分秒” 系统十分方便，它精细且规整，足以满足日常使用的需求。对于圆的分割，由于这一操作在人们的生活中极为常见，通常并不需要精确量取角度值，因而人们往往忽略了这种分割实际上依赖于角度的概念。

　　 早在约公元前 2000 年，古巴比伦人选择用 $360^\circ$ 来表示圆周的完整度量，这一选择可能与 360 的独特性质有关——360 是最小的、能够被除 7 以外所有一位数整除的整数。这一性质使得 $360^\circ$ 在处理常见的 “将圆分成几份” 的问题时极为便利，既能满足分割的精细需求，又避免了度量数值过大而难以操作的问题。但这种基于便利性的选择，并不具有数学上的普遍性。例如，有人可能主张，为了使圆能够被分成 7 等份且每一份的度数为整数，可以采用 $2520^\circ$ 作为圆周的度量。这样的选择在理论上完全可行。此外，刚接触度分秒的初中生可能会感到困惑：既然现代社会普及了十进制，为何仍然沿用六十进制的度分秒？他们或许会想，若直接将圆周设定为 $100^\circ$，不是更简单直观吗？这种随意性与英制单位、市制单位，甚至曾经的某些公制单位类似，它们都是根据人们的习惯和实际需求设定的。

　　 然而，在数学领域，这种依赖习惯的单位定义可能会带来问题。数学需要一种普适且逻辑严密的方式来定义角的度量，以避免随意性，同时在各种情境下保持简洁。此外，数学计算通常涉及无单位的纯数字，而非带有单位的量，由此问题在公元 6 世纪时被印度数学家阿耶波多（Aryabhata）发现。他在研究正弦函数时遇到了一个不知如何处理的情况¹：

其中，$\sin 30^\circ$ 是一个无单位的实数，而 $60^\circ$ 则是一个带有角度单位的量。这种单位的不一致使得它们无法直接进行代数运算（例如加法或乘法），类似于 “$1\text{元} + 2$”，使人无法理解结果的意义。此外，随着数学研究的深入，人们还需要计算角 $\alpha$ 的平方、立方等幂次以及它们的和。如果继续使用 “度” 为单位，这将引入诸如 $\circ^2$ 和 $\circ^3$ 等奇怪的单位。这些实际需求促使数学家思考如何定义一种新的角度度量方式，以满足以下要求：

1. 能够将角度转化为无单位的量，或者单位是 “1” 的量，从而便于代数运算。
2. 与传统的 “度分秒” 系统具有明确的换算关系。
3. 定义应独立于历史、习惯，具有普适性和数学上的严密性，并能在复杂分析、物理学等领域中表现出自然的适用性。

　　 在这个问题被发现之前，人们已经有了分割圆的经验。由于生活中容易量取长度，人们常将角度的分割转化为长度的分割，从而降低测量的难度。尽管，现在人们知道圆周的长度通常是一个无理数，这种方法事实上也是一种近似。然而，这一思路为角度测量问题的解决提供了重要启发。

　　 阿耶波多通过选择用同一单位度量圆的半径和圆周，实际上提出了一个与现代弧度制几乎一致的概念。1748 年，瑞士数学家欧拉（Euler）在其著作《无穷小分析概论（Introduction to the Analysis of the Infinite）》中，正式定义了以圆的半径作为弧长的度量单位。下面看看这样的定义可以推知些什么：

　　 已知圆周长度 $C$ 与半径 $r$ 的比值是一个固定值，由于以圆的半径作为弧长的度量单位，这就得到了算数式：

而一段圆弧 $l$ 如果是周长的 $\displaystyle\frac{n}{m}$，那么，它自然就可以表示为： 因此，弧长 $l$ 与半径 $r$ 之间建立了一一对应的关系。在圆的相关概念中提到，每段弧长都对应着一个圆心角。

　　 由于所有的圆都是相似的，对应同一圆心角的不同弧长之间的差异仅来源于圆的半径 $r$ 的不同。如果希望使新的圆心角度量方法不受半径 $r$ 的影响，需要消除半径 $r$ 的作用。将 $r$ 移到等式的左侧，可以得到：

这样，对于占圆周相同比例的圆弧，不论圆的半径 $r$ 多大，右侧的值始终保持不变。

2. 弧度制

　　 如果将式 4 右侧的值作为弧对应的圆心角的度量方式，那么通过定义 “以圆的半径作为弧长的度量单位”，人们得到了一个新的角度度量方法，这种方法满足之前提出的所有要求：

1. 它是一个无单位的纯数值。
2. 由于 “度” 在定义时采用了类似的按比例等分的原则，若规定整圆的圆心角为一个固定值，这种新的方式可以实现与传统的度分秒系统的快速转换。
3. 它仅依赖于常数 $\pi$。

　　 这种新的角度度量方法也就是弧度制（radian measure）。

　　 尽管之前说过 $\theta$ 是个数，但通常在物理上根据习惯，为了表示他是与角相关的量，会在后面加上单位 $ \,\mathrm{rad} $，读作弧度。注意，这只是为了在物理计算中与其他单位复合，表示它是角，本质上还是无量纲的。在数学研究中，一般也不会写 $ \,\mathrm{rad} $。

　　 根据圆的周长公式，圆周对应的圆心角为：

　　 也就是说，弧度中与 $360^\circ$ 对应的是 $2\pi$。根据上面的原理可以得到 $2\pi \,\mathrm{rad} $ 与 $360^\circ$ 对应，而根据定义 $0 \,\mathrm{rad} $ 与 $0^\circ$ 对应。若同一个角为 $a^\circ$ 与 $\theta \,\mathrm{rad} $ 通过对应关系化简可以得到二者的换算方法：

　　 由于弧度制消除了不同半径带来的影响，因此一般只研究单位圆（unit circle），即半径为 $1$ 的圆。可以认为，弧度就是圆心角在单位圆上所对的弧长。在单位圆中长度与半径相等的弧所对的圆心角就是 $1 \,\mathrm{rad} $。

　　 弧度制的引入使得圆的许多性质表达得更加简洁。例如，设半径为 $r$ 的圆弧对应的圆心角为 $\theta$（以弧度计），则有：

• 由弧度的定义可得弧长 $l = r\theta$；
• 扇形面积为 $\displaystyle S = \frac{1}{2} r^2 \theta$，或用弧长表示为 $\displaystyle S = \frac{1}{2} l r$。

　　 值得注意的是，扇形面积公式 $\displaystyle S = \frac{1}{2} l r$ 与三角形面积公式 $\displaystyle S = \frac{1}{2} bh$ 形式相同。这可以通过几何解释来直观理解。设想一个角度 $\theta$ 极小的扇形，其形状近似于一个三角形，其中弧长 $l$ 近似为底边，高为半径² $r$。更一般地，可以将扇形视为由无数个极窄的三角形组成，每个三角形的高均为 $r$，而底边依弧线分布。由于这一极限过程，扇形面积公式自然呈现出三角形面积的形式。需要注意的是，此处的分析是定性的，旨在帮助理解公式的直观来源。

3. 任意角

　　 在之前的学习中，角被定义为由一个公共端点引出的两条射线之间的夹角，并根据大小分类为锐角、直角、钝角、平角和周角。然而，当角度超过 $180^\circ$ 时，人们常采用等价的较小角度来表示，例如用 $360^\circ$ 减去该角度。例如，一个 $210^\circ$ 的角常被描述为 $360^\circ - 210^\circ = 150^\circ$，这样可以将角限制在 $180^\circ$ 以内，使其仍然符合常见的锐角、直角和钝角的分类。这种方法在仅关注角度大小时十分直观。

　　 然而，在跳水运动员的空中翻转、机械部件的旋转等实际场景中，角度不仅用于测量静态夹角，还需要描述动态的旋转过程。这时，人们通过抽象这个过程，通过旋转的视角来理解角：设定一条始边（initial side），然后围绕其端点旋转，最终到达终边（terminal side）。旋转的角度即为从初始边到终边的变化量。这种定义方式不仅兼容原有的角度概念，还能直接地描述旋转现象。

　　 这种角的定义解决了旋转的问题，但如果仍然使用 $0^\circ$ 到 $360^\circ$ 之间的角度来表示旋转，可能会导致信息丢失，主要体现在以下两种情况：

1. 当旋转角度超过 $180^\circ$ 时，尽管逆时针旋转 $210^\circ$ 和顺时针旋转 $150^\circ$ 后终边位置相同，但旋转路径不同。逆时针旋转 $210^\circ$ 经过了更大的角度，而顺时针旋转 $150^\circ$ 则是较短路径。因此，仅用终边位置描述角度，无法准确体现旋转的过程。
2. 设想一个车轮上的某个辐条在不断旋转。虽然辐条会多次回到相同的位置，但它实际经历了不同的旋转圈数，或者循环。如果仅用 $0^\circ$ 到 $360^\circ$ 之间的角度来表示，就无法区分它转动的圈数或循环的次数。

　　 由此可见，在修改角的定义后，需要扩展角的表示方法，使其不仅能表示一个固定的几何量，还能描述物体的连续运动。这类似于数系的拓展，例如，引入实数后，数学系统可以表示 $\sqrt{2}$ 这样的无理数，而不仅仅局限于有理数。下面分别针对每个问题讨论：

1. 区分旋转方向。这比较容易想，与整数区分正负的方式类似，把逆时针、顺时针对应成正数、负数，静止不动对应成 $0$。至于该把逆时针对应为正，还是顺时针对应为正呢？通常，约定选择逆时针为正方向。这主要是由于笛卡尔坐标系的建立方式。在平面直角坐标系中，$x$ 轴向右，$y$ 轴向上，从 $x$ 轴正方向旋转到 $y$ 轴正方向的方向是逆时针，因此自然将其定义为正方向。这一约定更深层的原因是可以使得线性代数、向量运算、叉积、电磁学、计算机图形学等领域保持统一，也更符合许多自然现象的规律。
2. 区分旋转圈数。两种方案可以实现这个目的：一是引入新的单位 “圈”，规定 $1\text{圈}=360^\circ$；二是直接取消 “角度必须在周角以内” 的限制，让角度自由扩展。前者虽然符合日常语言习惯，比如 “转了一圈”，但在数学上并不自然，就像角度制计算中额外转化分、秒一样，圈的引入会让计算变得更加离散，不利于运算的简化。此外，实际应用中角度往往是连续变化的，而 “圈” 作为单位太大，无法精确描述微小增量，因此并无额外优势。从数学的发展来看，更合理的做法是让角度可以无限扩展，以保持运算的封闭性和可计算性，使计算更加直接，无需额外拆分和归约，而不是人为增加一个新单位。

　　 综上，数学引入了 “任意角” 的概念。

　　 这一扩展不仅让角度的表示方式更加统一，还让数学计算更自然，为后续的三角函数、旋转变换等概念奠定了基础。

　　 早期的三角学发展是基于单位圆和弧长的概念，单位圆的思路使得角度可以与弧长直接对应，而解除角度的限制，使其能够自由扩展，与实数向两侧延伸的方式保持一致。这种视角下，角度不仅仅是几何图形中的静态量，而是可以连续变化的数值，因此弧度制成为了数学上描述任意角的自然选择。弧度制的本质是用单位圆上对应弧的长度来测量角度，使得角度的定义与数轴上的实数直接关联，而不依赖于人为设定的度数系统。

　　 综上，角的概念推广后，在弧度制下，角的集合与实数集 $\mathbb{R}$ 之间建立了一一对应关系。弧度制与任意角的结合，使得角的大小可以用十进制实数自然表示，使得实数不仅与线段上的点一一对应，同时也与角度大小一一对应，从而构建起更具一般性的数学框架。

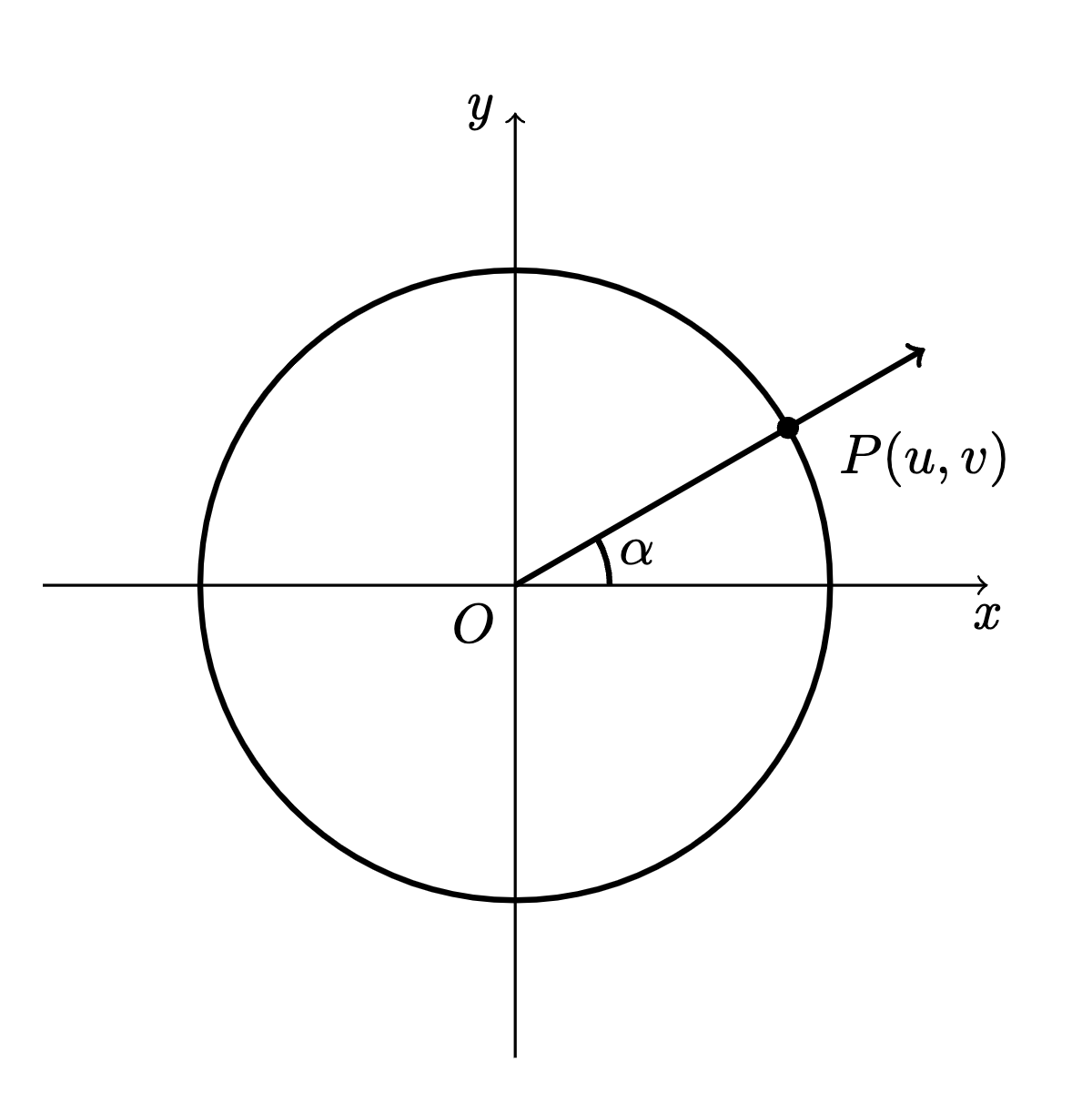
　　 为方便研究，通常将角的顶点放在坐标系原点，始边放在 $x$ 轴正方向上。这时，角的终边（除端点外）所在的象限决定了该角的象限归属。例如，若终边落在第一象限，则称该角为第一象限角，其他象限类推。

　　 另外，所有与某个角 $\alpha$ 终边相同的角，可构成一个集合：

　　 这表示任何角 $\alpha$ 只要增加或减少整数倍的 $2\pi$（即完整旋转若干圈），其终边位置保持不变。这个集合反映了角的周期性，在三角函数、旋转变换等问题中具有重要作用。

---

1. ^ 马瑞芳, 库在强. 数学史融入弧度制的教学设计研究[J]. 教育进展, 2023, 13(8): 5911-5919.
2. ^ 因为半径与弧的切线垂直，而角度很小时，弧近似于切线。