傅里叶变换的数值计算、快速傅里叶变换(Matlab)
贡献者: addis
1. 直接数值积分
作为下文 FFT 方法的参照,我们先实现直接用数值积分计算傅里叶变换(式 1 )。调用时需要提供一元函数(句柄)f,而不是一系列离散函数值。xspan 是对 f 积分的区间,而 kspan 是输出中 k 的区间,Nk 是 k 的长度。这么做虽然直观且精确,但计算量较大,所以一般还是用下一节中的 FFT 方法。
尤其是如果 f 并不是通过函数给出,而只是一系列等间距的散点,那么与其先插值再做数值积分,FFT 方法是最适合的,因为 FFT 已经相当于对散点进行了 sinc 插值(子节 4 )。
代码 1:CFT.m
% Continuous Fourier Transform by Integration
% f must be a function handle
% gh is function handle, g = gh(linspace(kmin,kmax,Nk))
% input the 7th argument to plot spectrum
function [k,g,gh] = CFT(f,xspan,kspan,Nk,~)
k = linspace(kspan(1),kspan(2),Nk);
g = zeros(1,Nk);
for ii = 1:Nk
integrand = @(x) f(x).*exp(-1i*k(ii)*x);
g(ii) = integral(integrand,xspan(1),xspan(2), 'AbsTol',1e-8);
end
g = g/sqrt(2*pi);
if nargin == 5
figure; plot(k,g);
end
if nargout == 3
gh = @(kq) interp1(k,g,kq,'spline');
end
end
代码 2:iCFT.m
% Continuous Fourier Transform by Integration
% g must be a function handle
% fh is function handle, f = fh(linspace(xmin,xmax,Nx))
% input the 7th argument to plot spectrum
function [x,f,fh] = iCFT(g,kspan,xspan,Nx,~)
x = linspace(xspan(1),xspan(2),Nx);
f = zeros(1,Nx);
for ii = 1:Nx
integrand = @(k) g(k).*exp(1i*k*x(ii));
f(ii) = integral(integrand,kspan(1),kspan(2), 'AbsTol',1e-8);
end
f = f/sqrt(2*pi);
if nargin == 5
figure; plot(x,f);
end
if nargout == 3
fh = @(xq) interp1(x,f,xq,'spline');
end
end
2. 用 FFT 近似傅里叶变换
这里使用的算法见子节 7 。给出任意等间距的 $x$ 坐标格点 [x0, x0+dx, x0+2*dx, ...],以及对应的函数值 f = [f(1), f(2), ...],那么该代码可以通过 Matlab 提供的快速傅里叶变换(FFT)计算傅里叶变换(式 1 )。输入中 Nk 是可选的,默认等于 x 的个数。若 Nk 大于 f 的个数,输出中 k 的步长将会相应变小使 k 的长度为 Nk,但区间不会变。k 的区间是由 dx 决定的。在实现上,当 Nk > numel(f) 时会预先在 f 两边添加 0 使其先具有 Nk 个元。
代码 3:FFT.m
% fft approximation of the analytical fourier transform from f(x) to g(k)
% x and k are both equally spaced, x starts from x0 equally spaced by dx
% norm(g) = norm(f)
% numel(g) = Nk
function [g, k] = FFT(f, x0, dx, Nk, k_mid)
N = numel(f);
if ~isvector(f)
error('f must be a vector!');
end
if ~exist('k_mid', 'var')
k_mid = 0;
end
if ~exist('Nk', 'var')
Nk = N;
end
f = reshape(f, 1, N);
x_mid = x0 + ceil((N-1)/2)*dx;
if k_mid ~= 0
x = linspace(x0, x0+dx*(N-1), N);
f = f .* exp(-1i*k_mid*(x-x_mid));
end
if Nk > N
N = Nk;
f = fftresize(f, N);
end
g = sffts(f)*(dx/sqrt(2*pi));
k = fftlinspace(2*pi/dx, N) + k_mid;
if (abs(x_mid/x0) > 2*eps)
g = g .* exp(-1i*k*x_mid);
end
end
代码 4:iFFT.m
% ifft approximation of the analytical inverse Fourier transform
% from g(k) to f(x)
% x and k are both equally spaced, k starts from k0 equally spaced by dk
% norm(g) = norm(f)
% numel(f) = Nx
function [f, x] = iFFT(g, k0, dk, Nx, x_mid)
N = numel(g);
if ~isvector(g)
error('g must be a vector!');
end
if ~exist('x_mid', 'var')
x_mid = 0;
end
if ~exist('Nx', 'var')
Nx = N;
end
g = reshape(g, 1, N);
k_mid = k0 + ceil((N-1)/2)*dk;
if x_mid ~= 0
k = linspace(k0, k0+dk*(N-1), N);
g = g .* exp(1i*x_mid*k);
end
if Nx > N
N = Nx;
g = fftresize(g, N);
end
f = siffts(g)*(N*dk/sqrt(2*pi));
x = fftlinspace(2*pi/dk, N) + x_mid;
if (abs(k_mid/k0) > 2*eps)
f = f .* exp(1i*k_mid*(x-x_mid));
end
end
下面是一些依赖程序
代码 5:fftresize.m
% resize vector/matrix length for ftt by zero padding on both ends
function y = fftresize(x, newN)
% === x is row vector ===
if size(x, 1) == 1
N = numel(x);
Ndiff = abs(newN - N);
if newN > N % 0-padding
if mod(Ndiff,2) == 0
Ndiff = 0.5*Ndiff;
y = [zeros(1, Ndiff), x, zeros(1, Ndiff)];
else
Ndiff = 0.5*(Ndiff-1);
if mod(N, 2) == 0
y = [zeros(1, Ndiff), x, zeros(1, Ndiff+1)];
else
y = [zeros(1, Ndiff+1), x, zeros(1, Ndiff)];
end
end
elseif newN < N % shrink
y = shrink(x, N, Ndiff);
else
y = x;
end
% === x is column vector ===
elseif size(x, 2) == 1
N = numel(x);
Ndiff = abs(newN - N);
if newN > N % 0-padding
if mod(Ndiff,2) == 0
Ndiff = 0.5*Ndiff;
y = [zeros(Ndiff, 1); x; zeros(Ndiff, 1)];
else
Ndiff = 0.5*(Ndiff-1);
if mod(N, 2) == 0
y = [zeros(Ndiff, 1); x; zeros(Ndiff+1, 1)];
else
y = [zeros(Ndiff+1, 1); x; zeros(Ndiff, 1)];
end
end
elseif newN < N % shrink
y = shrink(x, N, Ndiff);
else
y = x;
end
% === x is matrix ===
else
[N, Ncol] = size(x);
Ndiff = abs(newN - N);
if newN > N % 0-padding
if mod(Ndiff,2) == 0
Ndiff = 0.5*Ndiff;
y = [zeros(Ndiff, Ncol); x; zeros(Ndiff, Ncol)];
else
Ndiff = 0.5*(Ndiff-1);
if mod(N, 2) == 0
y = [zeros(Ndiff, Ncol); x; zeros(Ndiff+1, Ncol)];
else
y = [zeros(Ndiff+1, Ncol); x; zeros(Ndiff, Ncol)];
end
end
elseif newN < N % shrink
if mod(Ndiff,2) == 0
Ndiff = 0.5*Ndiff;
y = x(Ndiff+1:end-Ndiff, :);
else
Ndiff = 0.5*(Ndiff-1);
if mod(N, 2) == 0
y = x(Ndiff+2:end-Ndiff, :);
else
y = x(Ndiff+1:end-Ndiff-1, :);
end
end
else
y = x;
end
end
end
function y = shrink(x, N, Ndiff)
if mod(Ndiff,2) == 0
Ndiff = 0.5*Ndiff;
y = x(Ndiff+1:end-Ndiff);
else
Ndiff = 0.5*(Ndiff-1);
if mod(N, 2) == 0
y = x(Ndiff+2:end-Ndiff);
else
y = x(Ndiff+1:end-Ndiff-1);
end
end
end
代码 6:sffts.m
% shifted fft
function y = sffts(x, dim)
if nargin < 2
y = fftshift(fft(ifftshift(x)));
else
y = fftshift(fft(ifftshift(x, dim),[], dim), dim);
end
end
代码 7:fftlinspace.m
% generate N grid points from bandwidth
% input 2 or 3 arguments
function x = fftlinspace(L, N, x0)
if mod(N, 2) == 0
Lh = 0.5*L; dx = L/N;
if nargin == 3
x = linspace(-Lh+x0, Lh-dx+x0, N);
else
x = linspace(-Lh, Lh-dx, N);
end
else
a = (N-1)*L/(2*N);
if nargin == 3
x = linspace(-a+x0, a+x0, N);
else
x = linspace(-a, a, N);
end
end
end
示例
% === params ===
x0 = -6; dx = 0.05; N = 300;
Nk = 4*N; k_mid = 0.25;
a = 2; x_shift = 0.8; k_shift = 2;
f_anal = @(x) exp(-a*(x-x_shift).^2) .* exp(1i*k_shift*(x-x_shift));
g_anal = @(k) exp(-(k-k_shift).^2/(4*a))/sqrt(2*a) .* exp(-1i*x_shift*k);
% =============
close all;
x = linspace(x0, x0+dx*(N-1), N).';
x_mid = x0 + ceil((N-1)/2)*dx;
[g, k] = FFT(f_anal(x), x0, dx, Nk, k_mid);
k = k(:); g = g(:);
k0 = k(1); dk = k(2)-k(1);
[f_, x_] = iFFT(g, k0, dk, N, x_mid);
f_ = f_(:); x_ = x_(:);
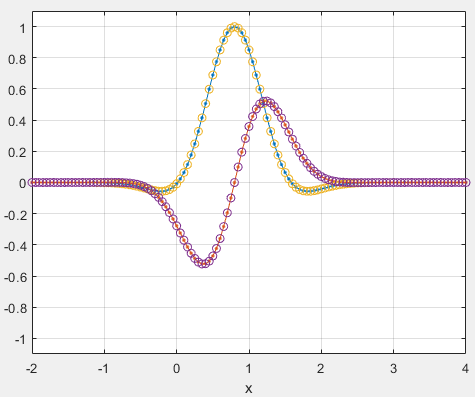
figure; plot(x, [real(f_anal(x)), imag(f_anal(x))], '.-');
hold on; plot(x_, [real(f_) imag(f_)], 'o');
grid on; axis([-2, 4, -1.1, 1.1]);
xlabel x;
figure; plot(k, [real(g_anal(k)), imag(g_anal(k))], '.-');
hold on; plot(k, [real(g), imag(g)], 'o');
grid on; axis([-7, 10, -0.6, 0.6]);
xlabel k;
图 1:输出 $f(x)$
图 2:输出 $g(k)$
傅里叶级数
根据式 12 ,傅里叶级数与傅里叶变换值相差一个常数:
代码 8:FS.m
% Fourier series by FFT
function [C, k] = FS(f, x0, dx)
[g, k] = FFT(f, x0, dx, Nk, dim);
C = sqrt(2*pi)/(N*dx) * g;
end
3. sinc 插值
根据采样定理,可以使用 FFT 对函数的离散值进行 sinc 插值,dx 是可选的。
代码 9:fftinterp.m
% approximate sinc interpolation by fft
% N is optional, used to zero-pad f
function [f1, x1] = fftinterp(f, N1, dx, N)
if ~exist('N','var') || isempty(N)
N = numel(f);
else
f = fftresize(f, N);
end
f1 = siffts(fftresize(sffts(f), N1))*N1/N;
if nargout == 2
x1 = fftlinspace(dx*N, N1);
end
end
为了对比验证,我们也可以直接实现 sinc 插值,但该代码的效率较低
代码 10:sinc_interp.m
% sinc_interp
function y = sinc_interp(x, x0, y0)
N0 = numel(x0);
y = zeros(size(x));
dx0 = (max(x0)-min(x0))/(numel(x0)-1);
a = pi/dx0;
for ii = 1:N0
y = y + y0(ii).*sinc(a*(x-x0(ii)));
end
end
function y = sinc(x)
mask = (x~=0);
y(mask) = sin(x(mask))./x(mask);
y(~mask) = 1;
end
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。
友情链接: 超理论坛 | ©小时科技 保留一切权利