贡献者: 零穹; addis
本节介绍利用已知函数点近似函数导数的方法,以及相应的计算机处理,它们将给出所谓的差分矩阵。这一内容将使我们能够更快过渡到谱方法。
我们从这样的问题开始:给定一组点 $\{x_i\}$ 和对应的函数值 $u(x_i)$,我们如何使用这些数据近似 $u$ 的导数呢?
1. 差分近似
最直接的想法就是进行有限差分。考虑点 $\{x_i\}$ 是均匀分布的,并记 $x_{i+1}-x_i=h$,则该式对每一 $i$ 都成立。
记 $w_i$ 为 $u'(x_i)$ 的近似值。那么标准的二阶有限差分近似为
\begin{equation}
w_i=\frac{u_{i+1}-u_{i-1}}{2h}.~
\end{equation}
所谓的几阶近似公式是指
定义 1 $n$ 阶近似
称函数 $u(x)$ 是 $f(x)$(关于 $h$)的$n$ 阶近似,是指对任一点 $x_i$,$ \left\lvert f(x_i)-u(x_i) \right\rvert $ 是关于 $h^n$ 的高阶无穷小,即 $\lim_{h\rightarrow0}\frac{ \left\lvert f(x_i)-u(x_i) \right\rvert }{h^n}=0$1。
让我们证明式 1 的差分公式确实是 $u$ 关于 $h$ 的二阶近似。
证明:利用该泰勒展开
\begin{equation}
\begin{aligned}
f(x_i+h)&=f(x_i)+f'(x_i)h+\frac{1}{2}f''(x_i)h^2+\frac{1}{6}f'''(x_i)h^3+o(h^3),\\
f(x_i-h)&=f(x_i)-f'(x_i)h+\frac{1}{2}f''(x_i)h^2-\frac{1}{6}f'''(x_i)h^3+o(h^3).
\end{aligned}~
\end{equation}
因此
\begin{equation}
f(x_i+h)-f(x_i-h)=2hf'(x_i)+\frac{1}{3}h^3f'''(x_i)+o(h^3).~
\end{equation}
即
\begin{equation}
\begin{aligned}
f'(x_i)&=\frac{f(x_i+h)-f(x_i-h)}{2h}-\frac{1}{3}h^3f'''(x_i)-o(h^3)\\
&=\frac{f(x_i+h)-f(x_i-h)}{2h}+o'(h^2).
\end{aligned}~
\end{equation}
因此,
式 1 表明
\begin{equation}
\left\lvert u'_i-w_i \right\rvert = \left\lvert u'_i-\frac{u_{i+1}-u_{i-1}}{2h} \right\rvert = \left\lvert o(h^2) \right\rvert .~
\end{equation}
证毕!
2. 差分矩阵
式 1 告诉我们,已知点 $\{x_i\}$ 处的函数值 $\{u_i\}$,我们可以得到函数 $u$ 在这些点的导数近似 $\{w_i\}$。但是,这一公式仅仅给我们非端点 $i=0,i=N$($N$ 为 $i$ 的最大取值)处的导数近似。也就是说,若我们通过已知点逐次近似函数的高阶导数,则能通过式 1 近似函数高阶导数的点数会依次减少端点处的 2 个。
然而,若认为 $u$ 关于 $x$ 是周期性的,即 $u_0=u_N,u_i=u_{N+i}$,那么端点处的导数近似公式就为
\begin{equation}
w_0=\frac{u_{1}-u_{-1}}{2h}=\frac{u_{1}-u_{N-1}}{2h}=w_N.~
\end{equation}
这样就不会使得能近似高阶导数的点数减少
2。在函数的周期性假设下,结合
式 1 和
式 6 就有
\begin{equation}
\begin{pmatrix}
w_1\\
\\
\\
\vdots\\
\\
w_N
\end{pmatrix}=h^{-1}\begin{pmatrix}
0&1/2&&&&-1/2\\
-1/2&0&&\ddots&&\\
&&&\ddots&&\\
&&&\ddots&0&1/2\\
1/2&&&&-1/2&0\\
\end{pmatrix}\begin{pmatrix}
u_1\\
\\
\\
\vdots\\
\\
u_N
\end{pmatrix}.~
\end{equation}
注意
式 1 表明 $u_i$ 的系数矩阵在第 $i$ 行的非零元只有 $i+1$ 和 $i-1$ 处的。即对角元的两边,并且符号相反。因此非零元刚好在对角线两边的 “对角线”,左下角和右上角的数值来源于
式 6 。明显的,该矩阵是一个
Toeplitz 矩阵。由于它来源于差分公式,因此也被称为
差分矩阵。
3. 从多项式插值角度看差分公式
差分公式式 1 还可以从二阶多项式插值法3获得。这一角度使我们能够推广到一般的高阶多项式内插公式。
该思路是这样的:设函数 $u$ 是 $n$ 次多项式,则每一点的导数自然可以通过多项式求导得到。通过多项式插值法可以得到过已知数据点的多项式,接着多项式的导数在已知点的取值就得到数据点处的函数导数的多项式近似值。
对于二阶多项式近似,函数在点 $\{x_i\}$ 取值 $\{u_i\}$ 的二次多项式(多项式近似通过的 3 个点取 $x_{i-1},x_i,x_{i+1}$)为
\begin{equation}
\begin{aligned}
p_i(x)=&u_{i-1}(x-x_i)(x-x_{i+1})/2h^2\\
&-u_{i}(x-x_{i-1})(x-x_{i+1})/h^2\\
&+u_{i+1}(x-x_i)(x-x_{i-1})/2h^2\\
=& u_{i-1}a_{-1}(x)+u_{i}a_0(x)+u_{i+1}a_1(x).
\end{aligned}~
\end{equation}
其中
\begin{equation}
\begin{aligned}
& a_{-1}(x):=(x-x_i)(x-x_{i+1})/2h^2,\\
&a_{0}(x):=-(x-x_{i-1})(x-x_{i+1})/h^2,\\
&a_{1}(x):=(x-x_i)(x-x_{i-1})/2h^2.
\end{aligned}~
\end{equation}
带入 $x_{i-1},x_i,x_{i+1}$ 可知,$p_i(x_{i-1})=u_{i-1},p_i{x_{i}}=u_i,p(x_{i+1})=u_{i+1}$。通过求导数 $p_i'(x)$ 并令 $x=x_i$ 取值,可得
式 1 。
$2n$ 阶多项式插值的差分公式
为方便起见,以偶数阶为例,即可设为 $2n$ 阶多项式插值,其过 $2n+1$ 个点 $u_{i+j},j=-n,-n+1,\cdots ,n$ 只需注意 $p_i(x_{i-j})=u_{i-j},u_{i}=u_{}$,注意式 8 的规律,因此 $2n$ 阶多项式插值公式为(设 $x_{i+2n}=x_i$)
\begin{equation}
p_i(x)=\sum_{j=-n}^n u_{i+j}a_{j}(x),~
\end{equation}
其中
\begin{equation}
\begin{aligned}
a_{j}(x)=&(-1)^{n-j}(x-x_{i-n})(x-x_{i-n+1})\cdots(x-x_{i+j-1})\\
&\cdot(x-x_{i+j+1})\cdots(x-x_{i+n})/((j+n)!(n-j)!h^{2n}).
\end{aligned}~
\end{equation}
只要求出 $p'(x_i)$ 即可得到对应的 $n$ 阶差分方程。(建议读者只需明白具体的思路,无需大量的进行计算,因为计算量会随着 $n$ 的增大而增大,实际上以下的具体实例都是由 Mathematica 辅助计算完成)例如,对 4 阶($n=2$),就有
\begin{equation}
w_i=\frac{u_{i-2}}{12 h}+\frac{2 u_{i+1}}{3 h}-\frac{2 u_{i-1}}{3 h}-\frac{u_{i+2}}{12 h}.~
\end{equation}
对 6 阶($n=3$),就有
\begin{equation}
\begin{aligned}
w_i=&-\frac{u_{i-3}}{60 h}+\frac{3 u_{i-2}}{20 h}+\frac{3 u_{i+1}}{4 h}\\
&+\frac{u_{i+3}}{60 h}-\frac{3 u_{i-1}}{4 h}-\frac{3 u_{i+2}}{20 h}.
\end{aligned}~
\end{equation}
因此,若设有 $8$ 个数据点,即 $x_i$ 的个数为 $8$。那么,对应 $4$ 阶和 6 阶多项式插值的差分矩阵分别就是
\begin{equation}
\left(
\begin{array}{cccccccc}
0 & \frac{2}{3 h} & -\frac{1}{12 h} & 0 & 0 & 0 & \frac{1}{12 h} & -\frac{2}{3 h} \\
-\frac{2}{3 h} & 0 & \frac{2}{3 h} & -\frac{1}{12 h} & 0 & 0 & 0 & \frac{1}{12 h} \\
\frac{1}{12 h} & -\frac{2}{3 h} & 0 & \frac{2}{3 h} & -\frac{1}{12 h} & 0 & 0 & 0 \\
0 & \frac{1}{12 h} & -\frac{2}{3 h} & 0 & \frac{2}{3 h} & -\frac{1}{12 h} & 0 & 0 \\
0 & 0 & \frac{1}{12 h} & -\frac{2}{3 h} & 0 & \frac{2}{3 h} & -\frac{1}{12 h} & 0 \\
0 & 0 & 0 & \frac{1}{12 h} & -\frac{2}{3 h} & 0 & \frac{2}{3 h} & -\frac{1}{12 h} \\
-\frac{1}{12 h} & 0 & 0 & 0 & \frac{1}{12 h} & -\frac{2}{3 h} & 0 & \frac{2}{3 h} \\
\frac{2}{3 h} & -\frac{1}{12 h} & 0 & 0 & 0 & \frac{1}{12 h} & -\frac{2}{3 h} & 0 \\
\end{array},
\right)~
\end{equation}
和
\begin{equation}
\begin{aligned}
\left(
\begin{array}{cccccccc}
0 & \frac{3}{4 h} & -\frac{3}{20 h} & \frac{1}{60 h} & 0 & -\frac{1}{60 h} & \frac{3}{20 h} & -\frac{3}{4 h} \\
-\frac{3}{4 h} & 0 & \frac{3}{4 h} & -\frac{3}{20 h} & \frac{1}{60 h} & 0 & -\frac{1}{60 h} & \frac{3}{20 h} \\
\frac{3}{20 h} & -\frac{3}{4 h} & 0 & \frac{3}{4 h} & -\frac{3}{20 h} & \frac{1}{60 h} & 0 & -\frac{1}{60 h} \\
-\frac{1}{60 h} & \frac{3}{20 h} & -\frac{3}{4 h} & 0 & \frac{3}{4 h} & -\frac{3}{20 h} & \frac{1}{60 h} & 0 \\
0 & -\frac{1}{60 h} & \frac{3}{20 h} & -\frac{3}{4 h} & 0 & \frac{3}{4 h} & -\frac{3}{20 h} & \frac{1}{60 h} \\
\frac{1}{60 h} & 0 & -\frac{1}{60 h} & \frac{3}{20 h} & -\frac{3}{4 h} & 0 & \frac{3}{4 h} & -\frac{3}{20 h} \\
-\frac{3}{20 h} & \frac{1}{60 h} & 0 & -\frac{1}{60 h} & \frac{3}{20 h} & -\frac{3}{4 h} & 0 & \frac{3}{4 h} \\
\frac{3}{4 h} & -\frac{3}{20 h} & \frac{1}{60 h} & 0 & -\frac{1}{60 h} & \frac{3}{20 h} & -\frac{3}{4 h} & 0 \\
\end{array}
\right)
\end{aligned}~
\end{equation}
4. Mathematica 实操
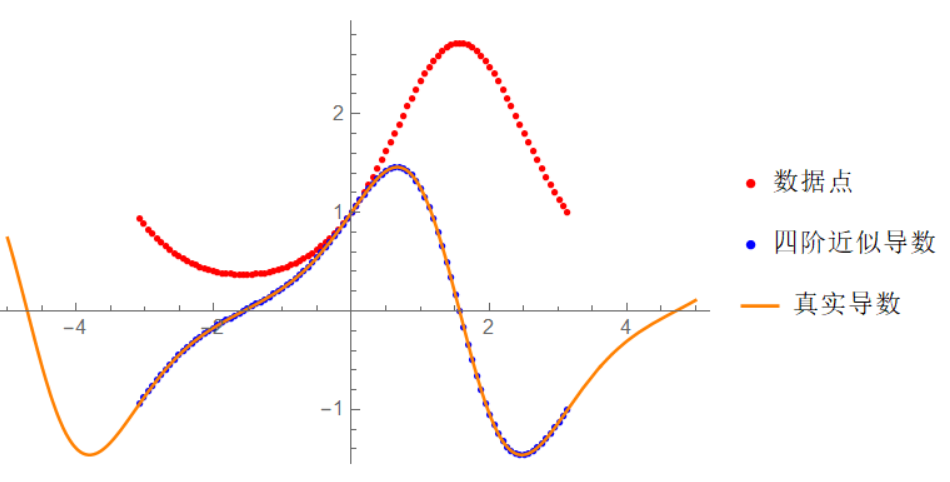
以下通过 $u(x)=e^{\sin x}$ 产生 100 个数据点,并用 4 阶差分矩阵求数据点的导数,并和实际导数进行比较。
代码 1:Mathematica 利用四阶差分矩阵求导数,数据点由 $u(x)=e^{\sin x}$ 产生
(*For[i=1,i\[LessEqual]10,
AppendTo[nn,n];*)
n = 100;(*数据点个数*)
A1[n_] :=
SparseArray[{1 -> 0, 2 -> -2/3, 3 -> 1/12, n - 1 -> -1/12,
n -> 2/3}, n];(*第一列*)
A2[n_] :=
SparseArray[{1 -> 0, 2 -> 2/3, 3 -> -1/12, n - 1 -> 1/12,
n -> -2/3}, n];(*第一行*)
T4[n_] := ToeplitzMatrix[A1[n], A2[n]];(*四阶差分矩阵*)
h = 2 Pi/n; xi = Table[N[-Pi + i h], {i, 1, n}]; u =
Exp[Sin[xi]];(*通过函数u=Exp[Sin[xi]]产生n个数据点u_i*)
w = T4[n].u/h;(*n个点的导数近似*)
Plot1 = ListPlot[Transpose[{xi, u}], PlotStyle -> Red,
PlotLegends -> {"数据点"}];(*数据点的图像*)
Plot2 = ListPlot[Transpose[{xi, w}], PlotStyle -> Blue,
PlotLegends -> {"四阶近似导数"}];(*四阶差分算法求得的导数*)
Plot3 = Plot[Cos[x] Exp[Sin[x]], {x, -5, 5}, PlotStyle -> Orange,
PlotLegends -> {"真实导数"}];(*实际导数*)
Show[Plot1, Plot2, Plot3, PlotRange -> All]
所得结果如下图
图 1:4 阶差分矩阵求导结果
从图中可看出,模拟结果很好的符合真实值(差分矩阵得到的结果很好的落在了真实导数曲线上)。
1. ^ 在数学分析里,这被记作 $ \left\lvert f(x_i)-u(x_i) \right\rvert =o(h^n)$
2. ^ 这并不是说这样的处理更合理,而只能让我们能求得 $u$ 满周期性条件时每个点的高阶导数。倘若 $u$ 是非周期的,那么所得的各阶近似就不可信,但是对于没有在求高阶导过程中消掉的 “中间点” 的值却仍然是合理的。
3. ^ $n$ 阶插值法可理解为通过 $n+1$ 个已知点的 $n$ 次多项式近似
致读者: 小时百科一直以来坚持所有内容免费无广告,这导致我们处于严重的亏损状态。 长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。 因此,我们请求广大读者
热心打赏 ,使网站得以健康发展。 如果看到这条信息的每位读者能慷慨打赏 20 元,我们一周就能脱离亏损, 并在接下来的一年里向所有读者继续免费提供优质内容。 但遗憾的是只有不到 1% 的读者愿意捐款, 他们的付出帮助了 99% 的读者免费获取知识, 我们在此表示感谢。