深度优先搜索（DFS）

贡献者： 有机物

　　 深度优先搜索（DFS，Depth First Search）简称深搜或者爆搜，DFS 的搜索顺序是按照深度优先搜索，简单来说就是 “一条路走到黑”，搜索是把所有方案都试一遍，再判断是不是一个可行解。搜索与 “递归” 和 “栈” 有很大的联系，递归是实现搜索的一种方式，而栈则是计算机实现递归的方式。每个搜索过程都对应着一棵递归搜索树，递归搜索树可以让我们更加容易的理解 DFS。 整个搜索过程就是基于该搜索树完成的，为了不重复遍历每个结点，会对每个结点进行标记，也可以对树中不可能是答案的分支进行删除，从而更高效的找到答案，这种方法被称为剪枝。如果搜索树在某个子树中搜索到了叶结点，想继续搜索只能返回上个或多个状态，返回的过程称为回溯，回溯要记得恢复状态，才能保证接下来的搜索过程可以正常进行。

1. 普通搜索

　　 来看一道具体例题学习 DFS

　　 题意：输出 $n$ 的全排列

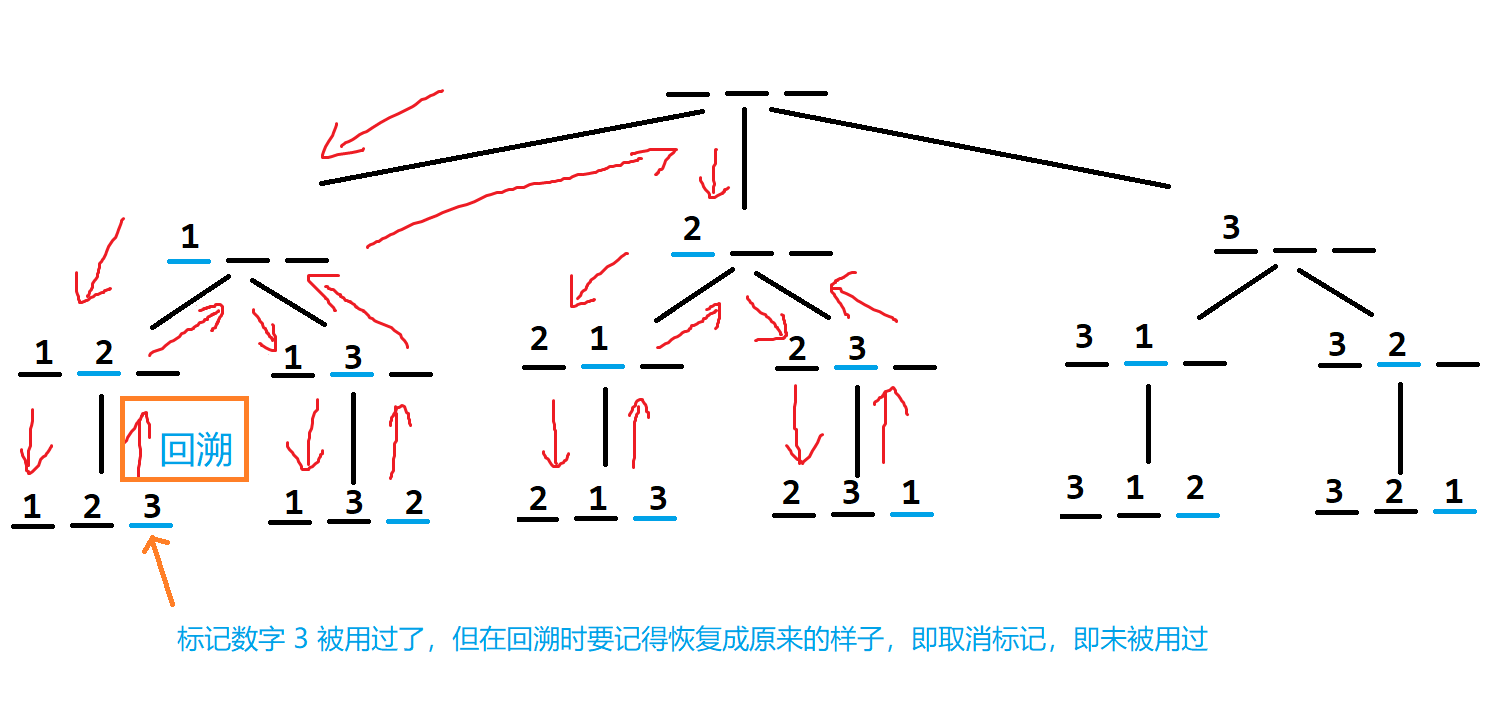
　　 思路：以 $n$ 为 $3$ 举例，枚举每个位置上该填什么数，但是每一位上的数不能和其他位置上的数一样，填满了 $3$ 位就输出，然后回溯继续搜索。

　　 上图则是一棵递归搜索树，就是搜索的过程形象化的显示出来。从第一个数字开始填，在填第二个数字，填过的数字记得要标记一下 “使用过了”，不然会导致三个数字有两个数字是重复的。上文提到的回溯，就是填完了三个数字，先输出答案，无法在继续搜索下去就要回溯，回溯记得要恢复状态，不然接下来无法填数。

　　 算法思路：

1. 用 path 数组保存排列。
2. 用 st 数组保存每个数的状态，st[i] 为 $\mathtt{true}$ 则表示数字 $i$ 被用过，反之没被用过。

int path[10], st[10], n;

void dfs(int u)
{
    if (u == n) // u == n 则说明填满了三个数
    {
        for (int i = 0; i < n; i ++ )
            cout << "    " << path[i];     // 输出答案
        cout << endl;
        return;     // 返回，进行回溯操作
    }
    
    for (int i = 1; i <= n; i ++ )
        if (!st[i])
        {
            st[i] = true;   // 标记数字 i 被使用过
            path[u] = i;    // 第 u 个位置上的数是 i
            
            dfs(u + 1);     // 搜下一个位置
            
// 如果开始执行这段代码了，说明已经填满了 3 个数，正在进行回溯操作，则需要恢复状态
            st[i] = false;  
// 第 u 个位置变成空了，但这句话其实没必要写，在回溯完毕准备填数的时候则会被覆盖
            path[u] = 0;    
        }
        
    return;     // 回溯
}

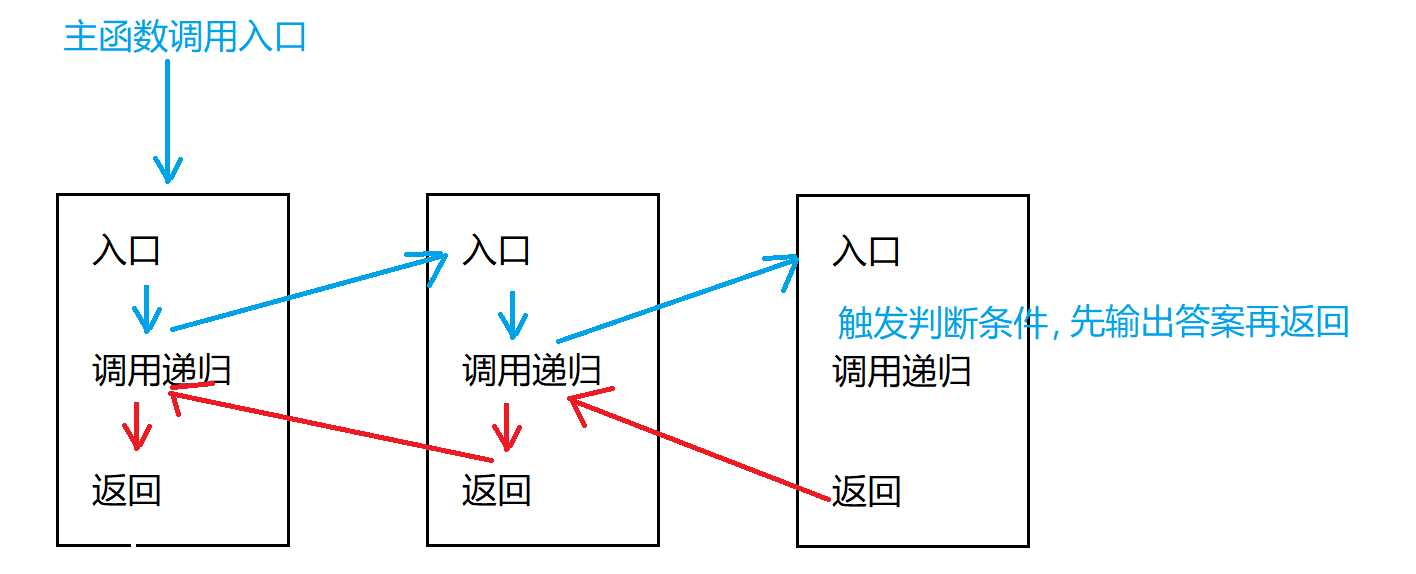
　　 DFS 的思想和代码很容易理解，这里不再赘述，但初学者学不懂 DFS 的原因主要是不理解递归而理解不了 DFS。这里来详细的讲解一下递归的执行过程。

　　 进入入口则是主函数调用，先执行一段代码然后递归调用（对应上面的代码就是 dfs(u+1)），如果某一次递归的过程的中触发了判断条件，则返回（回溯），回溯到上次执行我这次的递归的代码的下面再继续执行下面的代码，如图中的第一根红线，对应上面的代码是先输出了 $1 2 3$，然后是第一次触发判断条件，这时 $u$ 为 $3$，就返回到 $u$ 为 $2$ 的这次递归上，然后不执行 dfs(u+1)，直接执行下面的代码。然后没代码可以执行了，就只能执行第 $27$ 行的代码继续返回（回溯），然后再继续做接下来的操作。

2. 搜索的剪枝

　　 搜索的剪枝是优化搜索的很好的一种方式，即及时排除不可能的答案，从而少搜索点结点，就可以优化时间。在递归搜索树中则是删除一个子树，则被成为 “剪枝”。

　　 剪枝的常见方法：

1. 优化搜索顺序
   在某些问题中，顺序怎么来枚举都差不多，但对于一些特殊的问题，搜索的顺序会直接影响到整个 DFS 的效率，可见，优化搜索顺序是 DFS 剪枝中的一个常用方法。
2. 排除等效冗余
   简单来讲，就是不搜索重复的结点，比如搜索 $123$ 和搜索 $321$ 是同一个效果（特殊问题除外），一遍都是人为定义一个搜索的顺序，只按照这个顺序搜索下去。因为改变一下顺序搜索对答案的影响是一样的。
3. 可行性剪枝
   如果搜索的当前结点已经无法搜索到答案，那么就没必要往下继续搜索了，则提前返回，这也是 DFS 剪枝中最常用的剪枝。
4. 最优化剪枝
   如果搜索的当前结点不可能作为答案输出，则提前返回，比如再往下搜索对答案的影响都不可能再变小，则直接返回。

　　 同样的，让我们来看一道例题来看看剪枝是怎么应用到题目中的。

　　 题目大意： 给定若干个长木棍和若干的短木棍，让我们从长木棍中裁剪出若干个短木棍，问我们最多可以裁出多少根短木棍。每个长木棍和短木棍只能使用一次。

　　 思路： 数据范围只有 $m\leq50$ 所以直接深搜就行了，但需要加一点剪枝优化。

　　 剪枝 $1$

　　 排序 $+$ 二分

　　 先将长木棍和短木棍从小到大排序。

　　 显然，我们裁的时候一定是从小到大裁剪的前 $k$ 个，不妨设我们裁剪的不是最小的 $k$ 个，那么我们裁剪最小的 $k$ 个，方案数不会变少。

　　 所以只需要裁剪从小到大的前 $k$ 的短木棍就可以了，所以需要存一个短木棍的前缀和 S[i]。

　　 我们还可以发现，如果裁剪的是前 $k$ 个短木棍的话，那么在 $k$ 之前的一定可以裁剪，在 $k$ 之后的一定不能裁剪，所以具有二段性，所以就可以二分了。

　　 剪枝 $2$（优化搜索顺序）

　　 我们在判断前 $k$ 个短木棍能不能裁剪出来的时候，直接搜索就可以了，可以从后往前枚举（即从大到小）短木棍。

　　 从大到小枚举可以使搜索树的分支更少，从而更快的触发剪枝条件。

　　 剪枝 $3$（可行性剪枝）

　　 我们开一个变量 total 来记录所有长木棍的总长度，如果 total < S[k] 那么一定无解。

　　 剪枝 $4$

　　 如果某个长木棍的长度都要 $<$ 最短的木棍的长度的话，那么也一定无解。

　　 剪枝 $5$（排除等效冗余）

1. 如果有几个长度相等的短木棍的话，改变裁剪顺序都是等价的，所以我们可以定一个搜索顺序，避免重复搜索。
2. 如果我们发现有两个相等的长木棍，如果在第一个长木棍无解，那么与它相等的长木棍也一定无解。

　　 完整代码：

#include <iostream>
#include <cstring>
#include <algorithm>

using namespace std;

const int N = 55, M = 2 << 10;

int n, m;
int Board[N];      // 老板提供的每一块木板的长度（长木板）
int board[M];     // 约翰需要的每一块木板的长度（短木板）
int total;              // 长木板的总长度
int sum[M];             // 短木板的前缀和
int mid;


bool dfs(int u, int start)
{
    if (!u) return true;
    if (total < sum[u]) return false; // 剪枝 3
    if (u + 1 > mid || board[u] != board[u + 1]) start = 1;
    
    for (int i = start; i <= n; i ++ )
    {
        if (i > start && Board[i] == Board[i - 1]) continue;  // 剪枝 5.2
        
        if (Board[i] >= board[u])
        {
            total -= board[u], Board[i] -= board[u];
            if (Board[i] < board[1]) total -= Board[i]; // 剪枝 4
            
            if (dfs(u - 1, i))
            {   
                // 由于要回溯，所有需要恢复现场
                if (Board[i] < board[1]) total += Board[i];
                total += board[u], Board[i] += board[u];
                return true;
            }
            
            if (Board[i] < board[1]) total += Board[i];
            total += board[u], Board[i] += board[u];
        }
    }
    
    return false;
}

int main()
{
    cin >> n; 
    for (int i = 1; i <= n; i ++ ) 
        cin >> Board[i], total += Board[i];    // 记录所有长木棍的总长度
    sort(Board + 1, Board + n + 1);
    
    cin >> m;
    for (int i = 1; i <= m; i ++ ) 
        cin >> board[i];
    sort(board + 1, board + m + 1);
    
    // 短木棍的前缀和
    for (int i = 1; i <= m; i ++ ) 
        sum[i] = sum[i - 1] + board[i];
    
    // 二分答案
    int l = 0, r = m;
    while (l < r)
    {
        mid = l + r + 1 >> 1;
        if (dfs(mid, 1)) l = mid;
        else r = mid - 1;
    }
    
    cout << r << endl;
    
    return 0;
}