树与图的深度优先搜索

贡献者：有机物

预备知识　深度优先搜索（DFS），单链表

　　本文将介绍树与图的深度优先搜索。

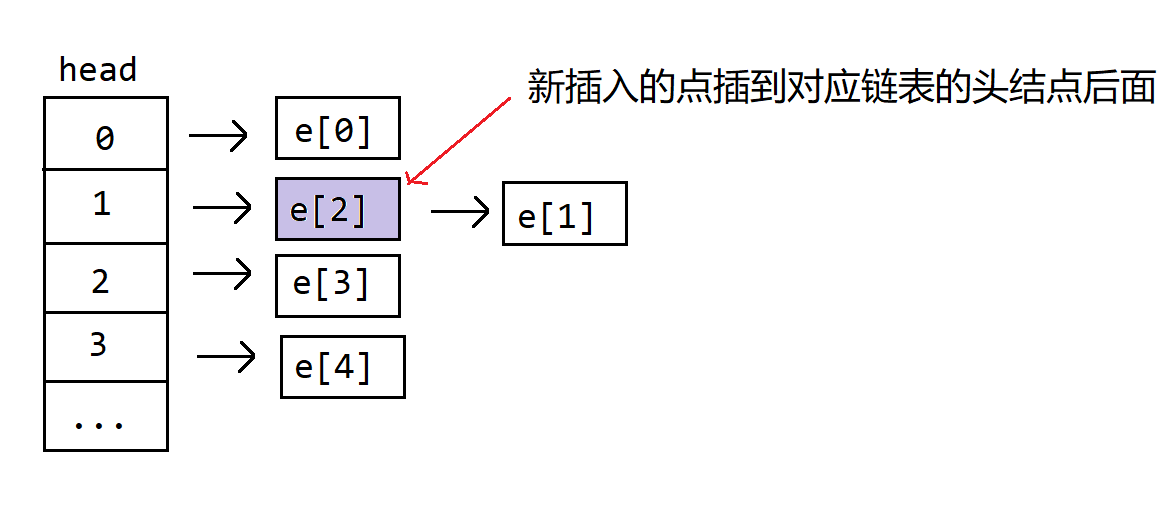
　　 树与图的存储： 存储可以使用邻接表，邻接表的实现可以使用前面学的单链表，邻接表就是 $n$ 个单链表，邻接表的所使用的数组需要多开一个 head 数组，表示每个单链表的表头。邻接表的插入一般都是头插法，即从单链表的表头插入新结点。

图 1：邻接表插入一个数

　　可见，对于一张 $n$ 个点 $m$ 条边的图，可以用 $n$ 个单链表构成， $\forall x \in Graph$ 要想找到 $x$ 的所有出边，可以依据 $x$ 的表头依次访问。

int h[N], e[N], ne[N], idx = 0;

// 在表头是 a 的链表的头结点后面插入一个数 b
void add(int a, int b)
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

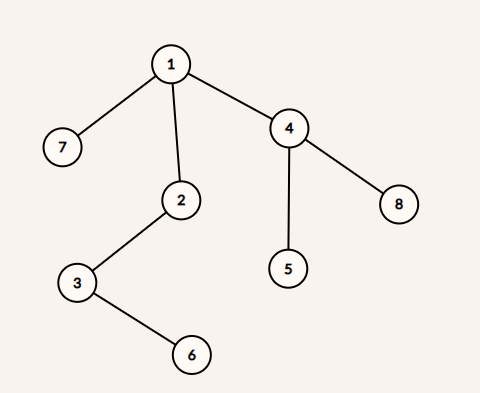
图 2：示例图

const int N = 1e5 + 10, M = N;

int h[N], e[M], ne[M], idx;

void add(int a, int b)  // 添加一条边 a->b
{
    e[idx] = b, ne[idx] = h[a], h[a] = idx ++ ;
}

int main()
{
    int n;  // 结点数
    cin >> n;
    
    memset(h, -1, sizeof h); // 初始化每个单链表的表头
    for (int i = 0; i < n - 1; i ++ )
    {
        int a, b;
        cin >> a >> b;
        // 添加一条无向边 a -- b，等于添加两条有向边 a --> b, b --> a
        add(a, b), add(b, a);  // 建立双向边（无向边）
    }
    
    // 打印邻接表
    for (int i = 1; i <= n - 1; i ++ )  // n - 1 条边
    {
        cout << i << ':';
        for (int j = h[i]; j != -1; j = ne[j])
            cout << "->" << e[j];  // j 为下标，e[j] 就是值
        cout << endl;
    }
    
    return 0;
}

/*
输入：
8
1 4
1 2
1 7
4 8
4 5
2 3
3 6

输出：
1:->7->2->4
2:->3->1
3:->6->2
4:->5->8->1
5:->4
6:->3
7:->1

*/

　　输出的结果就是每个链表的结点的值。

　　图的深度优先遍历就是从根结点开始选择一条边遍历，遍历到当前边的叶结点就回溯，再继续走到别的分支。

void dfs(int x)
{
    st[x] = true;
    for (int i = h[x]; ~i; i = ne[i])
    {
        int j = e[i];  // j 为图中点的编号
        if (!st[j]) dfs(j); // 没被访问过就继续遍历
    }
}

　　树的 DFS 序就是每一个结点在深度优先遍历中进出栈的时间序列，最后序列的长度为 $2 n$ 。树的 DFS 序的特点是，对于一个结点 $x$ ，在序列中会出现两次，那么以这个结点出现的首次和末次的序列就是以这个结点为根的 DFS 序。

void dfs(int x)
{
    a[cnt ++ ] = x;
    st[x] = true; // 标记 x 结点已经被访问
    for (int i = h[x]; ~i; i = ne[i])
    {
        int j = e[i];
        if (!st[j]) dfs(j); // 没被访问过就继续遍历
    }
    
    a[cnt ++ ] = x;
}

dfs(1);   // 调用入口

// 输出 DFS 序
for (int i = 0; i < cnt; i ++ ) cout << a[i] << ' ';

致读者：小时百科一直以来坚持所有内容免费无广告，这导致我们处于严重的亏损状态。长此以往很可能会最终导致我们不得不选择大量广告以及内容付费等。因此，我们请求广大读者热心打赏 ，使网站得以健康发展。如果看到这条信息的每位读者能慷慨打赏 20 元，我们一周就能脱离亏损，并在接下来的一年里向所有读者继续免费提供优质内容。但遗憾的是只有不到 1% 的读者愿意捐款，他们的付出帮助了 99% 的读者免费获取知识，我们在此表示感谢。