库仑定律

                     

贡献者： _Eden_; addis

　　 在 1785 年法国科学家库仑由扭秤实验得到库仑定律，然而其实早在几十年前卡文迪许就通过同心球电荷分布实验得到更精确的结果，其手稿于 1871 年被麦克斯韦所发掘。

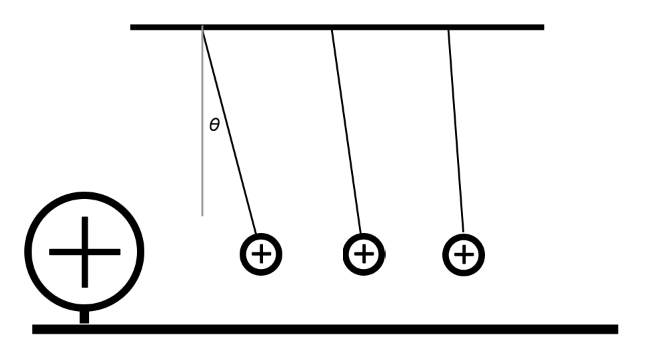
　　 在这里我们只介绍一个简单的可以检验库仑定律的实验。实验装置由一个固定不动的带电钢球 $M$，和一个被细线悬挂的小带电钢球 $A$ 组成。我们将发现，悬挂着小钢球 $A$ 的细线倾斜了一个小角度，偏离了垂直位置一段距离，这意味着 $M$ 似乎对 $A$ 产生了一个排斥力。再用另一个与 $A$ 具有相同材质、大小和形状的小钢球 $B$ 与 $A$ 接触，使得 $B$ 平分了 $A$ 球上的电荷，于是 $A$ 球携带的电荷变为了原来的 $1/2$ 倍。实验现象是：此时钢球 $A$ 偏离垂直位置的距离大约变为了原来的 $1/2$。由此可以总结：两电荷间的静电力是与它们分别所携带的电荷量成正比的。继续进行实验，我们改变钢球 $A$ 悬挂的位置，使得它与 $M$ 的距离变为原来的 $2$ 倍、$3$ 倍、$4$ 倍……实验结果是，$A$ 球偏离垂直位置的距离依次变为原来的 $1/4$ 倍、$1/9$ 倍、$1/16$ 倍。这启发我们得到静电相互作用的平方反比律，即两电荷间的静电力与距离的平方成反比。

1. 库仑定律

　　 真空中两个静止的点电荷间的相互作用被库仑定律所描述。在阐释这个定律之前我们需要先定义点电荷，点电荷就是在质点的基础上（忽略物体的大小与形状），增加了一个总电荷量的属性。这样以后我们的质点往往携带这些物理量 "$ \boldsymbol{\mathbf{r}} =(x,y,z),m,q$" 分别代表它的坐标、质量、电荷量。这些量可能在运动以及相互作用的过程中发生变化，但我们通常假定它的静止质量、它携带的电荷是该质点所不变的属性¹。库仑定律描述了真空中两个静止点电荷间的相互作用力，它的本质不同于引力，却有与引力几乎相同的数学表达形式：它与两个点电荷的电荷量成正比，且与两点电荷的距离的平方成反比。与万有引力的式 1 类似，两个点电荷间的库仑力的矢量表达式为

其中 $ \boldsymbol{\mathbf{F}} _{1,2}$ 表示点电荷 $2$ 所受到的力的大小，$\hat{ \boldsymbol{\mathbf{r}} }_{12}$ 表示从 $1$ 指向 $2$ 的单位矢量。$q_1, q_2$ 分别是两个点电荷的电荷量。注意比起万有引力的式 1 ，式 1 没有负号，$q_1, q_2$ 可以是负数（代表负电荷）。当它们同号时 $ \boldsymbol{\mathbf{F}} _{12}$ 是由 $1$ 指向 $2$ 的矢量，而当它们异号时 $ \boldsymbol{\mathbf{F}} _{12}$ 则是从 $2$ 指向 $1$ 的矢量。我们容易看出两电荷同号相斥，异号相吸。

　　 $k$ 是库仑常数，可以在实验中测量；我们也常常将这个符号替换为

$\epsilon_0=8.854\cdot 10^{-12} \,\mathrm{C^2/Nm^2} $ 是真空中的电介质常数（vacuum permittivity），这将在我们之后的学习过程中经常出现；而上式中 $4\pi$ 的出现将使得我们将用到的 “高斯定律” 具有更加简洁的形式。这里我们采取的是 SI 单位制（国际单位制），而描述电磁相互作用力实际上还有许多其他单位制，在不同的场合中经常被使用。

　　 我们将发现，两电子间的库仑力要远远大于它们之间的引力。

2. 局限性

　　 库仑定律实际上存在着许多缺陷。例如点电荷这一理想经典模型往往无法真正地去刻画真实世界。它或许能近似的描述质子、电子或其他带电粒子，但也仅限于两粒子间隔较大的情况，否则这些粒子的内部结构将对粒子间作用力造成影响。现代物理表明，电子是有内禀自旋的，并且是自然界的基本粒子。而质子、中子的结构则要复杂的多，人们认为它们由夸克组成，而这些夸克又是无法被单独分离出来的。这些就远远地超出了我们目前所讨论的知识范畴。但是可以预见，粒子的复杂内部结构将导致带电粒子间相互作用比预想的更加复杂，我们通过库仑定律得到的结果仅仅是非相对论极限下的一个近似。当两粒子以足够高的能量、足够高的速度对撞时，它们之间的距离就能够足够的小，以至于粒子不再能够视为点电荷，经典模型也就不再适用了，而正是通过这样的高能碰撞实验，人们才发现了许多新的物理现象，总结出新的物理规律。

　　 库仑定律的另一缺陷则是，它只能够描述两个静止的粒子间的静电相互作用。对于两个运动的带电粒子，它们之间的库仑相互作用如何，我们目前是不清楚的。在今后的学习中，我们将认识到一些重要的事实：真空中如果有一个静止点电荷 $Q$ 和一个运动的带电荷 $q$ 的测试粒子，那么测试粒子 $q$ 所受到的电磁力仍然可以由库仑定律式 1 给出。然而，如果点电荷 $Q$ 也在运动，则测试粒子 $q$ 还会受到磁场的影响。其更内在的物理原理是：在由 $Q$ 的静止参考系到运动参考系的洛伦兹变换下，电场和磁场会相伴出现。也就是说，电与磁是统一的。

---

1. ^ 除非多个质点间发生了碰撞，则此时我们需要重新对质点在碰撞前后的变化进行定义，使之符合我们的实验现象。