广度优先搜索（BFS）

贡献者： 有机物

　　 上文提到了 DFS，本文将介绍与它类似的一种搜索方式：广度优先搜索或者叫宽度优先搜索（Breadth First Search）简称 BFS。

　　 BFS 可以用队列来实现，BFS 的搜索顺序为：当前的状态面临的所有状态优先搜索。

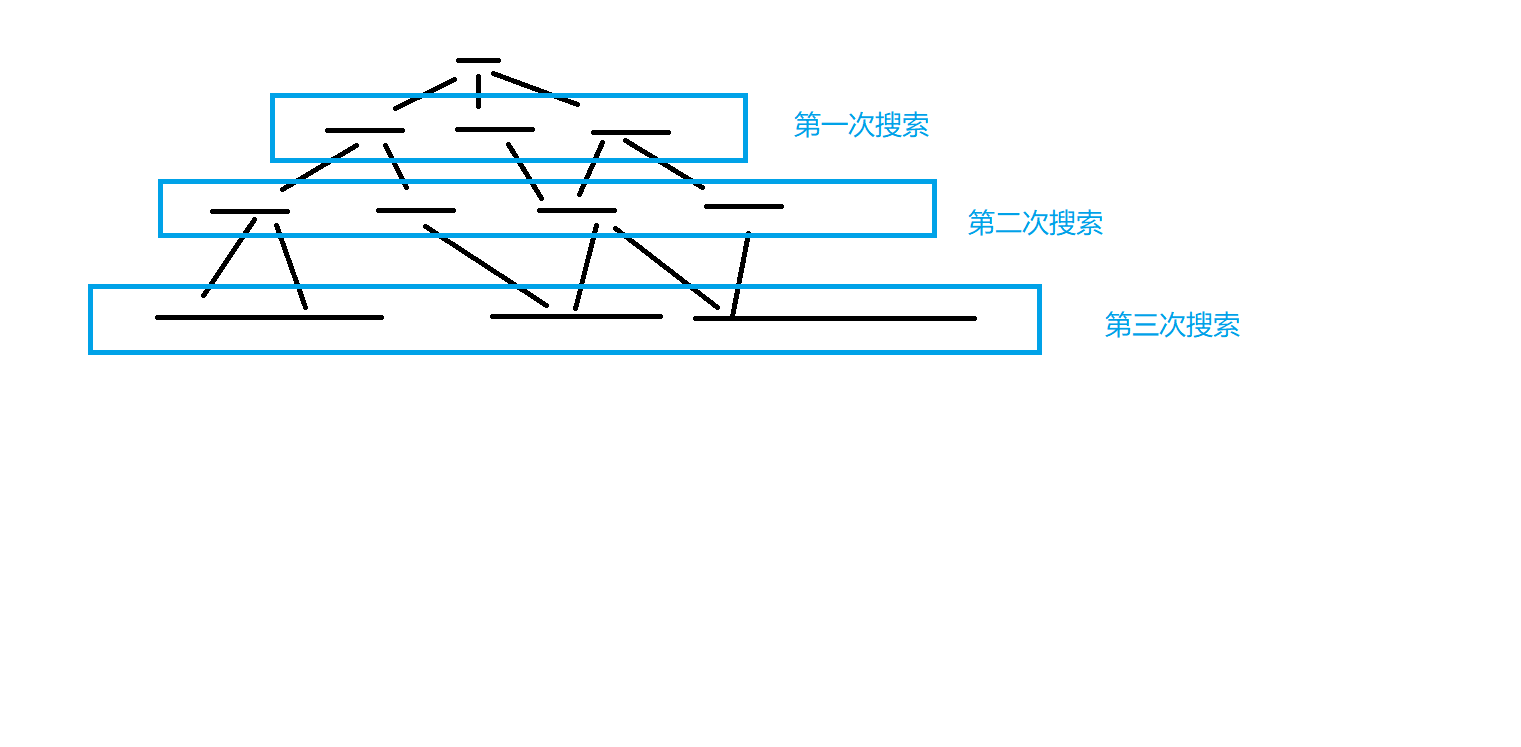
　　 对于一棵搜索树，BFS 不是一个节点一个节点的搜索，而是一层一层的搜索，如果当一个状态第一次入队的时候，那么就是从起始状态到该状态的最小步数，因此 BFS 可以求最小值。对于一张权值都为 $1$ 的图，可以求得从 $1$ 号点到 $n$ 号点的最短距离。

　　 BFS 的伪代码：

while (队列不空) 
{
    t <--队头
    从队头更新其他节点
}

　　 我们还是看一道例题来学习 BFS：

　　 题意：有一张地图，$0$ 表示可以走，$1$ 表示不能走，你可以从上下左右四个方向任意一个方向移动一个位置，问你从 $1,1$ 走到 $n,n$ 最少需要花费多少步？

　　 样例：

输入：
5 5
0 1 0 0 0
0 1 0 1 0
0 0 0 0 0
0 1 1 1 0
0 0 0 1 0

输出：
8

　　 思路：

　　 上图就为 BFS 的搜索顺序，每次搜索队头可以到达的点，然后根据队头更新信息，可以保证答案一定是最小值。先把 $0$ 号点入队，然后把 $0$ 号点出队，然后访问队头（$0$ 号点）的可以到达的节点，然后在把队头可以到达的节点入队，可以到达的节点的答案为从起点到队头的答案再加从队头到可以到达的节点的步数也就是直接加 $1$。

　　 代码：

const int N = 110;

typedef pair<int, int> PII;

int n, m, d[N][N], g[N][N]; // d 为每个点的距离，g 为地图
PII q[N * N];   // q 数组为数组模拟队列，因为是二元组，所以要开二倍空间

bool check(int x, int y)
{
    // 如果越界了或者当前遇到了不可通过的墙壁或者访问到了更新过的节点，就直接返回
    if (x < 0 || x >= n || y < 0 || y >= m || d[x][y] != -1 || g[x][y] == 1) 
        return false;
    return true;
}

int bfs()
{
    // 数组模拟队列
    int hh = 0, tt = -1;
    q[ ++ tt] = {0, 0};     // 最开始起点入队
    memset(d, -1, sizeof d);    // 初始化所有的点都还没被更新过
    d[0][0] = 0;    // 起点的距离为 1
    
    int dx[4] = {-1, 0, 1, 0};  // x 轴的偏移量
    int dy[4] = {0, 1, 0, -1};  // y 轴的偏移量
    
    while (hh <= tt)    // 队列不为空
    {
        auto t = q[hh ++ ];     // 取出队头并把队头出队
        for (int i = 0; i < 4; i ++ )   // 枚举上下左右 4 个方向
        {
            // a、b 为从队头往上下左右四个方向之一走下去点
            int a = t.first + dx[i], b = t.second + dy[i];   
            if (!check(a, b)) continue;     // 如果下一个点不满足条件的话就往下一个方向走
            q[ ++ tt] = {a, b}; // 把走过的点加入队头
            d[a][b] = d[t.first][t.second] + 1;  // 更新距离
        }
    }
    
    return d[n - 1][m - 1]; // 返回从 1 号点走到 (n, m) 的距离
}

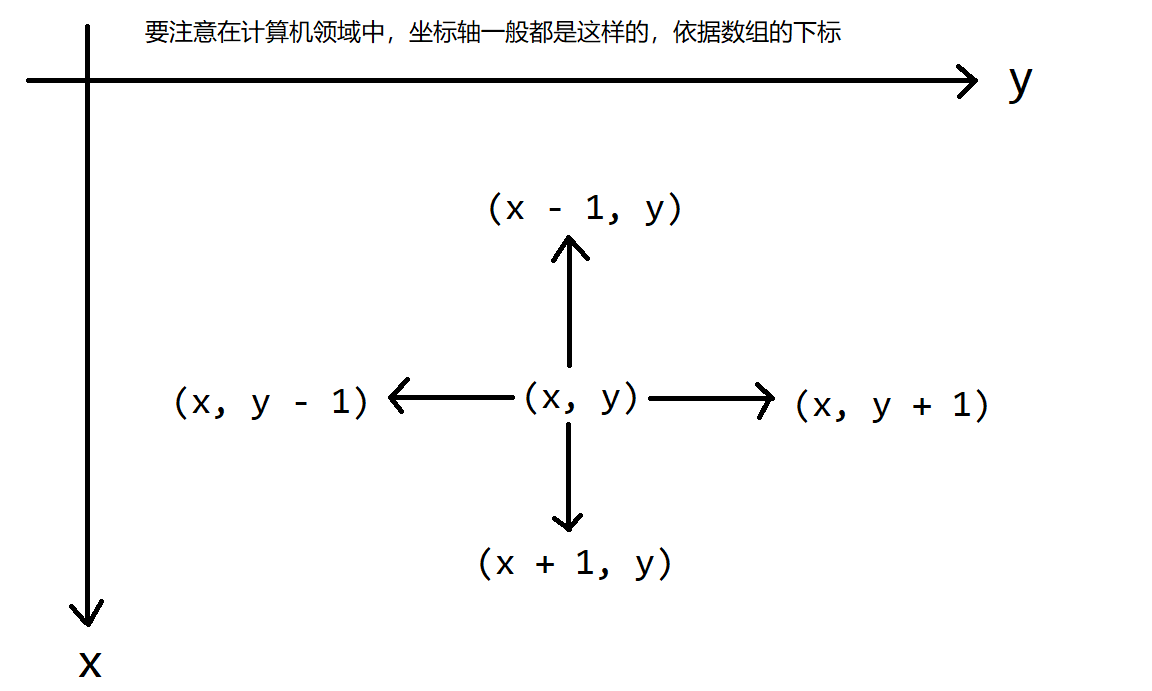
　　 可以看到，对于涉及到上下左右方向类的问题，可以不需要写 $4$ 个 if 判断，我们直接使用两个偏移量，这样可以帮助我们省很多代码。

1. 往上走就是横坐标减 $1$，纵坐标不变。对应：$\mathtt{-1, 0}$
2. 往右走就是横坐标不变，纵坐标加 $1$。对应：$\mathtt{0, 1}$
3. 往下走就是横坐标加 $1$，纵坐标不变。对应：$\mathtt{1, 0}$
4. 往左走就是横坐标不变，纵坐标减 $1$。对应：$\mathtt{0, -1}$

　　 让我们来看一道使用偏移量的好题：例题

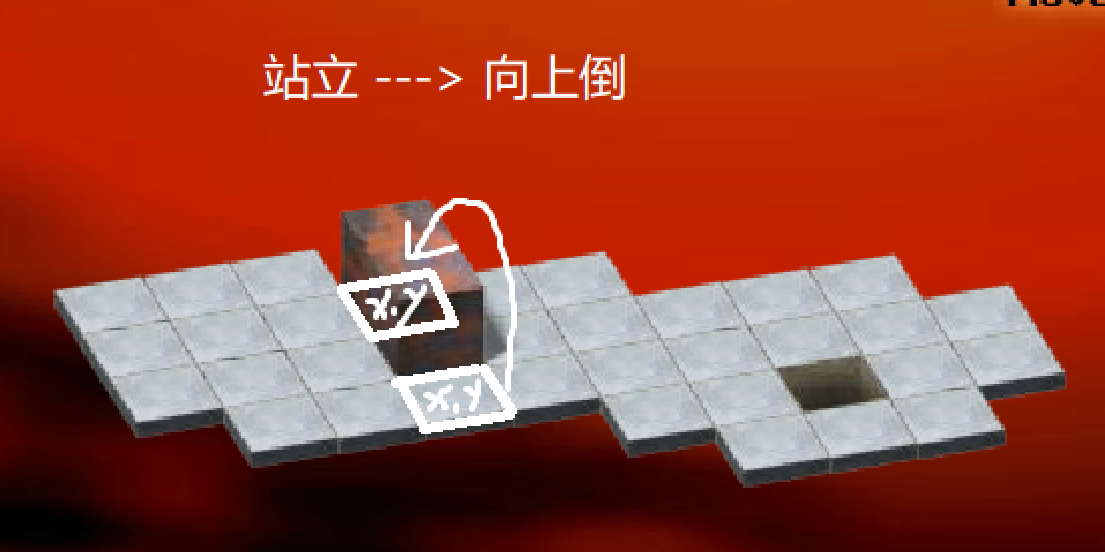
　　 题目大意：控制一个 $1 \times 1 \times 2$ 小木块，问从起点走到终点最少需要操作多少次，“。” 表示硬地，可以躺着也可以站立着，“E” 表示脆地，只能躺着，“#” 表示障碍物，不能通过。游戏地址。 本题和这款游戏有的操作一模一样，偏移量的值可以根据里面的操作来判断。

　　 做法：

　　 用一个结构体来定义状态，结构体内有三个值，分别为：$\mathtt{x, y, lie}$。$\mathtt{lie}$ 为当前小木块的状态，$0$ 表示竖着站立在 $\mathtt{x, y}$ 上、$1$ 表示横着躺，左半部分为 $\mathtt{x, y}$、$2$ 表示竖着躺，上半部分为 $\mathtt{x, y}$。

　　 本题的偏移量：

int d[3][4][3] = {
    {{-2, 0, 2}, {0, 1, 1}, {1, 0, 2}, {0, -2, 1}},  
    {{-1, 0, 1}, {0, 2, 0}, {1, 0, 1}, {0, -1, 0}},  
    {{-1, 0, 0}, {0, 1, 2}, {2, 0, 0}, {0, -1, 2}},  
};

　　 d 数组的第一维（对应上面的行）表示当前的状态是什么，为 $1$ 表示最开始是立着的、为 $2$ 表示最开始是横着躺、为 $3$ 表示最开始是竖着躺。 第二维（对应上面的四大列）表示四个方向，第一大列表示向 “上” 走，第二大列表示向 “右” 走，第三大列表示向 “下” 走，第四大列表示向 “左” 走。 第三维则代表每行内的四个花括号内的元素，第一个元素表示 $x$ 轴，第二个元素表示是 $y$ 轴，第三个元素表示状态。

　　 上面的偏移量的更新可以去依据那个游戏，本题的思路较简单，重点就在于上面的偏移量技巧。

　　 代码：

#include <iostream>
#include <cstring>
#include <algorithm>
#include <queue>

using namespace std;

const int N = 510;

struct State
{
    int x, y, lie;
};

int n, m;
char g[N][N];
int dist[N][N][3];
// 数组模拟队列
State q[N * N * 3]; // 因为有 3 个状态，所有数组要开 3 倍大小

bool check(int x, int y)
{
    if (x < 0 || x >= n || y < 0 || y >= m) return false;
    return g[x][y] != '#';
}

int bfs(State, State);  // 先声明一下 BFS 函数

// 处理起点和输出答案
void process(int x, int y)
{
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < m; j ++ )
            cin >> g[i][j];
    
    State start = {-1, -1, -1}, end;
    for (int i = 0; i < n; i ++ )
        for (int j = 0; j < m; j ++ )
            if (g[i][j] == 'X')
            {
                if (start.x != -1) continue;    // x 必须是第一次找到的
                // 86 行注释：如果 x,y 这个点左边的点也是 X，说明最开始的状态是横向躺着的
                if (g[i][j + 1] == 'X') start = {i, j, 1};
                // 88 行注释：如果 x,y 这个点下边的点也是 X，说明最开始的状态是竖向躺着的
                else if (g[i + 1][j] == 'X') start = {i, j, 2};
                else start = {i, j, 0}; // 说明起点是站立的
            }
            // 92 行注释：找到了终点，终点的状态只能是立着的，即为 0
            else if (g[i][j] == 'O') end = {i, j, 0};   
    
    int res = bfs(start, end);  // 从起点开始搜
    if (~res) cout << res << endl;
    else cout << "Impossible" << endl;

}

int bfs(State start, State end)
{
    // 59 行注释：先把距离都初始化为 -1，表示所有点都没被访问和更新
    memset(dist, -1, sizeof dist);  
    dist[start.x][start.y][start.lie] = 0;  // 起点的距离为 0
    int hh = 0, tt = -1;
    q[ ++ tt] = {start};    // 先把起点入队
    
    
    // 3 行 4 列共有 3 个元素
        // 上          右          下       左
    int d[3][4][3] = {
        {{-2, 0, 2}, {0, 1, 1}, {1, 0, 2}, {0, -2, 1}},  
        {{-1, 0, 1}, {0, 2, 0}, {1, 0, 1}, {0, -1, 0}},  
        {{-1, 0, 0}, {0, 1, 2}, {2, 0, 0}, {0, -1, 2}},  
    };
    
    while (hh <= tt)
    {
        auto t = q[hh ++ ]; // 取出队头
        
        // 拓展 t
        for (int i = 0; i < 4; i ++ )   // 拓展4个方向
        {
            State next;
            next = {
                t.x + d[t.lie][i][0],
                t.y + d[t.lie][i][1],
                d[t.lie][i][2], 
            };
            
            int x = next.x, y = next.y;
            
            if (!check(x, y)) continue; // 不满足条件
            
            // 木块的 3 个状态，判断是否满足条件
            if (next.lie == 0 && g[x][y] == 'E') continue;  
            if (next.lie == 1 && !check(x, y + 1)) continue;
            if (next.lie == 2 && !check(x + 1, y)) continue;
            
            // 尚未被更新
            if (dist[x][y][next.lie] == -1)
            {
                dist[x][y][next.lie] = dist[t.x][t.y][t.lie] + 1;
                q[ ++ tt] = {next};
            }
        }
    }
    
    return dist[end.x][end.y][end.lie];
}

int main()
{
    while (scanf("%d%d", &n, &m), n || m) process(n, m);
    
    return 0;
}