线段树

贡献者： 有机物; addis

　　 线段树（Segment tree）是一种二叉树形的数据结构，用以存储区间或线段，并且可以在 $O(\log N)$ 的时间复杂度查询区间最大值、最小值、总和等属性。

　　 线段树的存储：

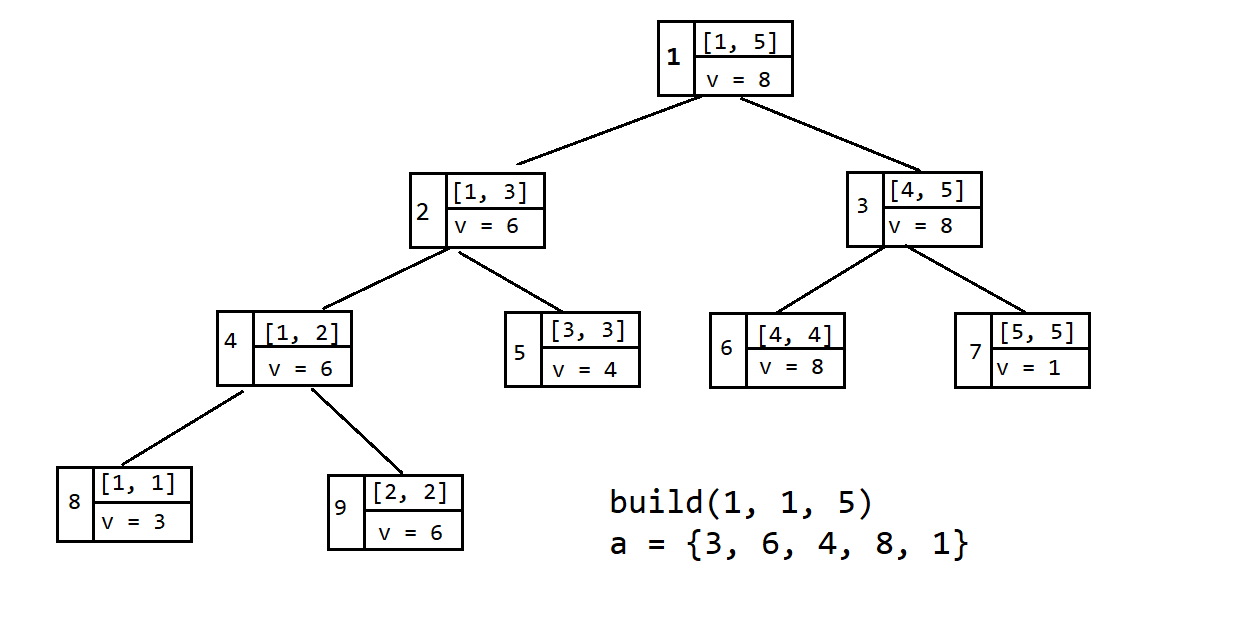
　　 线段树除了最后一层节点外是一棵满二叉树，因此可以用堆的存储方式来存储线段树。 具体来说就是开一个一维数组，根节点的编号为 $1$，编号为 $x$ 的结点的左子节点的编号为 $x \times 2$，右子节点的编号为：$x \times 2 + 1$，父节点的编号为 $\left\lfloor\dfrac{x}{2}\right\rfloor$。

　　 因此我们可以用一个结构体来存储线段树，线段树除了最后一层结点外是一棵满二叉树，除了最后一层结点外的结点个数为：$N + \dfrac{N}{2} + \dfrac{N}{4} + \cdots + 2 + 1 = 2N - 1$，最后一层的结点个数最坏情况下是 $2N$ 个结点，所以数组大小应不小于 $4N$ 才能保持不越界。

　　 可以看出，线段树的每个结点都代表一个区间，叶结点的区间长度都为 $1$，对于每个区间结点 $[l, r]$，左子结点为 $[l, mid]$，右子结点为 $[mid + 1, r]$，$mid = \left\lfloor\dfrac{l+r}{2}\right\rfloor$。

　　 线段树的建树（$\texttt{build}$）操作：

　　 一般来说，线段树每个结点上存储了很多信息，具体存什么信息得根据具体情况判断，这里以存储区间最大值为例，我们用递归来建树，每个叶结点 $[i, i]$ 保存 $a_i$ 的值，每次递归左子节点和右子节点，最后根据子节点的信息更新当前结点的信息，这一操作称为 $\text{pushup}$ 操作。

struct Node {
    int l, r, v;  // v 代表区间最大值
}tr[4 * N];

void build(int u, int l, int r) 
{
    tr[u] = {l, r};
    
    if (l == r) // 叶节点
    {
        tr[u] = {l, r, a[l]};  // 也可只写 tr[u].v = a[l];
        return;
    }
    
    int mid = l + r >> 1;
    build(u << 1, l, mid);          // 左子节点[l, mid]，编号为：u << 1
    build(u << 1 | 1, mid + 1, r);  // 右子节点[mid + 1, r]，编号为：u << 1 | 1
    pushup(u);
}

build(1, 1, n);   // 调用建树，从根节点开始

　　 线段树的 $\texttt{pushup}$ 操作：

　　 线段树可以很容易的把左右两个子结点的信息上传到当前结点，所以在记录每个结点 $i$ 的最大值就可以用左子节点 $\mathtt{i<<1}$ 的最大值和右子节点 $\mathtt{i<<1|1}$ 的最大值两者取一个最大值就是当前结点 $i$ 的最大值。

void pushup(int u)
{
    tr[u].v = max(tr[u << 1].v, tr[u << 1 | 1].v);
}

　　 线段树的单点修改（$\texttt{modify}$）操作：

　　 单点修改操作一般是把 $a[x]$ 的值修改成 $v$，我们从根结点开始，递归左右两个子节点，找到 $[x, x]$ 区间，然后从下往上把对应的父节点保存的最大值进行更新。

void modify(int u, int x, int v)    // 把 a[x] 修改为 v
{
    if (tr[u].l == x && tr[u].r == x) tr[u].v = v;  // 叶节点
    else
    {
        int mid = tr[u].l + tr[u].r >> 1;       // mid 为树中区间的 mid
        if (x <= mid) modify(u << 1, x, v);     // x 属于左半区间
        else modify(u << 1 | 1, x, v);          // x 属于右半区间
        pushup(u);  // 记得更新父节点的值
    }
}

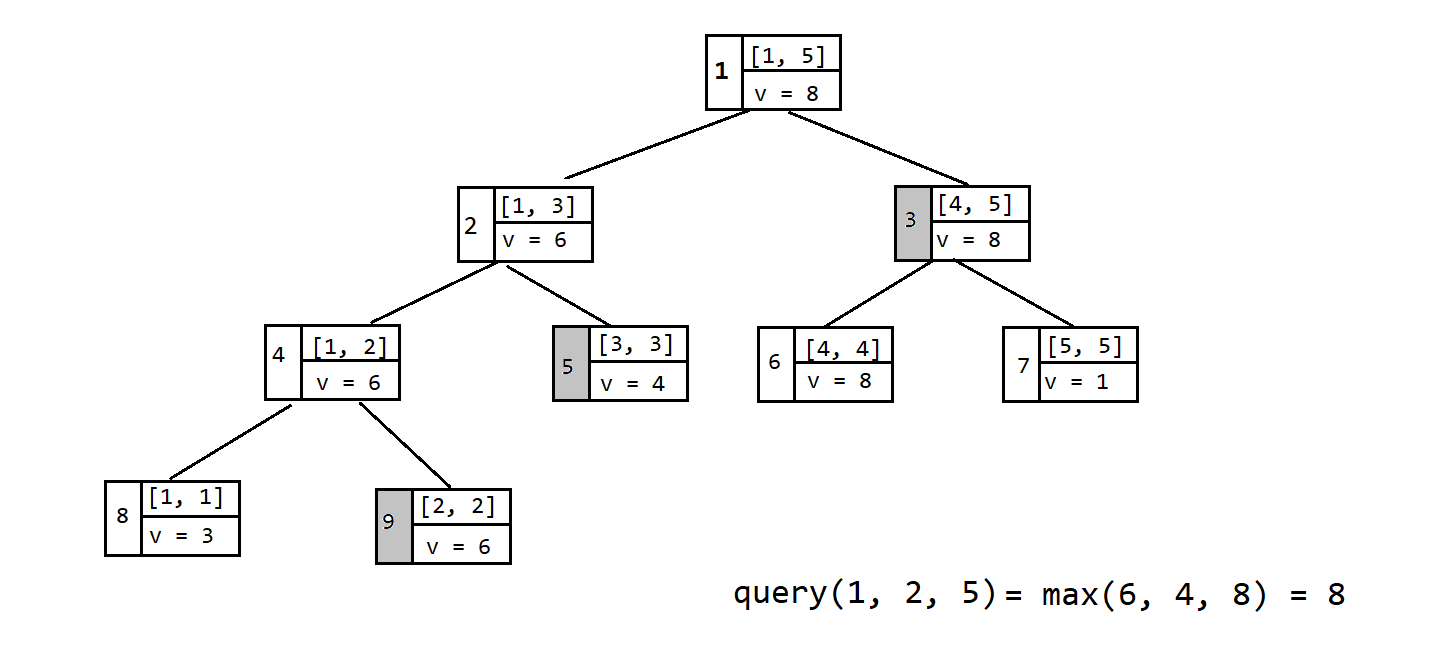
　　 线段树的区间查询（$\texttt{query}$）操作：

　　 查询操作一般为查询某个区间的某种属性，例如查询区间 $[l. r]$ 内的最大值。我们只需要从根节点开始递归查询，会出现如下几种情况：

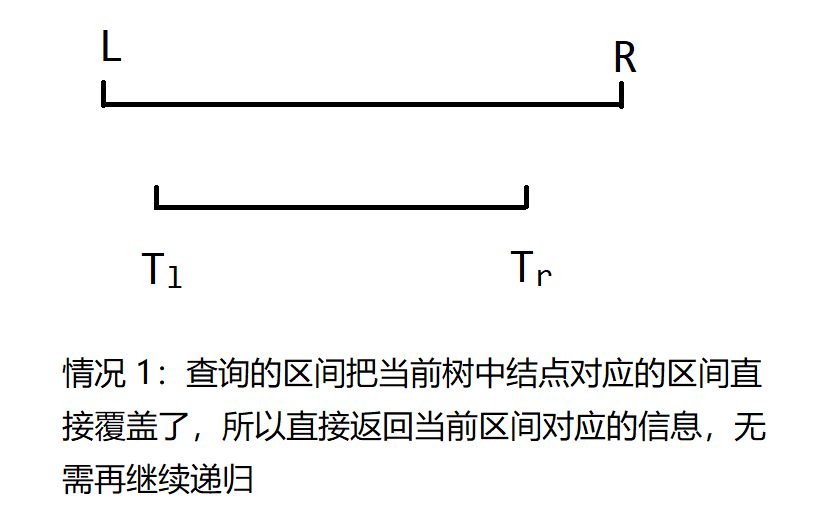
1. 查询的区间 $[l, r]$ 完全包含了当前结点的代表区间，则直接返回该区间的最大值，因为没必要再递归查询下去了。
2. 查询的区间 $[l, r]$ 与左子节点有交集，则递归查询左子节点
3. 查询的区间 $[l, r]$ 与右子节点有交集，则递归查询右子节点

　　 查询操作会把询问的区间 $[l, r]$ 分成 $\log N$ 个区间，来简单的证明一下： 在递归每个树上的结点 $[T_l, T_r]$ 时，$mid = \left\lfloor\dfrac{T_l+T_r}{2}\right\rfloor$ 会出现以下几种情况：

1. $l \leq T_l \leq T_r \leq r$ 即当前树中结点对应的区间完全在查询区间的内部
2. $T_l \leq l \leq T_r \leq r$ 即只有 $l$ 与当前树中结点对应的区间有交集
   (1) $l > mid$，$l$ 只与当前树中结点对应的区间的右半部分 $[mid + 1, r]$ 有交集；
   (2) $l \leq mid$，$l$ 与当前树中结点对应的区间的左右两边都有交集，需要递归左右两边，但是递归的右子结点会在递归后直接返回，即触发了情况 $1$.
   
3. $l \leq T_l \leq r \leq T_r$ 即只有 $r$ 与当前树中结点对应的区间有交集，对应情况 $2$。
4. $T_l \leq l \leq r \leq T_r$ 即查询区间完全在当前树中结点对应的区间内部。
   (1) $l > mid$ 时只会递归右子结点；
   (2) $r < mid$ 时只会递归左子节点；
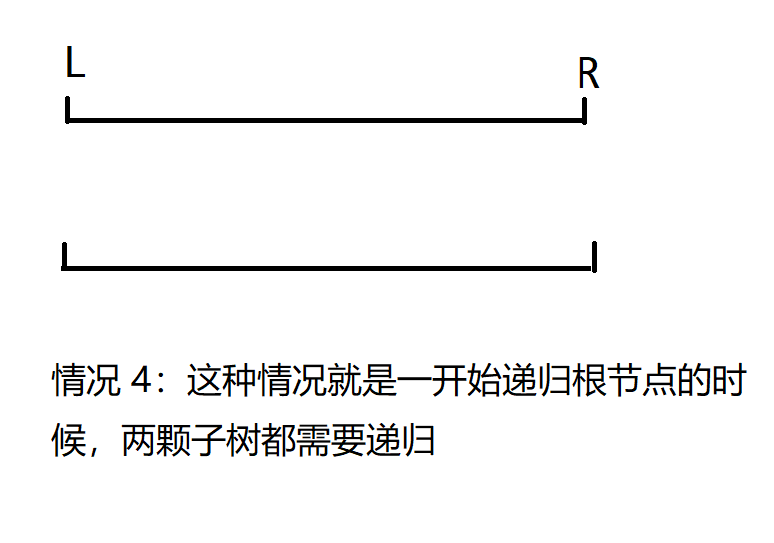
   (3) $l$、$r$ 都与当前树中结点对应的区间有交集，此时需要递归左右子结点。
   

　　 只有 $4(3)$ 这种情况会对线段树的左右两棵子树递归，但这种操作至多发生一次，也就是最开始递归根结点，然后就变成了前三种情况。

int query(int u, int l, int r)
{
    // 完全包含
    if (tr[u].l >= l && tr[u].r <= r) return tr[u].v;  
    
    int mid = tr[u].l + tr[u].r >> 1;
    int v = 0;
    if (l <= mid) v = query(u << 1, l, r);
    if (r > mid) v = max(v, query(u << 1 | 1, l, r));
    
    return v;
}

　　 以上就是线段树的基本操作。

　　 例题：GSS 3

　　 题目大意：

　　 给定长度为 $N$ 的数列 $A$，以及 $M$ 条指令，每条指令可能是以下两种之一：

　　 1. 1 x y，查询区间 $[x,y]$ 中的最大连续子段和，即 $\max\limits_{x \le l \le r \le y}${$\sum\limits^r_{i=l} A[i]$}。

　　 2. 2 x y，把 $A[x]$ 改成 $y$。

　　 对于每个查询指令，输出一个整数表示答案。

　　 本题因为要求最大连续子段和，首先考虑一下线段树要存什么信息。肯定要存一个最大连续子段和 $\tt tmax$。那父节点的最大连续子段和能否由子节点更新得来呢？答案是不行的，因为当父节点的最大连续子段和是横跨左右子节点的时候，不能由子节点直接更新得来。

　　 所以还需存左子节点的最大后缀和 $\tt rmax$ 以及右子节点的最大前缀和 $\tt lmax$。所以由子节点向父节点更新的最大连续子段和只有三种情况：

1. 左子节点的最大连续子段和 $\tt l.tmax$。
2. 右子节点的最大连续子段和 $\tt r.tmax$。
3. 左子节点的最大后缀和 $\tt l.rmax$ 加右子节点的最大前缀和 $\tt r.lmax$。

　　 所以父节点 $u$ 的最大连续子段和为：$\texttt{u.tmax = max(l.tmax, r.tmax, l.rmax + r.lmax)}$。

　　 那么父节点的最大前/后缀和能否由子节点的最大前/后缀和更新呢？还是不行，因为当父节点的最大前缀和横跨左右两个子节点的时候，不能只由单个子节点更新。

　　 所以父节点的最大前缀和有两种情况：

1. 左子节点的最大前缀和 $\tt l.lmax$
2. 左子节点的和 $\sum\limits^{\tt mid}_{i = l}a_i$ 加右子节点的最大前缀和 $\tt r.lmax$。

　　 所以还需维护一个区间和 $\tt sum$ 用于计算当前区间的所有元素之和。

　　 后缀和同理。

const int N = 500010;
struct Node
{
    int l, r, lmax, rmax, tmax, sum;
}tr[N * 4];
int n, m, a[N];

void pushup(Node &u, Node &l, Node &r)
{
    u.sum = l.sum + r.sum;
    u.lmax = max(l.lmax, l.sum + r.lmax);
    u.rmax = max(r.rmax, r.sum + l.rmax);
    u.tmax = max(max(l.tmax, r.tmax), l.rmax + r.lmax);
}

void pushup(int u)
{
    pushup(tr[u], tr[u << 1], tr[u << 1 | 1]);
}

　　 修改与建树操作较简单，着重分析一下查询操作。

　　 查询操作肯定是要返回一个区间的最大连续子段和，但是如果查询的区间横跨树中左右子节点，就需要先递归求左子节点的最大连续子段和，再递归求一下右子节点的最大连续子段和，再利用 $\tt pushup$ 操作合并答案。因为父节点的 $\tt tmax$ 不只是由左右子节点的 $\tt tmax$ 两者取最大值，还有可能横跨区间计算，所以需要分情况讨论。

Node find(int u, int l, int r)
{
    if (tr[u].l >= l && tr[u].r <= r) return tr[u];
    else 
    {
        int mid = tr[u].l + tr[u].r >> 1;
        // 查询的区间完全在树中节点对应的区间的左半边
        if (r <= mid) return find(u << 1, l, r);    
        // 查询的区间完全在树中节点对应的区间的右半边
        else if (l > mid) return find(u << 1 | 1, l, r);
        // 查询的区间在树中节点对应的区间的左右两边
        else 
        {
            auto left = find(u << 1, l, r);
            auto right = find(u << 1 | 1, l, r);
            Node res;
            pushup(res, left, right);
            return res;
        }
    }
}

　　 以上讲的线段树的操作只涉及到了单点修改，那如果想要进行区间修改该怎么做呢？如果直接暴力修改，则单次修改的时间复杂度最坏为 $\mathcal{O}(n)$，时间复杂度太高。并且如果修改的区间后续根本没被查询，那么完全没有必要修改这些区间。

　　 可以像区间查询那样，如果树中区间已经被查询区间完全包含了，直接返回，前面证明了查询的时间复杂度为 $\mathcal{O}(\log_2 n)$，但还要在回溯之前在当前区间内加一个延迟标记（懒标记）：“表示当前区间已被修改，但子区间还未被更新”，只有在后续查询或者更新区间的时候，如果涉及到了这个区间，就往下面的两个子结点下传标记，并且清除当前这个区间的标记。

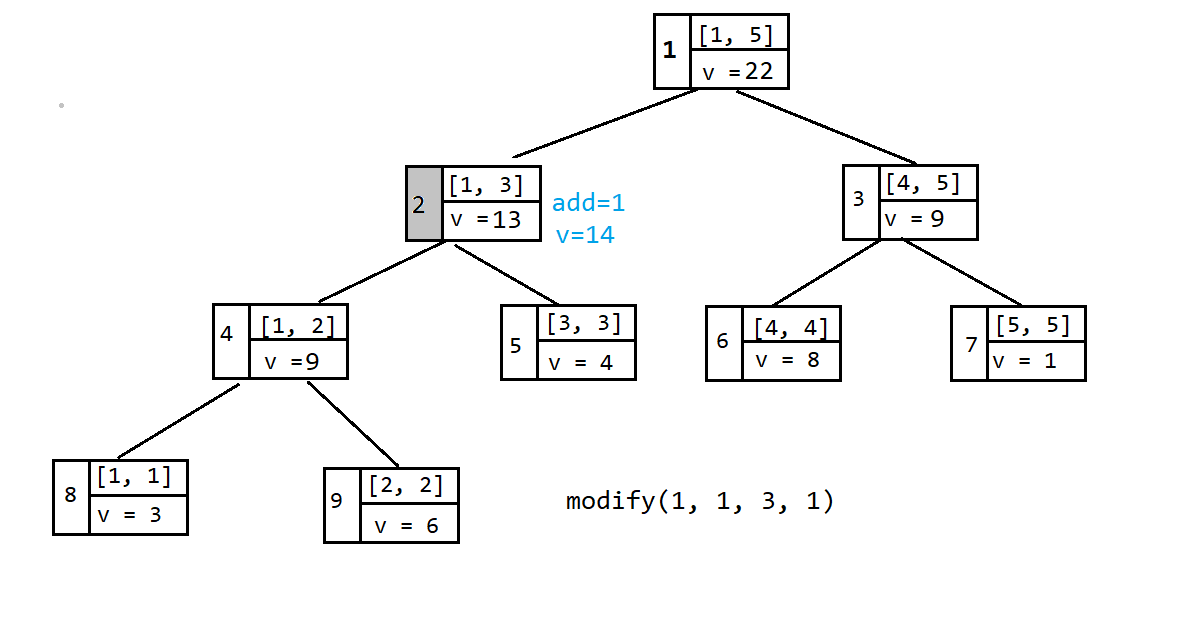
　　 如上图，若要给 $[1, 3]$ 这个区间都加一，这个树中结点正好被查询区间完全包含，给这个节点打一个延迟标记 $\texttt{add = 1}$，并且更新这个节点的值 $\texttt{v = 14}$。

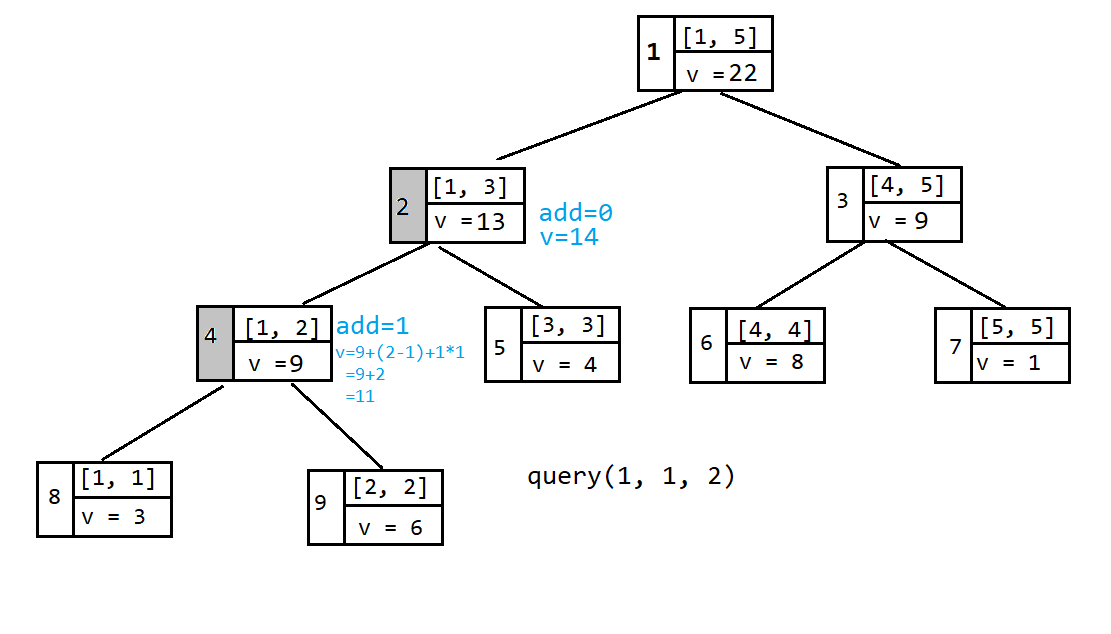
　　 查询区间 $[1, 2]$ 的和，第一次递归到 $[1, 3]$ 这个区间的时候，发现这个区间有标记，则将标记下传到左右两个子节点（右子节点没画出来），然后更新左右两个子节点的值。

　　 所以可以很容易的写出延迟标记 $\tt pushdown$ 的代码：

#define lson u << 1
#define rson u << 1 | 1

void pushdown(int u)
{
    if (tr[u].add)  // 如果节点 u 有标记
    {
        tr[lson].add += tr[u].add;    // 更新左子节点的延迟标记
        // 更新左子节点的值
        tr[lson].sum += (1ll * tr[lson].r - tr[lson].l + 1) * tr[u].add; 
        
        tr[rson].add += tr[u].add;
        tr[rson].sum += (1ll * tr[rson].r - tr[rson].l + 1) * tr[u].add;
        
        tr[u].add = 0;  // 清除当前结点的延迟标记
    }
}