贡献者: _Eden_
1951 年珀塞耳(Purcell)和庞德(Pound)发现氟化锂(LiF)晶体中的核自旋系统可以处于负绝对温度状态。
1956 年喇姆塞(Ramsey)给予了理论解释。[1]
这里的温度在统计力学中的严格意义是式 5
\begin{equation}
\frac{1}{T}=\left(\frac{ \,\mathrm{d}{S} }{ \,\mathrm{d}{E} }\right)_{V,N}^{-1}~.
\end{equation}
有时也将 $E$ 记做 $U$,这都是些符号上的不同使用习惯。在一般系统中,熵随内能的增大而增大(直观的理解就是,系统越热,就越 “乱”)。但也存在一些特殊的系统,它们的熵在特定温度范围内随内能的升高而减小,此时由上式得出的温度就是负的。
1. 理论简介
设核自旋量子数为 $j=\frac{1}{2}$,在外磁场中,核磁矩 $\mu$ 相对于外磁场 $H$ 只有平行和反平行两种取向。相应的能量也只有两种取值:$\epsilon_1=-\mu H,\quad \epsilon_2=\mu H$。假设每个能级只有一个量子态(简并度 $g_1=g_2=1$)。由于核自旋彼此之间相互作用很弱,它们组成了近独立的定域子系。
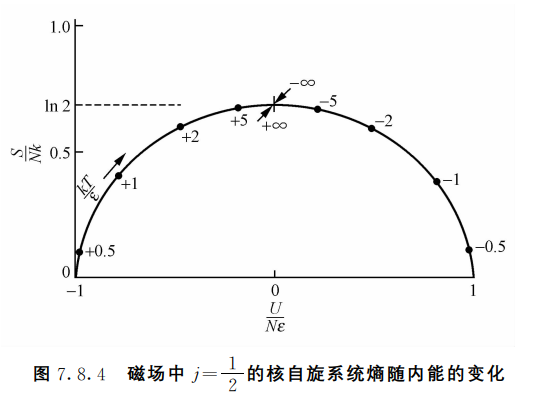
设系统的平均能量为 $\bar{E}=N_1\epsilon_1+N_2\epsilon_2=\mu H(N_2-N_1),\ N_1+N_2=N$,当 $N_1=N$ 时所有磁矩都与外磁场方向平行,系统处于能量最低的有序状态;当 $N_2=N$ 时所有磁矩都与外磁场反平行,系统处于能量罪高的有序状态。可以想象随着能量的增大,核自旋系统从有序到无序再转变为有序。根据玻尔兹曼熵公式1,$S=k\ln \Omega$,因此我们可以预见系统的熵随能量的变化曲线是先增大后减小的。
那么根据式 1 ,随着系统的能量增加,温度 $T$ 先是从 $0$ 增加到 $+\infty$,此时熵函数达到最高点;继续增加能量,温度跳变到 $-\infty$,并从 $-\infty$ 逐渐增加到 $0$,在这个过程中出现了负温度。
负温度比 $0 \mathrm{K}$ 低这种说法是不准确的,因为我们从上面的讨论中看到,实际上负温度比一切的正温度都要 “热”。在热力学第一定律 成立的情况下,如果我们将负温度的系统与正温度的系统靠在一起,热量总是从负温度的系统传向正温度的系统;在这一过程中,正温度的系统内能增加,负温度的系统内能减小,两个系统的熵都是在增加的;事实上在后面我们将看到,热力学第二定律的熵表述仍然是成立的,然而开尔文表述需要进行修正2。
2. 负温度系统的条件
- 系统存在能量上限。那么当系统处于能量最高和能量最低状态时熵都为 $0$,因此这保证了 $S(E)$ 函数会存在斜率为负的部分。
- 负温度系统的内部相互作用弛豫时间要远小于系统与外部环境相互作用的弛豫时间。(例如在本文讨论的核自旋的例子中,自旋-自旋相互作用弛豫时间要远小于自旋-声子相互作用的弛豫时间)。
此外负温度系统为了保持稳定,需要满足平衡态稳定系统的熵判据,具体可以参考热动平衡判据文章。即
\begin{equation}
\,\mathrm{d}{S} =0, \,\mathrm{d}^{2}{S} <0~.
\end{equation}
其中第二个条件可以改写为
\begin{equation}
\frac{ \,\mathrm{d}^{2}{S} }{ \,\mathrm{d}{E} ^2}=\frac{ \,\mathrm{d}{}} { \,\mathrm{d}{E} }\left(\frac{1}{T}\right)<0~.
\end{equation}
也就是说,$-1/T$ 随着能量的增加而增加。换句话说,随着系统的能量增加,温度 $T$ 先是从 $0$ 增加到 $+\infty$,然后跳变到 $-\infty$,并从 $-\infty$ 逐渐增加到 $0$;这个过程中 $-1/T$ 单调递增,能量也单调递增。换句话说,$-1/T$ 是比通常的 $T$ 更加自然的能标。
3. 系综推导
子系(单个核构成的子系)的配分函数为
\begin{equation}
\begin{aligned}
Z=\sum_{\lambda}g_\lambda e^{-\beta \epsilon_\lambda}=e^{\beta \epsilon } +e^{-\beta \epsilon}~.
\end{aligned}
\end{equation}
利用近独立子系的热力学量表达式 式 2 和 式 10 ,可以由子系的配分函数得到系统的能量和熵的表达式:
\begin{equation}
\begin{aligned}
&\frac{\bar E}{N}=- \frac{\partial}{\partial{\beta}} \ln Z=-\frac{1}{Z} \frac{\partial Z}{\partial \beta}
=-\epsilon\frac{e^{\beta\epsilon}-e^{-\beta\epsilon}}{e^{\beta\epsilon}+e^{-\beta\epsilon}}~,\\
&\frac{S}{Nk}
=\ln Z-\beta \frac{\partial}{\partial{\beta}} \ln Z=
\ln \left(e^{\beta\epsilon}+e^{-\beta\epsilon}\right)-
\beta\epsilon \frac{e^{\beta\epsilon}-e^{-\beta\epsilon}}{e^{\beta\epsilon}+e^{-\beta\epsilon}}~.
\end{aligned}
\end{equation}
画出 $S$ 关于 $E$ 的函数曲线,可以得到类似于图 1 的结果,因此这里从系综的角度论证了负温度的出现。
1. ^ 参考玻尔兹曼分布(统计力学)或 热力学量的统计表达式(玻尔兹曼分布)的式 13 。
2. ^ 参考 Ramsey. 1956. PhysRev.103.20。
[1] ^ 汪志诚.热力学·统计物理 第五版
[2] ^ 林宗涵. 热力学与统计物理学 北京大学出版社 (2007)