贡献者: addis; _Eden_
回顾:函数是一个非空集合 $A$ 到另一个集合 $B$ 的对应法则。
本文中,函数 $f$ 是指从 $\mathbb R$ 的某个非空子集 $X$ 到 $\mathbb{R}$ 的映射
1. 函数的极限
图 1:请添加图片描述
定义 1 邻域和去心邻域
定义邻域为:$U(x_0,\delta)=\{x\in \mathbb{R}:|x-x_0|<\delta\}$.
定义去心邻域为:$U_0(x_0,\delta)= U(x_0,\delta) \backslash \{x_0\}=\{x\in \mathbb{R}:0<|x-x_0|<\delta\}$.
定义 2 极限
设函数 $f(x)$ 在 $U_0(x_0,\delta_0)$($\delta_0>0$)内有定义。
若存在实数 $A$,使得对任意 $\epsilon >0$,存在 $\delta>0$,使得当 $x\in U_0(x_0,\delta)$ 时,有 $|f(x)-A|<\epsilon$,则称当 $x$ 趋于 $x_0$,函数 $f(x)$ 以 $A$ 为极限,记为 $\large \lim\limits_{x\rightarrow x_0}f(x)=A$ 或 $f(x)\rightarrow A\ (x\rightarrow x_0)$。
补充:实际上有更宽泛的定义,只要 $x_0$ 是函数 $f(x)$ 定义域的聚点,就可以定义在该点处的极限。
同序列极限的性质类似,函数极限也具有唯一性:
定理 1
若函数 $f(x)$ 在 $x_0$ 处极限存在,证明在 $x_0$ 处极限唯一。
习题 1
- $f(x)=\left\{\begin{aligned} 0\ \ &(x<1)\\ 1\ \ &(x\ge 1) \end{aligned}\right.$,判断 $f(x)$ 在 $x_0=1$ 处极限是否存在。
- $f(x)=\left\{\begin{aligned} 0\ \ &(x<1)\\ 1\ \ &(x= 1)\\2\ \ &(x>1) \end{aligned}\right.$,判断 $f(x)$ 在 $x_0=1$ 处极限是否存在。
- $f(x)=x\cdot \sin\left(1/x\right) $,判断 $f(x)$ 在 $x_0=0$ 处极限是否存在。
- $f(x)= \sin\left(1/x\right) $,判断 $f(x)$ 在 $x_0=0$ 处极限是否存在。
- $f(x)= \mathrm{e} ^x$,证明 $\lim\limits_{x\rightarrow a}= \mathrm{e} ^a,\forall a\in\mathbb{R}$。
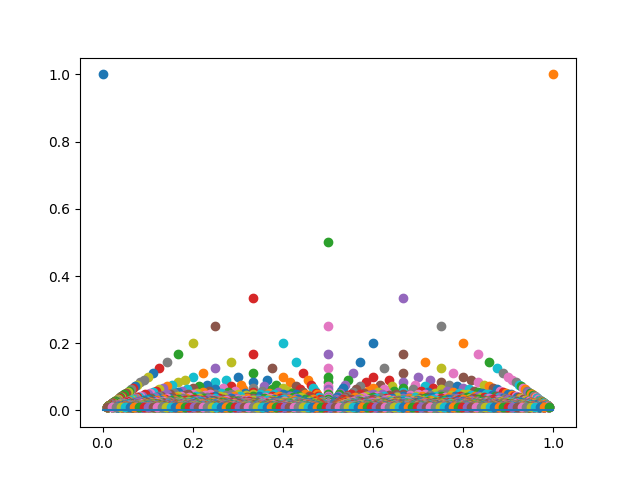
图 2:黎曼函数
我们来看一个有趣的函数 $f(x)$,它的定义域为 $[0,1]$:
\begin{equation}
f(x)=\left\{
\begin{aligned}
&1/q && (x=\frac{p}{q}\ (p,q\in \mathbb{N},\frac{p}{q}\text{为既约真分数}))\\
&0 && (\text{x=0 或 x=1 或 x}\notin \mathbb{Q})~.
\end{aligned}
\right.
\end{equation}
我们称它为
黎曼(Riemann)函数。
虽然在定义域内有无穷多个点的函数值不为 $0$,但 $f(x)$ 的极限却处处为 $0$,我们之后还将看到,$f(x)$ 在无理点处处连续,但 $f(x)$ 处处不可导。
习题 2
- 证明:若函数 $f(x)$ 在 $U(a,\delta_0)(\delta_0>0)$ 上有定义,且满足 $\large\lim\limits_{x\rightarrow a}f(x)=f(a)$,那么对任意极限为 $a$ 的序列 $\{x_n\}$,序列 $\{f(x_n)\}$ 的极限也为 $f(a)$。
上述命题反过来也成立。
- 对于任意给定的序列 $\{a_n\}(0< a_n<1)$,构造定义域为 $[0,1]$ 的函数 $f(x)$,满足 $\forall x\in \{a_n\},f(x)\neq 0;\ \forall x \in [0,1]\backslash \{a_n\},f(x)=0$,且 $f(x)$ 在定义域上极限处处为 $0$。
2. 函数的左右极限
图 3:请添加图片描述
如果把去心邻域 $U_0(x_0,\delta_0)$ 分成两块单侧邻域——
左空心邻域:$U_0^+(x_0,\delta)=U_0(x_0,\delta)\cap (x_0,+\infty) \{x\in \mathbb{R} :x_0< x< x_0+\delta\}~.$
右空心邻域:$U_0^-(x_0,\delta)=U_0(x_0,\delta)\cap (-\infty,x_0) \{x\in \mathbb{R} :x_0-\delta< x< x_0\}~.$
那么就可以定义函数的左右极限:
设 $f(x)$ 在 $U^+_0(x_0,\delta_0)(\delta_0>0)$ 上有定义。
如果存在实数 $A$,使得对任意 $\epsilon >0$,存在 $\delta>0$,当 $x\in U_0^+(x_0,\delta)$ 时,有 $|f(x)-A|<\epsilon$,则称 $f(x)$ 在点 $x_0$ 的右极限存在,而称 $A$ 为 $f(x)$ 在点 $x_0$ 的右极限,记为 $\lim\limits_{x\rightarrow x_0^+}f(x)=A$ 或 $f(x_0^+)=A$。
类似地可以定义左极限存在和左极限。
习题 3
- $f(x)=\left\{\begin{aligned} 0\ \ &(x<1)\\ 1\ \ &(x= 1)\\2\ \ &(x>1) \end{aligned}\right.$,判断 $f(x)$ 在 $x_0=1$ 处的左极限与右极限。
- $f(x)=[x]$(取整函数),判断 $f(x)$ 在 $x_0=1$ 处的左极限与右极限。
- 设函数 $f(x)$ 在 $U_0(x_0,\delta_0)$ 上有定义,证明:$\lim\limits_{x\rightarrow x_0} f(x)=A$ 当且仅当 $\lim\limits_{x\rightarrow x_0^-}f(x)=\lim\limits_{x\rightarrow x_0^+}f(x)=A$。
3. 函数极限的各种情况
称集合 $\{x:|x|>h\}(h>0)$ 为 $\infty$ 的邻域,记为 $U(\infty,h)$(这时就没有必要定义去心邻域了)。
同样的可以分成两块单侧邻域:
\begin{equation}
\begin{aligned}
&U^+(\infty,h)=U(\infty,h)\cup (0,\infty)=\{x:x>h\}~,\\
&U^-(\infty,h)=U(\infty,h)\cup (-\infty,0)=\{x:x<-h\}~.
\end{aligned}
\end{equation}
这样就可以函数在自变量趋向于无穷大时的极限:
设函数 $f(x)$ 在 $U^+(\infty,h_0)$ 上有定义。若存在实数 $A$,使得 $\forall \epsilon >0, \exists X\in U^+(\infty,h_0)$,当 $x>X$ 时,有 $|f(x)-A|<\epsilon$,则称当 $x$ 趋于 $+\infty$ 时 $f(x)$ 的极限存在,其极限为 $A$,记为 $\lim\limits_{x\rightarrow +\infty}f(x)=A$ 或 $f(x)\rightarrow A(x\rightarrow +\infty)$。
类似地可以定义 $\lim\limits_{x\rightarrow -\infty}f(x)=A$ 和 $\lim\limits_{x\rightarrow \infty}f(x)=A$。
习题 4
- 设函数 $f(x)$ 在 $U(\infty,h_0)$ 上有定义,证明:$\lim\limits_{x\rightarrow \infty} f(x)=A$ 当且仅当 $\lim\limits_{x\rightarrow -\infty}f(x)=\lim\limits_{x\rightarrow +\infty}f(x)=A$。
- 设序列 $\{a_n\}$ 收敛于 $A$,定义函数 $f(x)=a_{|[x]+1|}$,证明:$\lim\limits_{x\rightarrow \infty} f(x)=A$。
定义 3 广义极限
如果自变量趋向于一个值时,函数趋向于无穷大,则可以定义广义极限:
设 $f(x)$ 在 $U_0(x_0,\delta_0)(\delta_0>0)$ 上有定义,若 $\forall M>0,\exists \delta>0$,使得当 $x\in U_0(x,\delta)$ 时,有 $f(x)>M$,则称当 $x$ 趋于 $x_0$,$f(x)$ 趋于 $+\infty$,或称当 $x$ 趋于 $x_0$ 时,$f(x)$ 的广义极限为 $+\infty$。记为 $\lim\limits_{x\rightarrow x_0}f(x)=+\infty$ 或 $f(x)\rightarrow +\infty(x\rightarrow x_0)$。此时也称 $f(x)$ 为当 $x$ 趋于 $x_0$ 时的正无穷大量。
同样地可以定义负无穷大量和无穷大量。
对于函数极限而言,自变量有以下几种变化情况:
\begin{equation}
x\rightarrow x_0;\ x\rightarrow x_0^+;\ x\rightarrow x_0^{-};\ x\rightarrow \infty;\ x\rightarrow +\infty;\ x\rightarrow -\infty~.
\end{equation}
对于这六种情况可以定义各自的
广义极限:
\begin{equation}
f(x)\rightarrow A;\ f(x)\rightarrow +\infty;\ f(x)\rightarrow -\infty;\ f(x)\rightarrow \infty~,
\end{equation}
因此一共有 $24$ 种可能的函数极限的情形。
但由于它们之间有极大的相似之处,所以很容易进行记忆和想象。
习题 5
- $f(x)=x^2\sin x$,判断它是不是当 $x\rightarrow \infty$ 时的无穷大量。
- $f(x)=1/(x-1)\ (x\neq 1)$,求 $f(1^-),f(1^+),\lim\limits_{x\rightarrow 1}f(x),\lim\limits_{x\rightarrow \infty}f(x)$。