贡献者： DTSIo; _Eden_; addis; Giacomo
- 内容有重复，需要删减。单调收敛定理的内容与别的文章重叠，需要删减。
1. 基本定义解析
序列的极限是分析数学中最基本的定义。文章 数列的极限（简明微积分）和 极限 已经给出了一些序列极限的例子，它的形式定义以及背后的直观解释。为完整起见，这里再重复一次序列极限的定义：
定义 1 数列的极限
考虑数列 $\{a_n\}$。若存在一个实数 $A$，使得对于任意给定的正实数 $\varepsilon > 0$（无论它有多么小），总存在正整数 $N_\epsilon$，使得对于所有编号 $n>N_\varepsilon$，都有 $ \left\lvert a_n - A \right\rvert < \varepsilon$ 成立，那么数列 $a_n$ 的极限就是 $A$。
将 “数列 $\{a_n\}$ 的极限是 $A$” 表示为 $\lim\limits_{n\to\infty}a_n=A$。
正如之前两篇文章所解释的，等式 $\lim\limits_{n\to\infty}a_n=A$ 所表达的含义是"序列 $a_n$ 随着 $n$ 的增大将可以任意地接近 $A$". 或者说，对于序列 $\{a_n\}$ 进行极限运算，就是要找到"序列 $a_n$ 越来越接近的那个数". 这种运算显然跟实数的四则运算不一样。
有极限的序列常常称为收敛（convergent）的。如果没有极限，则序列称为发散（divergent）的。
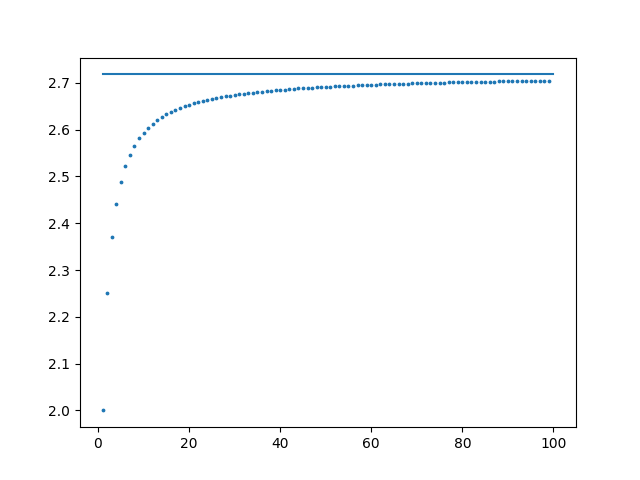
图 1：序列极限的示意图
例 1 求基本极限
证明$$\lim\limits_{n\to\infty}\frac{1}{2^n}=0~.$$
在给出严格证明之前，首先来看看序列 $\{2^{-n}\}$ 到底能够多么接近零。直观上，我们知道它衰减的速度非常快，例如第四项 $2^{-4}=0.0625$, 而第八项已经是 $2^{-8}=0.00390625$. 相比之下，倒数序列 $\{1/n\}$ 的第四项只是 $1/4=0.25$, 第八项只是 $1/8=0.125$. 因此，即便不借助对数运算，也可以说明序列 $\{2^{-n}\}$ 会逐渐接近于零。
转向严格证明。首先注意到初等的不等式 $2^n>n$ 对于任何整数 $n\geq1$ 都成立; 这可以使用数学归纳法得到。因此，给定一个误差 $\varepsilon>0$ 之后，要使得 $2^{-n}$ 同零的误差不大于 $\varepsilon$, 只需要 $1/n$ 同零的误差不大于 $\varepsilon$ 就够了，而为了达到这一点，只要 $n>1/\varepsilon$ 就够了。因此，只要取脚码
$$
N_\varepsilon=\left[\frac{1}{\varepsilon}\right]+1~,
$$
即可保证当 $n>N_\varepsilon$ 时有 $2^{-n}<\varepsilon$.
当然，直观上容易看出，序列 $\{2^{-n}\}$ 衰减得比倒数序列 $\{1/n\}$ 要快多了。上面的证明当然远远不是最精确的。为了刻画一个有极限的序列 $\{a_n\}$ 收敛的速度，可以考虑如下问题：给定了一个误差 $\varepsilon>0$ 之后，为了使得 $|a_n-A|<\varepsilon$ 能够一直成立，脚码 $n$ 至少得是多大？与此相关的概念正是无穷小的阶。
2. 基本性质
序列的极限运算有如下基本性质：
定理 1 极限的基本性质
- 序列的极限若存在，则必定是唯一的。
- 极限运算保持序关系：如果 $\lim\limits_{n\to\infty}a_n=A$, $\lim\limits_{n\to\infty}b_n=B$, 而且从某个 $n$ 开始有 $a_n\geq b_n$, 那么必然有 $A\geq B$.
- 设 $\lim\limits_{n\to\infty}a_n=A$, $\lim\limits_{n\to\infty}b_n=B$, 则序列 $\{a_n\pm b_n\}$ 和 $\{a_n b_n\}$ 都有极限，且 $\lim\limits_{n\to\infty}a_n\pm b_n=A\pm B$, $\lim\limits_{n\to\infty}a_nb_n=AB$.
- 设 $\lim\limits_{n\to\infty}a_n=A$, $\lim\limits_{n\to\infty}b_n=B\neq0$, 则
$$
\lim\limits_{n\to\infty}\frac{a_n}{b_n}=\frac{A}{B}~.
$$
例如我们在计算 $\{\frac{n+1}{n+2}\}$ 的极限时，可以将它拆成两个序列之和：$\{1\}$ 和 $\{-\frac{1}{n+2}\}$。容易证明第一个序列的极限为 $1$，第二个序列的极限为 $0$，那么两个序列之和的极限存在，且为 $1$。
下面我们将序列极限的性质一一道来。
定义 2 有界性
设 $\{x_n\}$ 是一个序列。若 $\exists M>0$，$\forall n$，有 $|x_n|\leq M$ 成立，则称 $\{x_n\}$ 是有界的。
显然以上定义等价于数集 $\{x_n\}$ 是一个有界集。
若一个序列 $\{x_n\}$ 是有界的，则记为 $x_n=O(1)\ (n\rightarrow \infty)$。若存在 $M_2>M_1>0$ 和正整数 $N$，使得当 $n>N$ 时，有 $M_1<|x_n|< M_2$，则以 $x_n=O_o(1)$ 表示之。
定理 2 收敛序列的有界性
- 收敛序列是有界的。
- 收敛序列的极限是唯一的。
以序列极限的唯一性为例，它可以用反证法来证明。假设收敛序列存在两个极限 $a$ 和 $b$，即 $\lim\limits_{n\rightarrow \infty}x_n=a$ 且 $\lim\limits_{n\rightarrow \infty} x_n=b$ 且 $a\neq b$。不失一般性，不妨设 $a< b$。现在取 $\epsilon_0=(b-a)/2$，则由极限定义知，存在正整数 $N_1$ 和 $N_2$，使得：
\begin{equation}
\begin{aligned}
|x_n-a|<\epsilon_0 \qquad &(\forall n>N_1)\\
|x_n-b|<\epsilon_0 \qquad &(\forall n>N_2)~.
\end{aligned}
\end{equation}
令 $N=\max\{N_1,N_2\}$，则当 $n>N$ 时，上述两个不等式都成立。那么
\begin{equation}
\begin{aligned}
&x_{N+1} < a+\epsilon_0=(a+b)/2~,\\
&x_{N+2} >b-\epsilon_0=(a+b)/2
\end{aligned}~
\end{equation}
导致矛盾。所以原命题成立。
定理 3 保序性
给定两个序列 $\{x_n\}$ 和 $\{y_n\}$，并且假定
\begin{equation}
\lim\limits_{n\rightarrow \infty} x_n=a~,\ \ \ \ \lim\limits_{n\rightarrow \infty} y_n = b,
\end{equation}
则有：
- 若 $a< b$，则对任意给定的 $c\in (a,b)$，$\exists N_0>0$，使得当 $n>N_0$ 时，有 $x_n< c< y_n$；
- 若 $\exists N_0>0$，当 $n>N_0$ 时，有 $x_n\leq y_n$，则 $a\leq b$。（注意逆命题不一定成立）
习题 1
构造两个序列 $\{x_n\},\{y_n\}$，使得 $\lim\limits_{n\rightarrow \infty}x_n\le \lim\limits_{n\rightarrow \infty} y_n$，但 $\forall n>0,x_n>y_n$。
定理 4 极限的四则运算
设 $\lim\limits_{n\rightarrow \infty} x_n=a,\ \lim\limits_{n\rightarrow \infty} y_n=b$，则
1. $\lim\limits_{n\rightarrow \infty}(x_n+y_n)=a+b,\ \ \lim\limits_{n\rightarrow \infty}(x_n-y_n)=a-b$；
2. $\lim\limits_{n\rightarrow \infty}(x_ny_n)=ab$；
3. $\lim\limits_{n\rightarrow \infty}(x_n/y_n)=a/b$，其中 $b\neq 0,\ y_n\neq 0$。
习题 2
若 $\lim\limits_{n\rightarrow \infty} x_n=1$；序列 $\{y_n\}$ 的元素是整数。那么序列 $\{x_n^{y_n}\}$ 的极限是否一定存在？请举一个 $\{x_n^{y_n}\}$ 的极限存在且不为 $1$ 的例子。
定理 5 夹逼收敛定理
设序列 $\{x_n\}$, $\{y_n\}$ 和 $\{z_n\}$ 满足 $x_n\leq z_n\leq y_n,\ \forall n>N_0$。
若 $\lim\limits_{n\rightarrow \infty}x_n=\lim\limits_{n\rightarrow \infty}y_n=a$，则 $\lim\limits_{n\rightarrow \infty}z_n=a$。
下面我们要介绍的是单调收敛原理。从直观上看，如果一个序列单调递增且不会趋于无穷大，那么它应该是有上确界的。其证明用到了确界存在定理。
定理 6 单调收敛原理
若序列 $\{x_n\}$ 单调递增且有上界，则序列收敛于 $\sup \{x_n\}$。
若序列 $\{x_n\}$ 单调递减且有下界，则序列收敛于 $\inf\{x_n\}$。
示意图如图 1 。
