贡献者: addis; JierPeter
简单来说,连续函数定义为:在某个区间内,函数曲线是连续的。例如常见的 $\sin x$,$\exp x$,$x^2$ 都在整个实数域上连续,又例如 $\ln x$ 和 $1/x$ 在区间 $(0, \infty)$ 上连续,$\tan x$ 在所有 $x_n = (1/2 + n)\pi$($n$ 为自然数)处不连续,$1/x$ 在 $x = 0$ 处不连续。但这只是一些简单的情况。在一些情况下这种判断方法则显得不严谨,例如函数
\begin{equation}
f(x) = \left\{\begin{aligned}
& \sin\left(1/x\right) \quad &(x \ne 0)\\
&0 \quad &(x = 0)
\end{aligned}\right. ~.
\end{equation}
在原点处的连续性(不连续)根据这个定义不好判断。所以我们需要一个更严谨的定义。
首先我们要讨论函数在一个点附近是否是连续的。这个概念的思想核心是,在函数曲线的某一点附近 $(x_0, f(x_0))$,无论我们要求 $f(x)$ 有多接近 $f(x_0)$,只要 $x$ 足够靠近 $x_0$,就一定能满足条件。比如说,如果定义函数 $f$ 为当 $x<0$ 的时候,$f(x)=0$,其它时候 $f(x)=1$,那么在 $x=0$ 这一点处 $f$ 就是跳跃的。如果我们要求的接近程度小于 $1$,那么无论 $x$ 多接近 $0$,只要 $x<0$,$f(x)$ 和 $f(0)=1$ 的距离就永远满足不了需要。
准确地描述以上 “连续” 的概念,如下所示:
定义 1 函数在一点的连续性和区间的连续性
函数 $f(x)$ 在某点 $x = x_0$ 处连续的定义是:函数 $f(x)$ 在某点 $x=x_0$ 处连续,当且仅当对于任何精度要求 $\epsilon>0$,我们都可以找到一个对应的范围 $\delta>0$,使得只要 $|x-x_0|<\delta$,就有 $|f(x)-f(x_0)|<\epsilon$。用极限符号来表示,就是:
\begin{equation}
\lim_{x \to x_0} f(x) = f(x_0)~.
\end{equation}
如果一个函数在某区间的所有点都连续,我们就说它在这个区间连续。
注意这里要求 $x$ 从左边和右边趋近于 $x_0$ 时的极限(即左极限和右极限)都成立。
1. 一致连续
以上所定义的连续性是针对一个个点 $x_0$ 而言的,就算函数在每一个点都连续,我们也只能说这个函数是逐点连续的(pointwise continuous)。事实上,还有一种更强的连续性,它着眼于整体的性质,这就是一致连续(uniformly continuous)。它的准确定义如下:
定义 2 一致连续
如果函数 $f(x)$ 在区间 $S$ 上,对于任意精度 $\epsilon>0$,都存在对应的范围 $\delta>0$,使得只要 $|x_1-x_2|<\delta$,那么 $|f(x_1)-f(x_2)|<\epsilon$。
一致连续着眼于整个区间的性质,而不是一个个点。显然,一致连续的函数肯定逐点连续,但是逐点连续的函数不一定一致连续,我们举一个反例。
例 1
例如考虑函数 $f(x)=1/x$,那么在区间 $(0, \infty)$ 上,$f$ 就是逐点连续的,但它并不一致连续;对于同样的精度要求 $\epsilon>0$ 和任何范围 $\delta>0$,只要 $0< x_1<\delta$,那么就总有一个足够小的 $x_2$ 使得 $|f(x_1)-f(x_2)|>\epsilon$,毕竟当 $x_2$ 接近 $0$ 的过程中,$f(x_2)$ 的斜率绝对值会趋近于无穷大。
习题 1 连续但不一致连续的函数
试证明 $1/x$ 在区间 $(0, +\infty]$ 以及 $x^2$ 在 $\mathbb R$ 都是连续的,但不是一致连续的。
定理 1
设 $S$ 是 $\mathbb{R}$ 的一个区间。函数 $f$ 在 $S$ 上逐点连续的充分必要条件是,对于任何开区间 $A\subset \mathbb{R}$,满足 $f(x)\in A$ 的所有 $x$ 构成的集合,是若干开区间的并集。用紧凑的写法来表达就是,$f^{-1}(A)$ 是开区间的并集。
这个定理还可以等价地用闭区间来表达:$f$ 在 $S$ 上逐点连续的充分必要条件是,任何闭区间的逆映射是闭区间的并集。
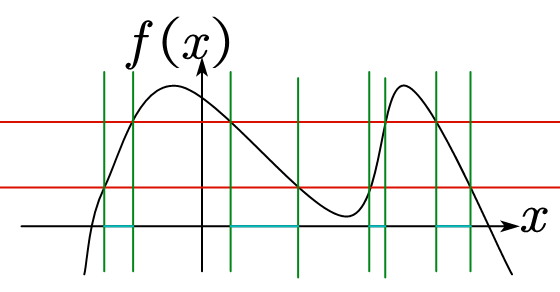
图 1:如图,红色水平线在 $f(X)$ 轴上划分出了一个开/闭区间,绿色垂直线是取反函数的过程,$x$ 轴上的靛蓝色线段就是取反函数的结果。从这个图可以直观地看出
定理 1 的意义。
在实数轴上,开集被定义为任何开区间的并集,而闭集是开集的补集。如果 $S$ 是 $\mathbb{R}$ 的一个子集,那么 $S$ 上的开集被定义为 $\mathbb{R}$ 的开集和 $S$ 的交集。这样一来,定理 1 就可以扩展为:$f$ 在 $S$ 上逐点连续,等价于对于任何开集 $A$,$f^{-1}(A)\cap S$ 是 $S$ 上的开集,等价于对于任何闭集 $B$,$f^{-1}(B)\cap S$ 是 $S$ 上的闭集。
用逆映射来刻画连续性是一个非常好用的方法。