惠斯通电桥
贡献者: addis
惠斯通电桥(Wheatstone bridge)也叫惠斯登电桥。(介绍未完成)
图 1:惠斯通电桥
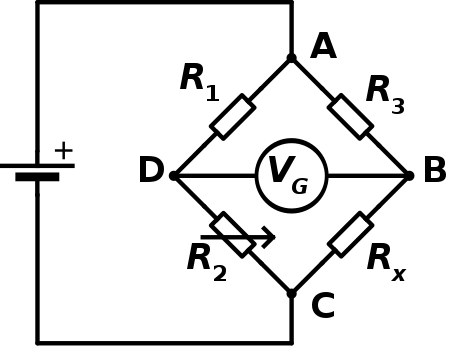
求电桥图 2 中电流计的电流 $I_G$ 与电源电动势及各臂电阻的关系(电源内阻可忽略)。
图 2:惠斯通电桥
选定各支路电流 $I_{1}, I_{2}, I_{3}, I_{4}, I_{\mathrm{G}}$ 及 $I $ 的正方向如图 2 中实箭头 所示。因节点数 $n = 4$,故可列出三个节点方程:
\begin{equation}
\begin{array}{ll}\text { 节点 } A: & I=I_{1}+I_{2}~, \\ \text { 节点 } B: & I_{1}=I_{3}+I_{G}~, \\ \text { 节点 } C: & I_{3}+I_{4}=I~.\end{array}
\end{equation}
\begin{equation}
\begin{array}{ll}\text { 回路 } \mathrm{I}: & I_{1} R_{1}+I_{\mathrm{G}} R_{\mathrm{G}}-I_{2} R_{2}=0~, \\ \text { 回路 } \mathrm{II}: & I_{3} R_{3}-I_{4} R_{4}-I_{\mathrm{G}} R_{\mathrm{G}}=0~, \\ \text { 回路 } \mathrm{III} : & I_{2} R_{2}+I_{4} R_{4}=\mathscr{E}~.\end{array}
\end{equation}
\begin{equation}
I_{\mathrm{G}}=\frac{\left(R_{2} R_{3}-R_{1} R_{4}\right) \mathscr{E}}{{R}_{1} R_{3}\left(R_{2}+R_{4}\right)+R_{2} R_{4}\left(R_{1}+R_{3}\right)+R_{\mathrm{G}}\left(R_{1}+R_{3}\right)\left(R_{2}+R_{4}\right)}~.
\end{equation}
\begin{equation}
R_{1} R_{4}=R_{2} R_{3}~.
\end{equation}