贡献者: 白玫瑰
1. 回顾
光的电磁理论认为,光是一种电磁波。电磁场的普遍规律可以总结为麦克斯韦方程组,积分形式的麦克斯韦方程组为:
\begin{equation}
\begin{aligned}
& \displaystyle \iint\!\!\!\!\!\!\!\!\!\!\subset\!\supset \boldsymbol{\mathbf{D}} \cdot \,\mathrm{d}{ \boldsymbol{\mathbf{\sigma}} } = Q ~, \\
& \displaystyle \iint\!\!\!\!\!\!\!\!\!\!\subset\!\supset \boldsymbol{\mathbf{B}} \cdot \,\mathrm{d}{ \boldsymbol{\mathbf{\sigma}} } = 0 ~, \\
& \oint \boldsymbol{\mathbf{E}} \cdot \,\mathrm{d}{ \boldsymbol{\mathbf{l}} } = - \iint \frac{\partial \boldsymbol{\mathbf{B}} }{\partial t} \,\mathrm{d}{ \boldsymbol{\mathbf{\sigma}} } ~, \\
& \oint \boldsymbol{\mathbf{H}} \cdot \,\mathrm{d}{ \boldsymbol{\mathbf{l}} } = \boldsymbol{\mathbf{I}} + \iint \frac{\partial \boldsymbol{\mathbf{D}} }{\partial t} \,\mathrm{d}{ \boldsymbol{\mathbf{\sigma}} } ~.
\end{aligned}
\end{equation}
方程组中,$ \boldsymbol{\mathbf{D}} $、$ \boldsymbol{\mathbf{E}} $、$ \boldsymbol{\mathbf{B}} $ 和 $ \boldsymbol{\mathbf{H}} $ 分别为电位移矢量、电场强度、磁感应强度和磁场强度,对 $ \,\mathrm{d}{ \boldsymbol{\mathbf{\sigma}} } $ 和 $ \,\mathrm{d}{ \boldsymbol{\mathbf{l}} } $ 的积分分别表示对电磁场中任一闭合曲面和闭合回路上的积分。$Q$ 为闭合曲面包含的总电量,$I$ 为闭合回路包围的传导电流1。方程组第 1 式为高斯定理,第 2 式表示磁场无源,第 3 式为法拉第电磁感应定律,第 4 式描述在电磁场中两种电流产生了磁场。
另有麦克斯韦方程组的微分形式:
\begin{equation}
\begin{aligned}
& \boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{\mathbf{D}} = \rho ~, \\
& \boldsymbol{\nabla}\boldsymbol{\cdot} \boldsymbol{\mathbf{B}} = 0 ~, \\
& \boldsymbol{\nabla}\boldsymbol{\times} \boldsymbol{\mathbf{E}} = -\frac{\partial \boldsymbol{\mathbf{B}} }{\partial t} ~, \\
& \boldsymbol{\nabla}\boldsymbol{\times} \boldsymbol{\mathbf{H}} = \boldsymbol{\mathbf{j}} + \frac{\partial \boldsymbol{\mathbf{D}} }{\partial t} ~.
\end{aligned}
\end{equation}
$\rho$ 为电荷体密度,$ \boldsymbol{\mathbf{j}} $ 为传导电流密度。
实际上,在方程组中,只有 $ \boldsymbol{\mathbf{E}} $ 和 $ \boldsymbol{\mathbf{B}} $ 是用于描述场的 “真正” 物理量,而 $ \boldsymbol{\mathbf{D}} $ 和 $ \boldsymbol{\mathbf{H}} $ 只是两个辅助量,$ \boldsymbol{\mathbf{E}} $ 和 $ \boldsymbol{\mathbf{D}} $、$ \boldsymbol{\mathbf{B}} $ 和 $ \boldsymbol{\mathbf{H}} $ 有着紧密联系,这一联系而电磁场所在的物质性质有关。
对于各向同性线性物质,我们有:
\begin{equation}
\begin{aligned}
& \boldsymbol{\mathbf{D}} = \varepsilon \boldsymbol{\mathbf{E}} ~, \\
& \boldsymbol{\mathbf{B}} = \mu \boldsymbol{\mathbf{H}} ~.
\end{aligned}
\end{equation}
$\varepsilon$ 和 $\mu$ 是两个标量,分别称为介电常数和磁导率。
对于各向异性物质,$\varepsilon$ 和 $\mu$ 不再是标量,而是 $n$ 阶张量:
\begin{equation}
\begin{aligned}
& \boldsymbol{\mathbf{D}} = \boldsymbol{\mathbf{\varepsilon}} \boldsymbol{\mathbf{E}} ~, \\
& \boldsymbol{\mathbf{B}} = \boldsymbol{\mathbf{\mu}} \boldsymbol{\mathbf{H}} ~.
\end{aligned}
\end{equation}
另外,我们有欧姆定律:
\begin{equation}
\begin{aligned}
\boldsymbol{\mathbf{j}} = \sigma \boldsymbol{\mathbf{E}} ~.
\end{aligned}
\end{equation}
$\sigma$ 被称为电导率。
式(3)和式(5)被称为物质方程。
变化的电磁场可以以一定速度向周围传播出去,即形成电磁波。我们有波动方程:
\begin{equation}
\begin{aligned}
& \boldsymbol{\nabla}^2 \boldsymbol{\mathbf{E}} - \frac{1}{v^2} \frac{\partial ^ 2 \boldsymbol{\mathbf{E}} }{\partial t^2} = 0 ~, \\
& \boldsymbol{\nabla}^2 \boldsymbol{\mathbf{B}} - \frac{1}{v^2} \frac{\partial ^ 2 \boldsymbol{\mathbf{B}} }{\partial t^2} = 0 ~.
\end{aligned}
\end{equation}
$ \boldsymbol{\mathbf{E}} $ 和 $ \boldsymbol{\mathbf{B}} $ 满足波动方程,即电场和磁场的传播是以波动形式进行的,传播速度为:
\begin{equation}
v = \frac{1}{\sqrt{\epsilon\mu}} ~.
\end{equation}
2. 光是一种电磁波
1889 年,赫兹在实验中得到了波长为 60cm 的电磁波,并且观察到电磁波在金属镜面上的反射与在石蜡棱镜中的折射及干涉现象。这一实验证明了电磁波的存在,也证明电磁波与光波的行为完全相同。
由(7)式,我们得到了电磁波在介质中的传播速度。由此,在真空中,电磁波的传播速度为:
\begin{equation}
c = \frac{1}{\sqrt{\epsilon_0 \mu_0}} ~.
\end{equation}
$\epsilon_0$ 和 $\mu_0$ 为真空中介电常数和磁导率。
通过计算,我们得到:
\begin{equation}
c = 2.99794 \times 10^8 m/s~.
\end{equation}
通过计算得到的这一数值,与实验中测得的真空中光速非常接近2,此为光是一种电磁波的又一有力证据。
3. 电磁波谱
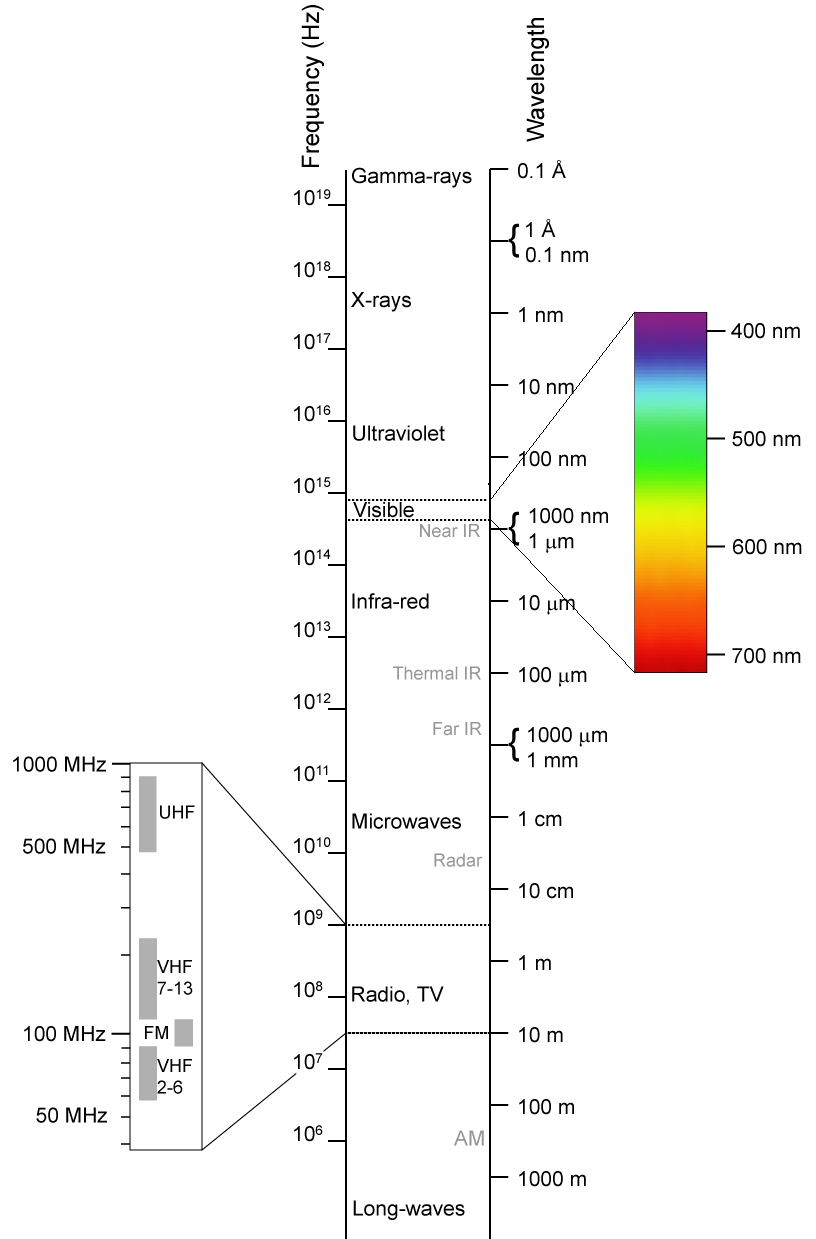
图 1:电磁波谱
我们所说的光学区或光学波谱,实际上指包括紫外线、可见光和红外线在内的波长范围(波长范围从 1nm 到 1mm)。可见光即人眼可感知到的各种颜色光波,波长范围在 390nm 到 780nm3。
4. 折射率
我们把光在真空中速度与介质中速度之比称为绝对折射率(简称折射率):
\begin{equation}
n = \frac{c}{v} ~.
\end{equation}
代入(7)式和(8)式,我们有:
\begin{equation}
n = \sqrt{\frac{\epsilon \mu}{\epsilon_0 \mu_0}} = \sqrt{\epsilon_r \mu_r} ~.
\end{equation}
$\epsilon_r$ 和 $\mu_r$ 即相对介电常数和相对磁导率:
\begin{equation}
\begin{aligned}
& \epsilon_r = \frac{\epsilon}{\epsilon_0} ~, \\
& \mu_r = \frac{\mu}{\mu_0} ~.
\end{aligned}
\end{equation}
除了磁性物质外,大多数物质 $\mu_r = 1$,则:
\begin{equation}
n = \sqrt{\epsilon_r} ~.
\end{equation}
1. ^ 想象一根闭合绳子捆着若干电线,这些电线都通有电流,你可以把传导电流简单理解为这些电流的总和
2. ^ $2.99792458m/s$,1983 年第 17 次国际计量大会将此数值作为真空中光速定义值
3. ^ 上述两个波长范围均指在真空中波长