双摆和三摆
贡献者: addis; FFjet
- 本文处于草稿阶段。
1. 双摆
图 1:双摆
运动方程
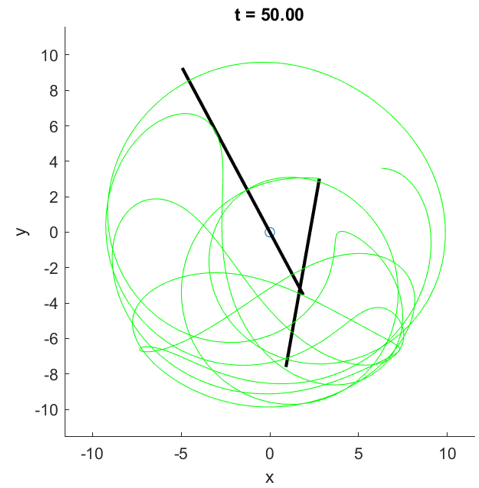
图 2:数值模拟结果,动画见这里,代码见 “双摆的数值计算(Matlab)”。
未完成:文字说明
$N$ 摆的动能可以参考这里。
\begin{equation}
\begin{aligned}
T &= \frac{1}{2} m_1 (l_1 \omega_1)^2 + \frac{1}{2} m_2 [(l_1 \omega_1 \cos\theta_1 + l_2 \omega_2 \cos\theta_2)^2 + (l_1 \omega_1 \sin\theta_1 + l_2 \omega_2 \sin\theta_2)^2]~,
\end{aligned}
\end{equation}
\begin{equation}
V = -m_1 g l_1 \cos \theta_1 - m_2 g (l_1\cos \theta_1 + l_2 \cos \theta_2)~,
\end{equation}
\begin{equation}
L(\theta_1, \theta_2, \omega_1, \omega_2) = T(\omega_1, \omega_2) - V(\theta_1, \theta_2)~,
\end{equation}
\begin{equation}
\frac{\mathrm{d}}{\mathrm{d}{t}} \frac{\partial L}{\partial \omega_i} = \frac{\partial L}{\partial \theta_i} \quad (i=1,2)~.
\end{equation}
令 $\alpha = \theta_2-\theta_1$,得
\begin{equation}
\frac{\partial T}{\partial \omega_1} = (m_1 + m_2)l_1^2\omega_1 + m_2l_1l_2\cos\alpha\cdot\omega_2~,
\end{equation}
\begin{equation}
\frac{\partial T}{\partial \omega_2} = m_2l_1l_2\cos\alpha\cdot\omega_1 + m_2l_2^2\omega_2~,
\end{equation}
\begin{equation}
\frac{\mathrm{d}}{\mathrm{d}{t}} \frac{\partial T}{\partial \omega_1} = (m_1 + m_2)l_1^2\dot\omega_1 + m_2l_1l_2\cos\alpha\cdot\dot\omega_2 - m_2l_1l_2\sin\alpha(\omega_2-\omega_1)~,
\end{equation}
\begin{equation}
\frac{\mathrm{d}}{\mathrm{d}{t}} \frac{\partial T}{\partial \omega_2} = m_2l_1l_2\cos\alpha\cdot\dot\omega_1 + m_2l_2^2\dot\omega_2 -m_2l_1l_2\sin\alpha(\omega_2-\omega_1)\omega_1~,
\end{equation}
\begin{equation}
\frac{\partial T}{\partial \theta_1} = m_2l_1l_2\sin\alpha\cdot \omega_1\omega_2~,
\end{equation}
\begin{equation}
\frac{\partial T}{\partial \theta_2} = -m_2l_1l_2\sin\alpha\cdot \omega_1\omega_2~,
\end{equation}
\begin{equation}
\frac{\partial V}{\partial \theta_1} = m_1gl_1\sin\theta_1 + m_2gl_1\sin\theta_1~,
\end{equation}
\begin{equation}
\frac{\partial V}{\partial \theta_2} = m_2gl_2\sin\theta_2~.
\end{equation}
\begin{equation}
(m_1+m_2)l_1\dot\omega_1 + m_2l_2\cos\alpha\cdot\dot\omega_2 = m_2l_2\sin\alpha\cdot\omega_2^2 - (m_1+m_2)g\sin\theta_1~,
\end{equation}
\begin{equation}
l_1\cos\alpha\cdot\dot\omega_1 + l_2\dot\omega_2 = l_1 \sin\left(\theta_1-\theta_2\right) \omega_1^2 - g\sin\theta_2~,
\end{equation}
\begin{equation}
\dot\omega_1 = \frac{m_2l_2\sin\alpha\cdot\omega_2^2 - (m_1+m_2)g\sin\theta_1 + m_2[l_1\sin\alpha\cdot\omega_1^2 + g\sin\theta_2] \cos\alpha}{m_1l_1 + m_2l_1\sin^2\alpha}~,
\end{equation}
\begin{equation}
\dot\omega_2 = \frac{[(m_1+m_2)g\sin\theta_1 - m_2l_2\sin\alpha\cdot\omega_2^2]\cos\alpha - (m_1+m_2)[l_1\sin\alpha\cdot\omega_1^2 + g\sin\theta_2]}{m_1l_2 + m_2l_2\sin^2\alpha}~.
\end{equation}
2. 刚体双摆
图 3:刚体双摆的模拟结果,动画见这里,代码见 “双摆的数值计算(Matlab)”。
若第一个质量为 $m_1$ 刚体的质心用 $l_1,\theta_1$ 描述,关于质心的转动惯量为 $I_1$,第二个刚体质量为 $m_2$,转轴与第一个刚体的转轴距离 $r_1$,与第一个刚体质心的夹角为 $\alpha$,那么
\begin{equation}
\begin{aligned}
T &= \frac{1}{2}m_1 l_1^2 \omega_1^2 + \frac{1}{2}I_1 \omega_1^2
+ \frac{1}{2}m_2[(r_1\omega_1 \cos\left(\theta_1 + \alpha\right) + l_2\omega_2\cos\theta_2)^2\\
&\qquad \qquad \qquad+ (r_1\omega_1 \sin\left(\theta_1+\alpha_1\right) + l_2\omega_2\sin\theta_2)^2] + \frac{1}{2}I_2\omega_2^2\\
&= \frac{1}{2}(m_1l_1^2 + m_2r_1^2 + I_1)\omega_1^2 + \frac{1}{2}(m_2l_2^2 + I_2)\omega_2^2 + m_2r_1l_2 \cos\left(\theta_1+\alpha-\theta_2\right) \omega_1\omega_2~,
\end{aligned}
\end{equation}
\begin{equation}
V = -m_1 g l_1 \cos \theta_1 - m_2 g (r_1 \cos\left(\theta_1 + \alpha\right) + l_2 \cos \theta_2)~.
\end{equation}
\begin{equation}
\frac{\mathrm{d}}{\mathrm{d}{t}} \frac{\partial T}{\partial \omega_1} = 2a\dot\omega_1 + c\dot\omega_2 + \frac{\partial c}{\partial \theta_1} \omega_1\omega_2 + \frac{\partial c}{\partial \theta_2} \omega_2^2~,
\end{equation}
\begin{equation}
\frac{\mathrm{d}}{\mathrm{d}{t}} \frac{\partial T}{\partial \omega_2} = 2b\dot\omega_2 + c\dot\omega_1 + \frac{\partial c}{\partial \theta_1} \omega_1^2 + \frac{\partial c}{\partial \theta_2} \omega_1\omega_2~,
\end{equation}
\begin{equation}
\frac{\partial T}{\partial \theta_1} = \frac{\partial c}{\partial \theta_1} \omega_1\omega_2, \qquad
\frac{\partial T}{\partial \theta_2} = \frac{\partial c}{\partial \theta_2} \omega_1\omega_2~,
\end{equation}
\begin{equation}
\frac{\partial V}{\partial \theta_1} = m_1gl_1\sin\theta_1 + m_2gr_1 \sin\left(\theta_1+\alpha\right) , \qquad
\frac{\partial V}{\partial \theta_2} = m_2gl_2\sin\theta_2~.
\end{equation}
\begin{equation}
2a\dot\omega_1 + c\dot\omega_2 = - \frac{\partial c}{\partial \theta_2} \omega_2^2 - \frac{\partial V}{\partial \theta_1} ~,
\end{equation}
\begin{equation}
c\dot\omega_1 + 2b\dot\omega_2 = - \frac{\partial c}{\partial \theta_1} \omega_1^2 - \frac{\partial V}{\partial \theta_2} ~,
\end{equation}
3. 三摆
图 4:三摆
如图 4 所示,三根质量不计的杆长度分别为 $l_1, l_2, l_3$,三个质点的质量分别为 $m_1, m_2, m_3$。我们把这个模型叫做三摆。三摆常用于演示物理学中的混沌现象。
运动方程
未完成:文字说明
\begin{equation}
\begin{aligned}
T &= \frac{1}{2} m_1 (l_1 \omega_1)^2 + \frac{1}{2} m_2 [(l_1 \omega_1 \cos\theta_1 + l_2 \omega_2 \cos\theta_2)^2 +\\
&\qquad \qquad\qquad\qquad\qquad\qquad (l_1 \omega_1 \sin\theta_1 + l_2 \omega_2 \sin\theta_2)^2]\\
& + \frac{1}{2} m_3 [(l_1 \omega_1 \cos\theta_1 + l_2 \omega_2 \cos\theta_2 + l_3 \omega_3 \cos \theta_3)^2 +\\
&\qquad\qquad\qquad (l_1 \omega_1 \sin\theta_1 + l_2 \omega_2 \sin\theta_2 + l_3 \omega_3 \sin\theta_3)^2]~.
\end{aligned}
\end{equation}
\begin{equation}
\begin{aligned}
V &= -m_1 g l_1 \cos \theta_1 - m_2 g (l_1\cos \theta_1 + l_2 \cos \theta_2)\\
&\qquad - m_3 g (l_1 \cos\theta_1 + l_2 \cos \theta_2 + l_3 \cos \theta_3)~.
\end{aligned}
\end{equation}
\begin{equation}
L(\theta_1, \theta_2, \theta_3, \omega_1, \omega_2, \omega_3) = T(\omega_1, \omega_2, \omega_3) - V(\theta_1, \theta_2, \theta_3)~.
\end{equation}
\begin{equation}
\frac{\mathrm{d}}{\mathrm{d}{t}} \frac{\partial L}{\partial \omega_i} = \frac{\partial L}{\partial \theta_i} \quad (i=1,2,3)~.
\end{equation}
这是一个二阶微分方程组。